 |
Inhalt • Suchen |  |
2020-09-07
Wege
Wie berechnet man die Wahrscheinlichkeit, dass ein bestimmtes Ereignis eintritt? Am Beispiel des jedem bekannten Würfelns lässt sich das recht einfach erklären.
Ein Würfel hat sechs Seiten, auf denen er zum Liegen kommen kann, wenn man ihn wirft. Für unser Beispiel gehe ich davon aus, dass der Würfel ein idealer Würfel ist, d. h. alle seine Ecken sind exakt gleich abgerundet, sein Schwerpunkt befindet sich genau in der Mitte, etc. Wenn man nun auch noch den Wurf so durchführt, dass ausgeschlossen werden kann, dass seine Wurfbahn in irgendeiner Weise vorherbestimmt wird (z. B. indem man den Würfel vor dem Wurf in einem Becher einige Male kräftig schüttelt), dann haben wir alle Voraussetzungen geschaffen, dass keine der sechs Seiten in irgendeiner Weise bevorteilt wird.
Die Wahrscheinlichkeit, dass ein bestimmtes Ergebnis eintritt, ist stets das Verhältnis aller möglichen Ergebnisse zur Anzahl der günstigen Ergebnisse.
Die Anzahl aller möglichen Ergebnisse ist bei einem Würfel stets 6, da er auf jeder der 6 Seiten zum Liegen kommen kann. Wenn ich nun nach der Wahrscheinlichkeit frage, dass ich bei einem Wurf eine 4 erhalte, dann ist die Anzahl der günstigen Ergebnisse 1 (nur eine 4 wird als günstig gewertet, alle anderen Ergebnisse als ungünstig), somit ist die zu berechnende Wahrscheinlichkeit
| P = |
|
= |
|
≈ | 0,1667 |
wobei P die Wahrscheinlichkeit ist (P ist die allg. übliche Bezeichnung, sie steht für das englische Probability = Wahrscheinlichkeit), Ng ist die Anzahl der günstigen Ergebnisse und Nm ist die Anzahl der möglichen Ergebnisse.
Betrachten wir nun einen etwas anderen Fall: Ich lasse eine Kugel auf einen Nagel fallen, der in ein Brett geschlagen ist. Das Brett steht senkrecht, der Nagel ragt waagrecht daraus hervor:

Lasse ich die Kugel genau auf die Mitte des Nagels fallen, dann hat sie zwei Möglichkeiten zum weiteren Herunterfallen: links oder rechts. Die Wahrscheinlichkeit, dass sie links hinunterfällt, ist
|
und auch die Wahrscheinlichkeit, dass sie rechts vom Nagel hinunterfällt, ist
|
Das leuchtet ein und ist alles, was wir für das nächste Experiment wissen müssen. Wir basteln uns jetzt nämlich ein sogenanntes Galton-Brett.1) Dafür verwenden wir unser oben skizziertes Brett und schlagen unterhalb des bereits vorhandenen Nagels weitere Nägel ein – auf folgende Weise:
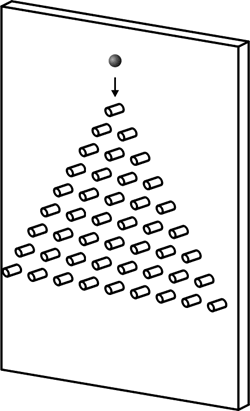
Lasse ich die Kugel nun wieder genau auf die Mitte des oberen Nagels fallen, wird sie wie vorhin mit einer Wahrscheinlichkeit von jeweils
|
entweder auf den links darunter befindlichen oder den rechts darunter befindlichen Nagel fallen. Von diesem Nagel aus wird sie wiederum mit einer Wahrscheinlichkeit von jeweils
|
auf einen der nächsten Nägel in der darunterliegenden Reihe fallen und so weiter. Wo wird die Kugel nun unten ankommen? Das wissen wir nicht. Allerdings können wir eines tun: Wir können die Wahrscheinlichkeiten für jeden Ort berechnen, auf den sie fallen kann. Wir machen das, indem wir für jeden einzelnen Nagel die Wahrscheinlichkeit, dass die Kugel dort auftrifft, berechnen.
Die Wahrscheinlichkeit, dass die Kugel auf den obersten Nagel trifft, ist genau 1. Denn die Kugel fällt mit Sicherheit dorthin, sie hat gar keine andere Möglichkeit. In der zweiten Reihe trifft sie – das wissen wir bereits – mit einer Wahrscheinlichkeit von jeweils
|
auf einen der beiden dort befindlichen Nägel. In der dritten Reihe gibt es nun bereits mehrere Möglichkeiten. Um diese zu verdeutlichen, bezeichne ich die Nägel der ersten drei Reihen mit Buchstaben:
| A | ||||
| ● | ||||
| B | C | |||
| ● | ● | |||
| D | E | F | ||
| ● | ● | ● |
Die Wahrscheinlichkeiten für das Auftreffen auf einen Nagel betragen nun
| A | = |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| B = |
|
C = |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
| D = |
|
⋅ |
|
= |
|
E = |
|
⋅ |
|
+ |
|
⋅ |
|
= |
|
F = |
|
⋅ |
|
= |
|
|||||||||||||||||||||||||||||||||||||
Der Nagel E tanzt ein wenig aus der Reihe. Hier addieren sich nämlich zwei verschiedene mögliche Wege, welche die Kugel nehmen kann: Ein Weg führt über den Nagel B und ein anderer Weg über den Nagel C. Wir müssen nämlich alle möglichen Wege berücksichtigen. Für die weiter darunter liegenden Reihen wird die Anzahl der möglichen Wege immer größer.
Diese kann man in eine Tabelle eintragen. Aufgrund der dreiecksförmigen Anordnung der Nägel zeichne ich sie in sechseckige Waben ein:
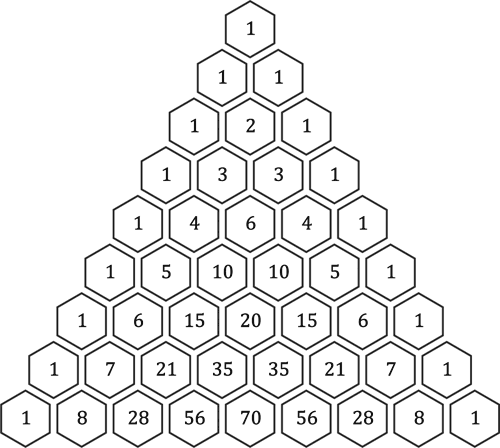
Jenen, die »Werden« gelesen haben, wird dieses Muster bekannt vorkommen. Wer aufmerksam ist, erkennt sofort das Pascal’sche Dreieck! Überprüfen wir, ob hier auch tatsächlich eine Übereinstimmung vorliegt. Ich wähle einige Nägel aus und betrachte alle möglichen Wege, die dorthin führen:
Der Nagel in der stark umrandeten Wabe trägt die Zahl 3 – und tatsächlich führen genau 3 mögliche Wege dort hin:

Ein weiterer Nagel in der nächsten Reihe trägt die Zahl 4:

Der Nagel daneben in der Mitte trägt die Zahl 6 – und auch hier stimmt die Zahl der möglichen Wege wieder überein:

Das Pascal’sche Dreieck zeigt tatsächlich in jedem Punkt genau die Anzahl aller möglichen Wege im Galton-Brett.
Was passiert nun, wenn wir viele Kugeln nacheinander auf den obersten Nagel fallen lassen und die einzelnen Ziele, in denen die Kugeln landen, aufzeichnen? Genau das hat Francis Galton mit dem nach ihm benannten Brett gemacht. Er hat zu diesem Zweck unterhalb des Nagel-Dreiecks die Kugeln so aufgefangen, dass er sie anschließend getrennt zählen konnte. Die Konstruktion sieht, von vorne betrachtet, in etwa so aus:
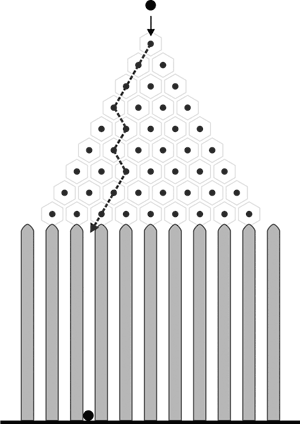
Die erste Kugel hat einen der möglichen Wege genommen und ist in einem Sammelschacht gelandet. Weitere Kugeln könnten z. B. so zu liegen kommen:
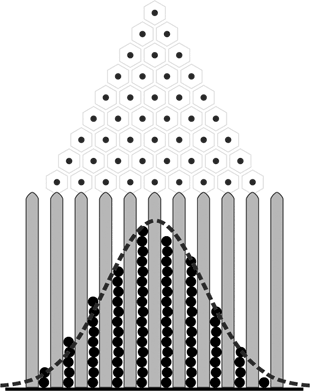
Das Bild zeigt ein mögliches Ergebnis mit einer größeren Menge Kugeln. Die mittleren Schächte enthalten mehr Kugeln als die weiter außen liegenden. Das war auch zu erwarten, denn schließlich führen zu den mittleren Schächten mehr Wege als zu den außen liegenden Schächten und entsprechend höher ist die Wahrscheinlichkeit, dass eine Kugel im mittleren Bereich zu liegen kommt. Die dicke strichlierte Linie ist eine sogenannte Gaußsche Glockenkurve,2) auch Normalverteilungskurve genannt (genauer: Dichtefunktion der Normalverteilung).
Diese Glockenkurve erhält man, wenn man die Zahlen einer Zeile im Pascalschen Dreieck glättet. Die geglättete Kurve kann über die Formel
| 1 |
  2π 2π
|
| x2 | ||
| 2 |
berechnet werden. Genau genommen gibt es im gesamten Universum aber keine »glatte« Wahrscheinlichkeit für irgendein Ereignis, da alle Ereignisse das Ergebnis aus einer Kombination von Einzelereignissen (also einer ganzzahligen Anzahl von Ereignissen) sind. Nichts im Universum ist »glatt«. Alles besteht, wenn man möglichst genau hinsieht, aus einzelnen »Teilchen«, auch »Quanten« genannt. Der Begriff »möglichst genau« deutet darauf hin, dass ein »ganz genau« nicht möglich ist. Werner Heisenberg hat das herausgefunden.
Physiker haben auch herausgefunden, dass jedes einzelne Quanten-Ereignis dem Zufall unterliegt und nicht berechnet werden kann – berechnen lässt sich nur die Wahrscheinlichkeit seines Eintretens. Jedes(!) Quanten-Ereignis, welcher Form auch immer, ist zufällig. Warum es zufällig ist, kann aber niemand erklären. Die Ursache des Zufalls kennt niemand.
Eine Voraussetzung für die Berechnung einer Wahrscheinlichkeit, die normalverteilt ist, ist die Unabhängigkeit der einzelnen Ereignisse voneinander. Das heißt im Fall des Würfelns, dass jeder einzelne Wurf die gleichen Voraussetzungen hat wie alle anderen Würfe und dass das Ergebnis der bereits erfolgten Würfe auf die Voraussetzungen für die nachfolgenden Würfe keinerlei Einfluss hat.
Gleiches gilt natürlich für das Galton-Brett. Auch hier muss jede Kugel, die auf den ersten Nagel fällt, die gleichen Voraussetzungen haben wie alle anderen Kugeln, die bereits in einem der Schächte liegen.
Die Genauigkeit, mit der die Wahrscheinlichkeit einzelner Ereignisse gemessen werden kann, steigt mit der Anzahl der Ereignisse. Wenn ich nur 5 Einzel-Ereignisse messe, dann bekomme ich ein Ergebnis, das kaum etwas über die tatsächliche Verteilung aussagt. Beispielsweise kann es durchaus vorkommen, dass beim Fall von 5 Kugeln auf das Galton-Brett 4 Kugeln im Schacht 2 landen und eine Kugel im Schacht 3 – bei insgesamt 10 Schächten wie in unserer Beispielgrafik. Das Ergebnis ähnelt natürlich ganz und gar nicht einer symmetrischen Glockenkurve. Verwende ich jedoch 500 Kugeln und es landen davon 400 im Schacht 2 und 100 im Schacht 3, dann weiß ich mit extrem hoher Sicherheit, dass mit dem Brett etwas faul ist – jedem Menschen leuchtet das intuitiv ein.
Normalverteilungen findet man in der uns bekannten Welt so gut wie überall. Eine Normalverteilungskurve wie die Gaußsche Glockenkurve ist aber eine idealisierte (geglättete) Linie. Die tatsächliche Kurve ist treppenförmig und entspricht einer Binomialverteilung – diese wiederum wird immer genauer identisch mit der idealisierten Glockenkurve, je mehr Einzelereignisse berücksichtigt werden. In der von uns erlebten Welt können wir so gut wie immer die glatte Glockenkurve verwenden, wenn wir zufällig stattfindende Ereignisse berechnen wollen, da die kleinen Treppenstufen der tatsächlich zugrundeliegenden Kurve so winzig sind, dass wir sie nicht einmal mit dem stärksten Mikroskop sehen können. Wir können sie nicht einmal theoretisch sehen. Denn sie unterliegen der Heisenbergschen Unschärfe. Im ganz Kleinen, auf der Ursachenebene, verschwimmt die Welt vor unseren Augen. Mit den Mitteln der äußeren Welt, der 4-dimensionalen Welt, können wir hier nichts ausrichten.
Später werde ich genauer auf diese Unschärfe eingehen, denn sie gehört zum Wichtigsten überhaupt, wenn wir die Entstehung von Materie verstehen wollen. Für heute soll für uns im Gedächtnis hängen bleiben: Zufall hat mit der Anzahl der möglichen Wege zu tun. Jedes Quanten-Ereignis, also jedes Einzel-Ereignis auf der absolut kleinsten Skala dessen, was wir noch erfassen können, ist dem Zufall unterworfen. Und somit einer bestimmten Wahrscheinlichkeit seines Eintreffens. Wir brauchen uns nur zu merken: Die Wahrscheinlichkeit, dass ein Ereignis eintritt, ist das Verhältnis der günstigen Ereignisse zu allen möglichen Ereignissen.
Immer, wenn wir die Wahrscheinlichkeit des Eintretens eines Ereignisses berechnen wollen, müssen wir vorher berechnen, wieviele Möglichkeiten es gibt, dass es eintreten kann.
Ich mache nun etwas sehr Sonderbares. Ich will herausfinden, wieviele Möglichkeiten es gibt, eine ganze Zahl aus einfachen Potenzen von Φ zu bilden. Wer Werden gelesen hat, der weiß, dass jede ganze Zahl prinzipiell auf unendlich viele Weisen durch Potenzsummen von Φ gebildet werden kann. Es gibt somit unendlich viele Möglichkeiten. Und gleichzeitig gibt es nur eine einzige Möglichkeit für jede beliebige ganze Zahl, sie in einem Φ-System so darzustellen, dass keine Stelle im Φ-System direkt neben einer anderen zu liegen kommt, dass also der »Mindest-Abstand« von 1 zwischen den Potenzen an jeder Stelle eingehalten wird. Diese Variante bildet jeweils die »Ideal-Form« einer ganzen Zahl. Zur Erinnerung: Die Idealform der ersten 30 ganzen Zahlen in einem Φ-System sieht so aus:
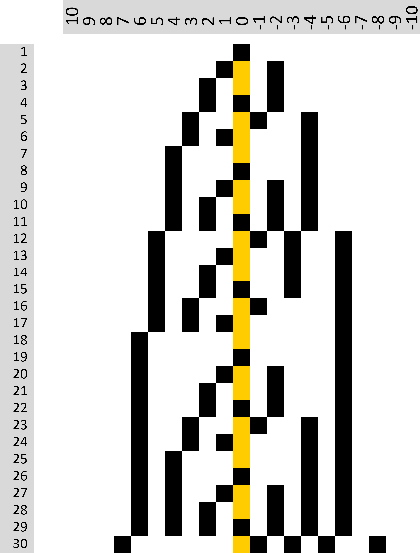
Die Idealform enthält stets eine kleinste Stelle, deren Potenzwert entweder gleich oder um maximal 1 kleiner ist als der Potenzwert an der größten Stelle. Der kleinste und der größte Potenzwert bilden sozusagen die »Hülle« für die Stellen innerhalb des Körpers einer ganzen Zahl. Die Dezimalzahl 15 setzt sich in ihrer Idealform aus den Φ-Potenzen +5, +2, 0, −3 und −6 zusammen. Mathematisch ausgedrückt:
1510 = Φ5 + Φ2 + Φ0 + Φ−3 + Φ−6 = 100101,001001Φ
Da wir wissen, dass Φn = Φn − 1 + Φn − 2, können wir die Dezimalzahl 15 auch auf die folgenden Weisen hinschreiben:
| 1510 = Φ5 + Φ2 + Φ0 + Φ−3 + Φ−7 + Φ−8 | = | 100101,00100011Φ |
| 1510 = Φ5 + Φ2 + Φ0 + Φ−3 + Φ−7 + Φ−9 + Φ−10 | = | 100101,0010001011Φ |
| 1510 = Φ5 + Φ2 + Φ0 + Φ−3 + Φ−7 + Φ−9 + Φ−11 + Φ−12 | = | 100101,001000101011Φ |
| 1510 = Φ5 + Φ2 + Φ0 + Φ−3 + Φ−7 + Φ−9 + Φ−11 + Φ−13 + Φ−14 | = | 100101,00100010101011Φ |
usw.
Die »rechte Seite der Hülle« kann stets bis ins Unendliche ausgedehnt werden. Alle anderen Zahlensysteme, die auf ganzen Zahlen basieren (Dualsystem, Dezimalsystem, ...) bieten diese Möglichkeit nicht. Hier ist jede ganze Zahl nur auf eine einzige Weise exakt schreibbar. 15 kann ich im Dezimalsystem nur auf diese Weise schreiben:
1510 = 1⋅101 + 5⋅100
Im Dualsystem gibt es ebenfalls nur eine einzige Möglichkeit, die Dezimalzahl 15 aufzuschreiben:
1510 = 11112 = 23 + 22 + 21 + 20
Ganzzahlige Stellenwertsysteme bieten keinen »Zwischenraum«, um andere Schreibweisen zu ermöglichen. Bei einem Φ-System ist das anders. Die Dezimalzahl 15 kann ich zwar nur auf eine Weise in ihrer Idealform schreiben (sodass zwischen allen Stellen der Mindestabstand von 1 gewahrt bleibt), aber wenn irgendwo eine Lücke zwischen den Stellen ist, die größer als 1 ist, dann habe ich hier die Möglichkeit, eine andere Schreibweise einzuschieben, ohne die »Hülle« auszudehnen. Schauen wir uns die Zahl 15 im Φ-System genauer an:

Wir sehen, dass es hier insgesamt 3 Lücken gibt, die größer als 1 sind, nämlich zwischen den Potenzen 5 und 2, 0 und –3, sowie zwischen –3 und –6. Daher können wir die Zahl 15 im Φ-System innerhalb der Hülle des Zahlenkörpers auch auf folgende Weisen schreiben:

In den Zeilen A bis F habe ich alle 6 möglichen Kombinationen, die sich aus den 3 Lücken ergeben, aufgezeichnet. Wenn man sich das Ergebnis genau anschaut, dann entdeckt man, dass in den Zeilen B, D und F jeweils eine Lücke zu sehen ist, die neu ist, da sie erst dadurch entstanden ist, indem ich den Potenzwert an der Stelle 0 durch die Potenzen an den Stellen –1 und –2 ersetzt habe. Wenn ich das berücksichtige und jeweils wieder mit allen anderen Möglichkeiten kombiniere, so werde ich feststellen, dass es insgesamt 12 Möglichkeiten gibt, die Dezimalzahl 15 innerhalb der »optimalen Hülle« darzustellen.
Für größere Zahlen ist zu vermuten, dass es mehr Möglichkeiten geben sollte als für kleinere Zahlen. Dies trifft jedoch nur tendenziell zu, denn es gibt auch Zahlen, die keine einzige Lücke aufweisen, die größer als 1 ist! Nehmen wir als Beispiel die Dezimalzahl 11. Diese sieht im Φ-System wie folgt aus:
1110 = Φ4 + Φ2 + Φ0 + Φ−2 + Φ−4 = 10101,0101Φ
Hier gibt es nur Lücken, die eine Breite von genau 1 haben. Somit ist die Dezimalzahl 11 nur auf genau eine einzige Weise innerhalb der optimalen Hülle darstellbar.
Wie sieht das nun im gegenteiligen Fall aus? Wie muss eine Zahl im Φ-System beschaffen sein, damit möglichst viele Kombinationen innerhalb ihrer Hülle Platz finden, und wie groß ist das Maximum dieser Möglichkeiten?
Ich habe eine ganze Woche damit verbracht, das herauszufinden. Kombinatorik ist eine nicht ganz einfache Kunst – jedenfalls empfand ich das so, da ich in den ersten Tagen versucht habe, mit Formeln aus dem Gebiet der Kombinatorik die Fragen zu beantworten. Dabei bin ich gehörig ins Schwitzen gekommen ... Wenn man allerdings sehr genau, akribisch und sorgfältig an die Sache herangeht, dann fallen die meisten Schwierigkeiten ganz von selber ab. Ich habe im Anschluss sogar eine einfach zu bedienende Software geschrieben, mit deren Hilfe man online sämtliche Möglichkeiten berechnen und grafisch darstellen kann. Es ist durchaus spannend, sich die Ergebnisse anzusehen.
Man findet damit relativ schnell heraus, bei welchen Zahlen das Maximum der Möglichkeiten liegt, und wie hoch dieses ist.
Die Zahlen mit einem Minimum an Möglichkeiten muss man nicht berechnen. Denn es handelt sich dabei offensichtlich um die Zahlen 1, 4, 11, 29, 76, 199, 521, 1.364, 3.571, 9.349, 24.476, 10.946, ...
Wie komme ich auf diese Zahlen? Nun, wenn man sie im Φ-Stellenwertsystem aufschreibt, sieht man es sofort – es bedarf keiner weiteren Erklärung:
| 110 | = | 1 | Φ | |
| 410 | = | 101 | , | 01Φ |
| 1110 | = | 10101 | , | 0101Φ |
| 2910 | = | 1010101 | , | 010101Φ |
| 7610 | = | 101010101 | , | 01010101Φ |
| 19910 | = | 10101010101 | , | 0101010101Φ |
| 52110 | = | 1010101010101 | , | 010101010101Φ |
| ⋮ | ⋮ | |||
Nicht ganz so offensichtlich ist die Situation bei den Maxima. Grundsätzlich ist jedoch zu vermuten, dass jeweils zwischen zwei Minimen ein Maximum zu finden ist. Suchen wir ein wenig danach. Zu diesem Zweck liste ich eine Reihe der ersten Dezimalzahlen und ihre entsprechenden »Ideal-Formen« im Φ-System auf, daneben notiere ich die Anzahl der Möglichkeiten, die man innerhalb des Zahlenkörpers hat, um die Zahl zu bilden.
In zwei weiteren Spalten steht jeweils ein »ja«, wenn die Anzahl der Möglichkeiten (Spalte »M«) einem Minimum bzw. einem Maximum entspricht.
Wie ich herausgefunden habe, entspricht ein Maximum an Möglichkeiten jeweils genau dem Wert der Dezimalzahl selbst. Dies ist bei den Zahlen 1, 2, 5, 13, 34, 89, 233, 610, 1.597, 4.181, 10.946, ... der Fall. Aufmerksame Leser erkennen darin jede zweite Fibonacci-Zahl: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1.597, 2.584, 4.181, 6.765, 10.946, ...
Wo M das Minimum von 1 bildet, findet sich jeweils jede zweite Lucas-Zahl: 2, 1, 3, 4, 7, 11, 18, 29, 47, 76, 123, 199, 322, 521, 843, 1.364, 2.207, 3.571, 5.778, 9.349, 15.127, 24.476, ...
| N10 | NΦ | M | Min. | Max. | ||||||
| 1 | 1 | Φ | 1 | ja | ja | |||||
| 2 | 10 | , | 01Φ | 2 | ja | |||||
| 3 | 100 | , | 01Φ | 2 | ||||||
| 4 | 101 | , | 01Φ | 1 | ja | |||||
| 5 | 1000 | , | 1001Φ | 5 | ja | |||||
| 6 | 1010 | , | 0001Φ | 5 | ||||||
| 7 | 10000 | , | 0001Φ | 4 | ||||||
| 8 | 10001 | , | 0001Φ | 5 | ||||||
| 9 | 10010 | , | 0101Φ | 4 | ||||||
| 10 | 10100 | , | 0101Φ | 3 | ||||||
| 11 | 10101 | , | 0101Φ | 1 | ja | |||||
| 12 | 100000 | , | 101001Φ | 10 | ||||||
| 13 | 100010 | , | 001001Φ | 13 | ja | |||||
| 14 | 100100 | , | 001001Φ | 12 | ||||||
| 15 | 100101 | , | 001001Φ | 12 | ||||||
| 16 | 101000 | , | 100001Φ | 13 | ||||||
| 17 | 101010 | , | 000001Φ | 10 | ||||||
| 18 | 1000000 | , | 000001Φ | 6 | ||||||
| 19 | 1000001 | , | 000001Φ | 11 | ||||||
| 20 | 1000010 | , | 010001Φ | 12 | ||||||
| 21 | 1000100 | , | 010001Φ | 13 | ||||||
| 22 | 1000101 | , | 010001Φ | 9 | ||||||
| 23 | 1001000 | , | 100101Φ | 10 | ||||||
| 24 | 1001010 | , | 000101Φ | 10 | ||||||
| 25 | 1010000 | , | 000101Φ | 7 | ||||||
| 26 | 1010001 | , | 000101Φ | 8 | ||||||
| 27 | 1010010 | , | 010101Φ | 6 | ||||||
| 28 | 1010100 | , | 010101Φ | 4 | ||||||
| 29 | 1010101 | , | 010101Φ | 1 | ja | |||||
| 30 | 10000000 | , | 10101001Φ | 17 | ||||||
| 31 | 10000010 | , | 00101001Φ | 25 | ||||||
| 32 | 10000100 | , | 00101001Φ | 27 | ||||||
| 33 | 10000101 | , | 00101001Φ | 27 | ||||||
| 34 | 10001000 | , | 10001001Φ | 34 | ja | |||||
| 35 | 10001010 | , | 00001001Φ | 29 | ||||||
| 36 | 10010000 | , | 00001001Φ | 20 | ||||||
| 37 | 10010001 | , | 00001001Φ | 32 | ||||||
| 38 | 10010010 | , | 01001001Φ | 32 | ||||||
| 39 | 10010100 | , | 01001001Φ | 32 | ||||||
| 40 | 10010101 | , | 01001001Φ | 20 | ||||||
| 41 | 10100000 | , | 10100001Φ | 29 | ||||||
| 42 | 10100010 | , | 00100001Φ | 34 | ||||||
| 43 | 10100100 | , | 00100001Φ | 27 | ||||||
| 44 | 10100101 | , | 00100001Φ | 27 | ||||||
| 45 | 10101000 | , | 10000001Φ | 25 | ||||||
| 46 | 10101010 | , | 00000001Φ | 17 | ||||||
| 47 | 100000000 | , | 00000001Φ | 8 | ||||||
| 48 | 100000001 | , | 00000001Φ | 19 | ||||||
| 49 | 100000010 | , | 01000001Φ | 24 | ||||||
| 50 | 100000100 | , | 01000001Φ | 29 | ||||||
| 51 | 100000101 | , | 01000001Φ | 23 | ||||||
| 52 | 100001000 | , | 10010001Φ | 30 | ||||||
| 53 | 100001010 | , | 00010001Φ | 30 | ||||||
| 54 | 100010000 | , | 00010001Φ | 25 | ||||||
| 55 | 100010001 | , | 00010001Φ | 34 | ||||||
| 56 | 100010010 | , | 01010001Φ | 30 | ||||||
| 57 | 100010100 | , | 01010001Φ | 26 | ||||||
| 58 | 100010101 | , | 01010001Φ | 13 | ||||||
| 59 | 100100000 | , | 10100101Φ | 20 | ||||||
| 60 | 100100010 | , | 00100101Φ | 26 | ||||||
| 61 | 100100100 | , | 00100101Φ | 24 | ||||||
| 62 | 100100101 | , | 00100101Φ | 24 | ||||||
| 63 | 100101000 | , | 10000101Φ | 26 | ||||||
| 64 | 100101010 | , | 00000101Φ | 20 | ||||||
| 65 | 101000000 | , | 00000101Φ | 11 | ||||||
| 66 | 101000001 | , | 00000101Φ | 19 | ||||||
| 67 | 101000010 | , | 01000101Φ | 20 | ||||||
| 68 | 101000100 | , | 01000101Φ | 21 | ||||||
| 69 | 101000101 | , | 01000101Φ | 14 | ||||||
| 70 | 101001000 | , | 10010101Φ | 15 | ||||||
| 71 | 101001010 | , | 00010101Φ | 15 | ||||||
| 72 | 101010000 | , | 00010101Φ | 10 | ||||||
| 73 | 101010001 | , | 00010101Φ | 11 | ||||||
| 74 | 101010010 | , | 01010101Φ | 8 | ||||||
| 75 | 101010100 | , | 01010101Φ | 5 | ||||||
| 76 | 101010101 | , | 01010101Φ | 1 | ja | |||||
| 77 | 1000000000 | , | 1010101001Φ | 26 | ||||||
| 78 | 1000000010 | , | 0010101001Φ | 41 | ||||||
| 79 | 1000000100 | , | 0010101001Φ | 48 | ||||||
| 80 | 1000000101 | , | 0010101001Φ | 48 | ||||||
| 81 | 1000001000 | , | 1000101001Φ | 65 | ||||||
| 82 | 1000001010 | , | 0000101001Φ | 58 | ||||||
| 83 | 1000010000 | , | 0000101001Φ | 45 | ||||||
| 84 | 1000010001 | , | 0000101001Φ | 72 | ||||||
| 85 | 1000010010 | , | 0100101001Φ | 72 | ||||||
| 86 | 1000010100 | , | 0100101001Φ | 72 | ||||||
| 87 | 1000010101 | , | 0100101001Φ | 45 | ||||||
| 88 | 1000100000 | , | 1010001001Φ | 73 | ||||||
| 89 | 1000100010 | , | 0010001001Φ | 89 | ja | |||||
| 90 | 1000100100 | , | 0010001001Φ | 75 | ||||||
| 91 | 1000100101 | , | 0010001001Φ | 75 | ||||||
| 92 | 1000101000 | , | 1000001001Φ | 74 | ||||||
Was ist nun die Voraussetzung, um das Maximum an Möglichkeiten auszuschöpfen? Es ist eine bestimmte Anordnung der Potenzen. Sehen wir uns die Zahlen an, bei denen es ein Maximum an Möglichkeiten gibt, dann ist es wie bei den Minimen: Das Muster springt sofort ins Auge und erklärt sich fast von selbst.
| 1 | 1 | |||
| 2 | 10 | , | 01 | |
| 5 | 1000 | , | 1001 | |
| 13 | 100010 | , | 001001 | |
| 34 | 10001000 | , | 10001001 | |
| 89 | 1000100010 | , | 0010001001 | |
| 233 | 100010001000 | , | 100010001001 | |
| 610 | 10001000100010 | , | 00100010001001 | |
| 1.597 | 1000100010001000 | , | 1000100010001001 | |
| ⋮ | ⋮ | |||
Lässt man die Zahlen 1 und 2 beiseite (diese unterliegen noch einer gewissen »Unschärfe«), so sieht man, dass die Zahlen jeweils eine Folge von 1000-1000-... bilden. Ein »Zwischenraum« von genau 3 Nullen zwischen einer 1 ist das Optimum, damit möglichst viele Kombinationen entstehen können. Wird der Zwischenraum größer (4 oder mehr Nullen), dann haben dort weniger Möglichkeiten Platz! Man kann das leicht an einer Zahl sehen, die sehr viele Nullen zwischen zwei Einsern hat – beispielsweise die Zahl 123. Im Φ-System geschrieben sieht das so aus:
123 10000000000,0000000001
Es gibt lediglich 10 Möglichkeiten innerhalb des Zahlenkörpers der Zahl 123, sie im Φ-System aufzuschreiben:
| 10000000000,0000000001 |
| 1100000000,0000000001 |
| 1011000000,0000000001 |
| 1010110000,0000000001 |
| 1010101100,0000000001 |
| 1010101011,0000000001 |
| 1010101010,1100000001 |
| 1010101010,1011000001 |
| 1010101010,1010110001 |
| 1010101010,1010101101 |
Füge ich in der Mitte (links vom Komma) eine 1 hinzu (das ergibt die Dezimalzahl 124), so erhöht sich die Anzahl der Möglichkeiten sprungartig von 10 auf 29:
| 10000000001,0000000001 |
| 10000000000,1100000001 |
| 10000000000,1011000001 |
| 10000000000,1010110001 |
| 10000000000,1010101101 |
| 1100000001,0000000001 |
| 1100000000,1100000001 |
| 1100000000,1011000001 |
| 1100000000,1010110001 |
| 1100000000,1010101101 |
| 1011000001,0000000001 |
| 1011000000,1100000001 |
| 1011000000,1011000001 |
| 1011000000,1010110001 |
| 1011000000,1010101101 |
| 1010110001,0000000001 |
| 1010110000,1100000001 |
| 1010110000,1011000001 |
| 1010110000,1010110001 |
| 1010110000,1010101101 |
| 1010101101,0000000001 |
| 1010101100,1100000001 |
| 1010101100,1011000001 |
| 1010101100,1010110001 |
| 1010101100,1010101101 |
| 1010101011,1100000001 |
| 1010101011,1011000001 |
| 1010101011,1010110001 |
| 1010101011,1010101101 |
Eine Kleinigkeit wäre noch zu erwähnen: Die Zahlen mit maximalen Möglichkeiten enden auf der »rechten« Seite nicht mit ...10001 sondern mit ...1001. Das hat einen bestimmten Grund. Das rechte Ende der »Hülle« im Zahlenkörper bildet den Übergang zu den unendlich vielen Möglichkeiten »außerhalb« davon. Man kann die »Hülle« anstatt mit ...1001 auch mit ...100011 abschließen, dann hat man wieder die »optimalen« 3 Nullen dazwischen.
Zum Abschluss für heute verweise ich nochmal auf den Möglichkeiten-Rechner, mit dem man alles spielerisch ausprobieren kann.
| 1 | Benannt nach Francis Galton (1822 – 1911), britischer Naturforscher und Schriftsteller |
| 2 | Nach Carl Friedrich Gauß (1777 – 1855), deutscher Mathematiker, Astronom, Physiker, Geodät |
Diese Seite herunterladen: PDF ODT
 |
 |
|