 |
Inhalt • Suchen | |
2020-12-20
Dreiecke
Im letzten Text vom 29.11.2020 konnte man sehen, dass man jeden Wert im Pascalschen Dreieck nicht nur durch fortgesetztes Addieren, sondern auch durch fortgesetztes Multiplizieren innerhalb der jeweiligen Zeile erhalten kann. Da das Dreieck symmetrisch ist, funktioniert die Multiplikations-Kette von beiden Seiten der Zeile aus.
Ich muss lediglich die Zeilennummer wissen, um die vollständige Kette berechnen zu können – mehr ist nicht nötig. Im Beispiel des letzten Artikels war dies die Zeile Nr. 8. Die Zeilennummer kann auf beiden Seiten stets in der zweiten Wabe von außen abgelesen werden.
Heute verwende ich ein etwas größeres Dreieck und mache das Gleiche mit der Zeile Nr. 13, in welcher sich u. a. der Wert 715 befindet:
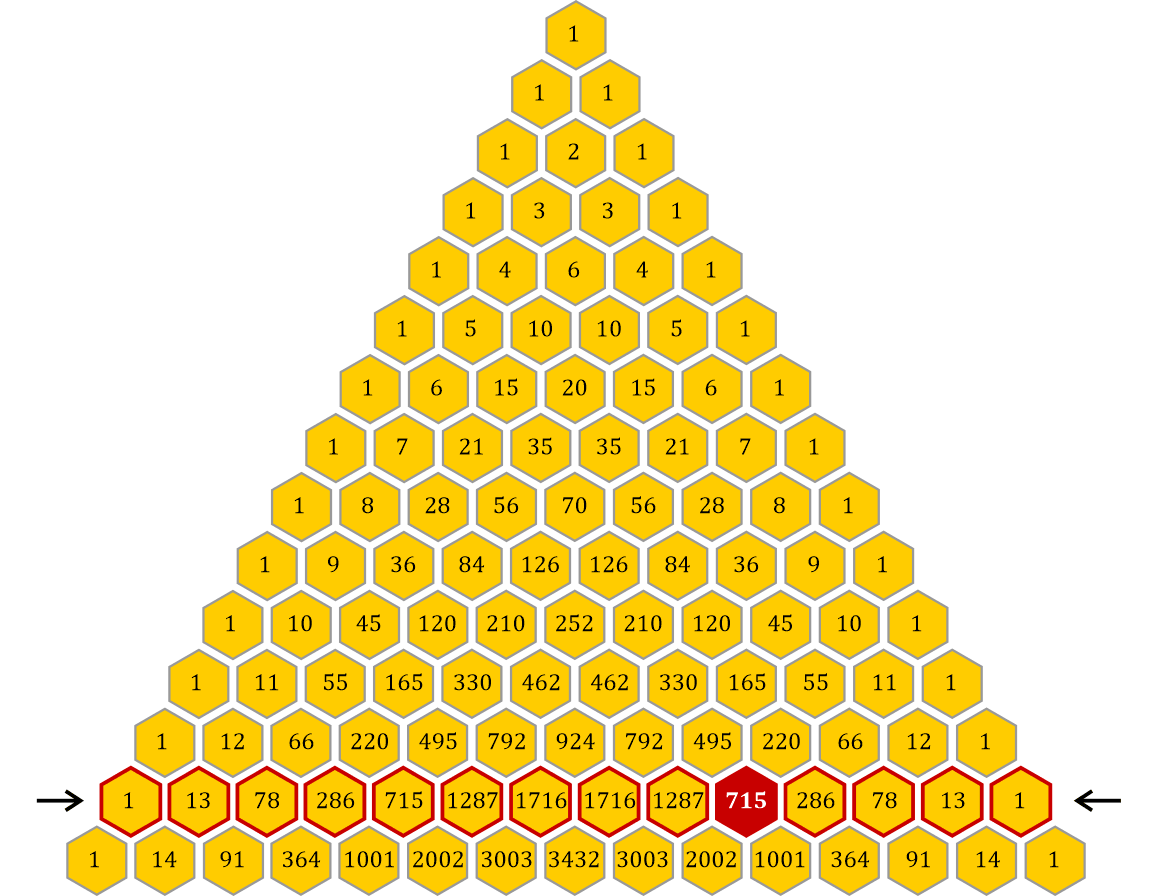
Ich beginne die Multiplikation in der Zeile mit der Zeilennummer 13 und arbeite mich dann über die einzelnen Waben voran:
Die erste Wabe mit der Zeilennummer 13 wird durch die Wabennummer 1 dividiert:
|
Der äußerste Rand, der aus lauter 1ern besteht, wird nicht mitgezählt – er ist das »Verbindungsglied« des Möbius-Bandes. Um den Wert der Wabe Nr. 2 zu erhalten, reduziere ich den Nenner in der Multiplikationskette um 1 und erhöhe den Zähler um 1:
|
Ich erhalte für die Wabe Nr. 2 somit den Wert
| 13 |
| 1 |
| 12 |
| 2 |
Wabe Nr. 3 enthält den Wert
| 13 |
| 1 |
| 12 |
| 2 |
| 11 |
| 3 |
und so weiter. Die vollständige Multiplikationskette bis zur Wabe mit dem Wert 715 sieht, wenn man von links beginnt, so aus:
| 13 |
| 1 |
| 12 |
| 2 |
| 11 |
| 3 |
| 10 |
| 4 |
| 9 |
| 5 |
| 8 |
| 6 |
| 7 |
| 7 |
| 6 |
| 8 |
| 5 |
| 9 |
Beginnt man von der rechten Seite aus, so ist der Weg kürzer:
| 13 |
| 1 |
| 12 |
| 2 |
| 11 |
| 3 |
| 10 |
| 4 |
Ich habe mich nun gefragt, ob eine solche Multiplikationskette auch von einer anderen Seite aus funktioniert. Die einzelnen Waben des Dreiecks sind 6-eckig und somit gibt es noch zwei weitere Richtungen, in denen man multiplizieren könnte:
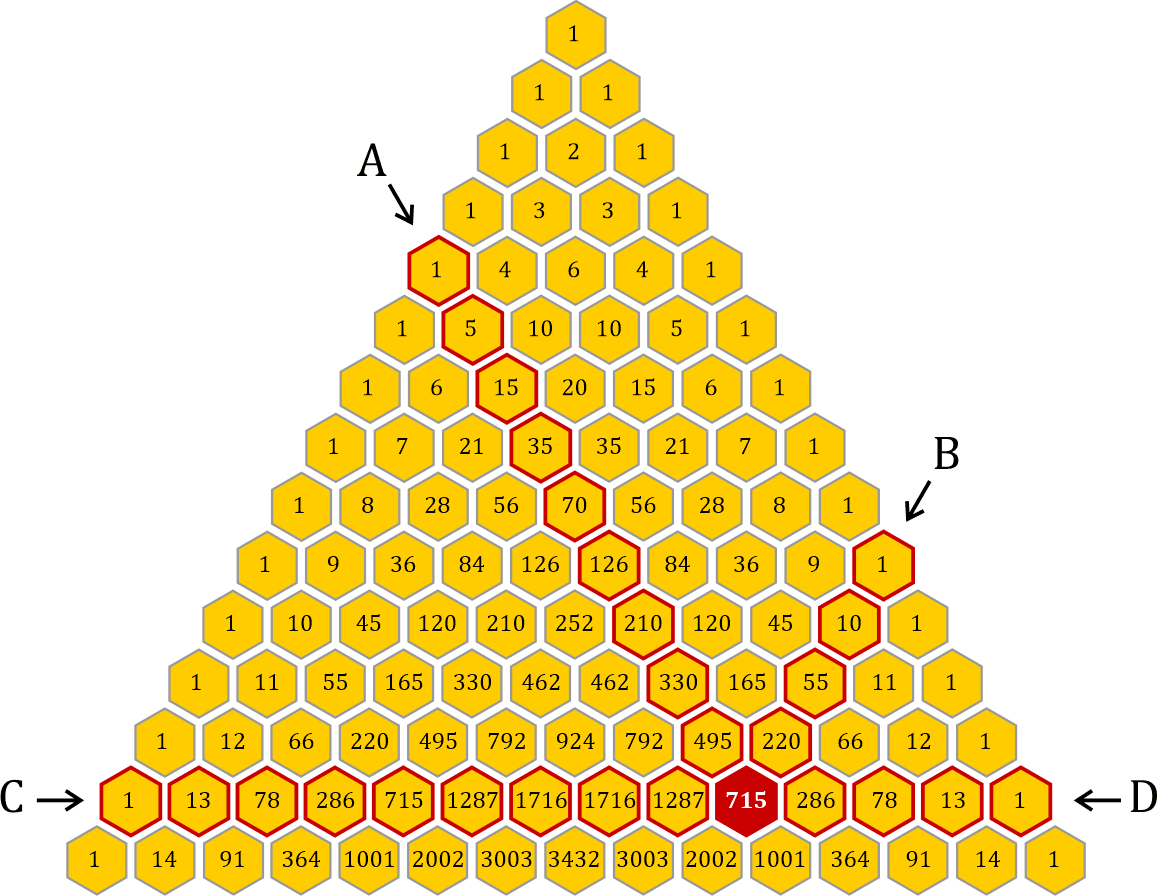
Die beiden »unteren« Seiten scheiden als Möglichkeit aus, da das Dreieck auf dieser Seite »offen« ist – hier laufen die Zahlen in alle Ewigkeit weiter. Aber die beiden um jeweils 60° gedrehten Ketten von oben funktionieren genauso wie die horizontalen. Ich beginne wieder mit der ersten Wabe innerhalb des Randes, das ist im Fall von links oben die Wabe mit der Zeilennummer 5,
|
und errechne den Wert der nächsten Wabe, indem ich mit
|
multipliziere:
| 5 |
| 1 |
| 6 |
| 2 |
Der einzige Unterschied in der Vorgangsweise zur horizontalen Kette besteht darin, dass ich den Zähler der einzelnen Glieder nicht um 1 verringere, sondern so wie den Nenner ebenfalls um 1 erhöhe.
Ich setze die Kette fort und erhalte den Wert der nächsten Wabe mit
| 5 |
| 1 |
| 6 |
| 2 |
| 7 |
| 3 |
Die vollständige Kette von links oben sieht wie folgt aus:
| 5 |
| 1 |
| 6 |
| 2 |
| 7 |
| 3 |
| 8 |
| 4 |
| 9 |
| 5 |
| 10 |
| 6 |
| 11 |
| 7 |
| 12 |
| 8 |
| 13 |
| 9 |
Rechne es bitte nach, du erhältst mit jeder Multiplikation immer den Wert der nächsten Wabe.
Der kürzere Weg zur Wabe mit dem Wert 715 ist jener von rechts oben, denn er beginnt bereits mit dem Wert
|
und enthält nur 4 Glieder:
| 10 |
| 1 |
| 11 |
| 2 |
| 12 |
| 3 |
| 13 |
| 4 |
Auch diese Kette ergibt auf jeder »Station« jeweils genau den entsprechenden Wabenwert, wie man leicht nachrechnen kann.
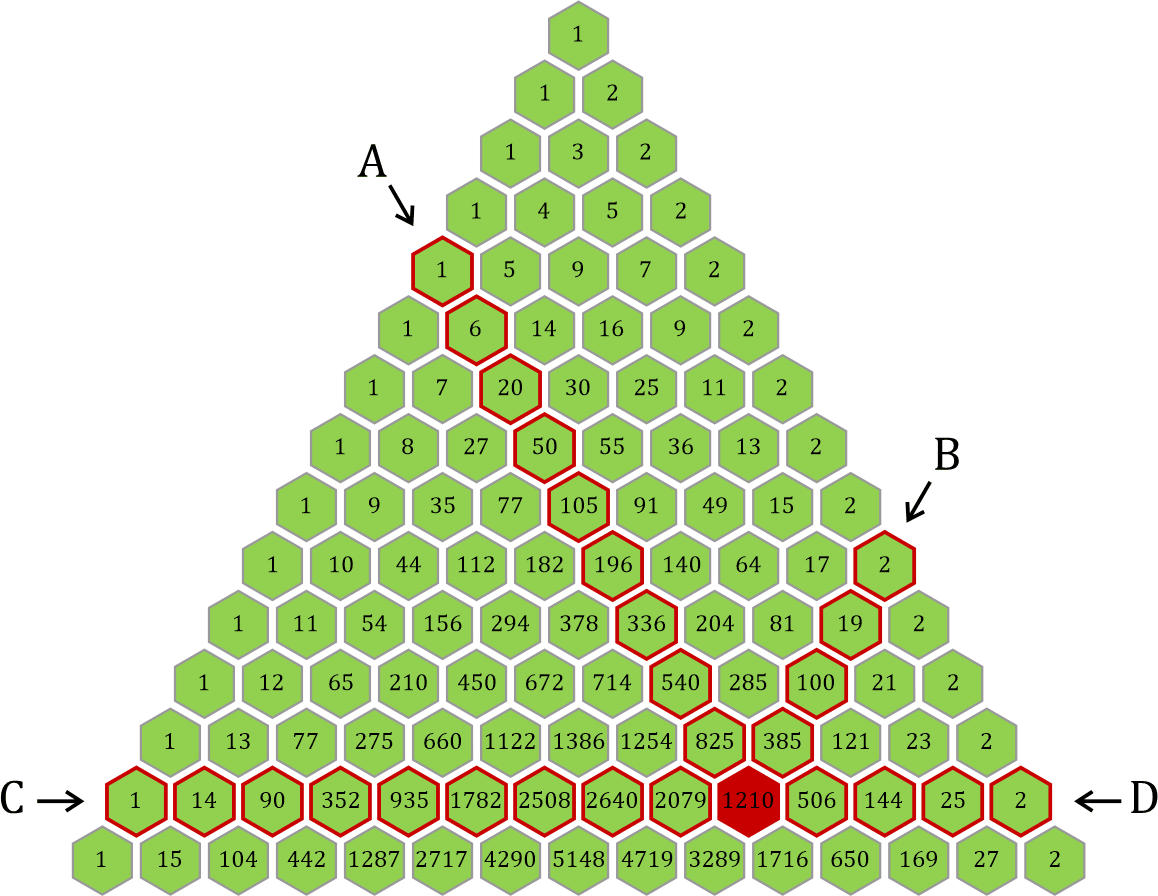
Wie sieht dieses »Ketten-Verhalten« nun bei unserem anderen Dreieck aus, dem Phi-Dreieck? Kann ich hier auch solche Multiplikationsketten bilden? Die Antwort ist: Im Prinzip ja, aber da dieses Dreieck eine multidimensionale Struktur hat, wie wir andeutungsweise schon gesehen haben, sind diese Ketten alles andere als »linear«:
| 2 ⋅ 3 |
| 1 |
| 2 ⋅ 5 |
| 3 |
| 5 |
| 2 |
| 3 ⋅ 7 |
| 2 ⋅ 5 |
| 2 ⋅ 2 ⋅ 7 |
| 3 ⋅ 5 |
| 2 ⋅ 2 ⋅ 3 |
| 7 |
| 3 ⋅ 3 ⋅ 5 |
| 2 ⋅ 2 ⋅ 7 |
| 5 ⋅ 11 |
| 2 ⋅ 2 ⋅ 3 ⋅ 3 |
| 2 ⋅ 11 |
| 3 ⋅ 5 |
| 2 |
| 1 |
| 19 |
| 2 |
| 2 ⋅ 2 ⋅ 5 ⋅ 5 |
| 19 |
| 7 ⋅ 11 |
| 2 ⋅ 2 ⋅ 5 |
| 2 ⋅ 11 |
| 7 |
| 2 ⋅ 7 |
| 1 |
| 3 ⋅ 3 ⋅ 5 |
| 7 |
| 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 11 |
| 3 ⋅ 3 ⋅ 5 |
| 5 ⋅ 17 |
| 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 |
| 2 ⋅ 3 ⋅ 3 ⋅ 3 ⋅ 3 |
| 5 ⋅ 17 |
| 2 ⋅ 19 |
| 3 ⋅ 3 ⋅ 3 |
| 2 ⋅ 2 ⋅ 5 |
| 19 |
| 3 ⋅ 3 ⋅ 7 |
| 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 5 |
| 2 ⋅ 5 ⋅ 11 |
| 3 ⋅ 3 ⋅ 3 ⋅ 7 |
| 2 |
| 1 |
| 5 ⋅ 5 |
| 2 |
| 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 3 ⋅ 3 |
| 5 ⋅ 5 |
| 11 ⋅ 23 |
| 2 ⋅ 2 ⋅ 2 ⋅ 3 ⋅ 3 |
| 5 ⋅ 11 |
| 23 |
Immerhin: Es gibt eine sehr wichtige Gemeinsamkeit mit dem »linearen« Pascalschen Dreieck. Alle Primzahlen des Dreiecks liegen ausschließlich auf den äußeren beiden »zweiten Streifen«:1)
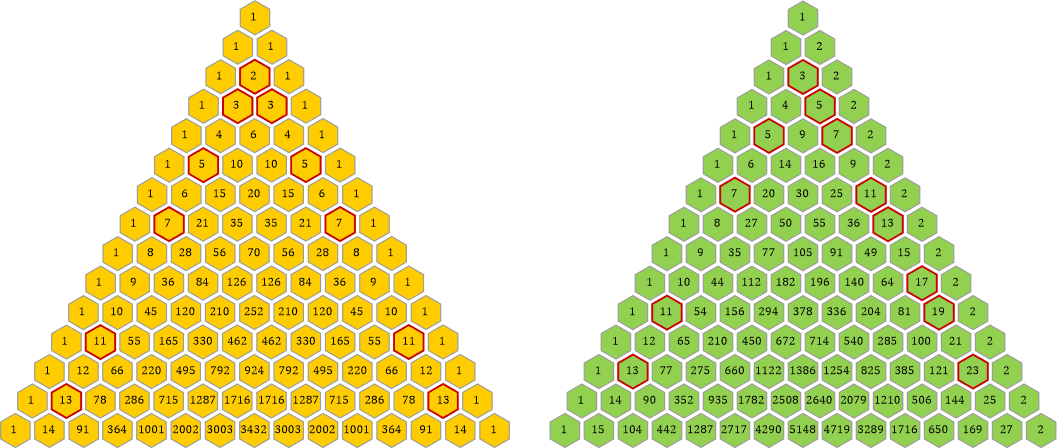
Dies ist durch die Multiplikationsketten auch sofort mathematisch bewiesen, denn sobald ich eine Zahl mit einer anderen multipliziere, kann das Ergebnis keine Primzahl mehr sein.
Das Wort Primzahl leitet sich vom lateinischen numerus primus ab – das bedeutet »erste Zahl«. Diese »ersten Zahlen« sind im Pascalschen Dreieck so exakt geordnet wie sonst nirgendwo. Im Grunde ist das Pascalsche Dreieck nichts anderes als eine wohlgeordnete Überlagerung lauter Dreiecke, die aus nichts als diesen Primzahlen bestehen. Das Pascalsche Dreieck besteht aus lauter »Schichten von Primdreiecken«, wie wir gleich sehen werden. Ein Primdreieck ist ein Dreieck aus lauter Primzahlen, dessen Seitenlänge um 1 kleiner ist als die Primzahlen, aus denen es zusammengesetzt ist.
Primzahlen sind dadurch definiert: Sie sind ganze Zahlen (»Natürliche Zahlen«), die nur durch sich selbst und durch 1 ganzzahlig teilbar sind. Die Zahl 1 erfüllt diese Anforderung ebenfalls, wird von den Mathematikern allerdings aus einem mir nicht nachvollziehbaren Grund nicht zu den Primzahlen gezählt – obwohl sie doch die »erste unter den ersten Zahlen« ist ...
Diese »ersten Zahlen« sind den meisten Menschen bekannt. Die Primzahlen innerhalb des Bereichs von 2 bis 100 lauten:
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97.
Darüber hinaus gibt es noch unendlich viele weitere Primzahlen – sie hören nie auf, werden allerdings mit zunehmender Größe immer seltener.
Fragt man jemanden, wie die Primfaktoren im Pascalschen Dreieck angeordnet sind, so kann es sein, dass man die Antwort erhält: Wie im Sierpinski-Dreieck! Wir werden gleich sehen, dass dies richtig ist.
Nehmen wir als erstes Beispiel die Primzahl 3 und schauen uns an, welche Zahlen im Pascalschen Dreieck durch 3 teilbar sind. Ich habe sie mit einem blauen Hintergrund versehen:
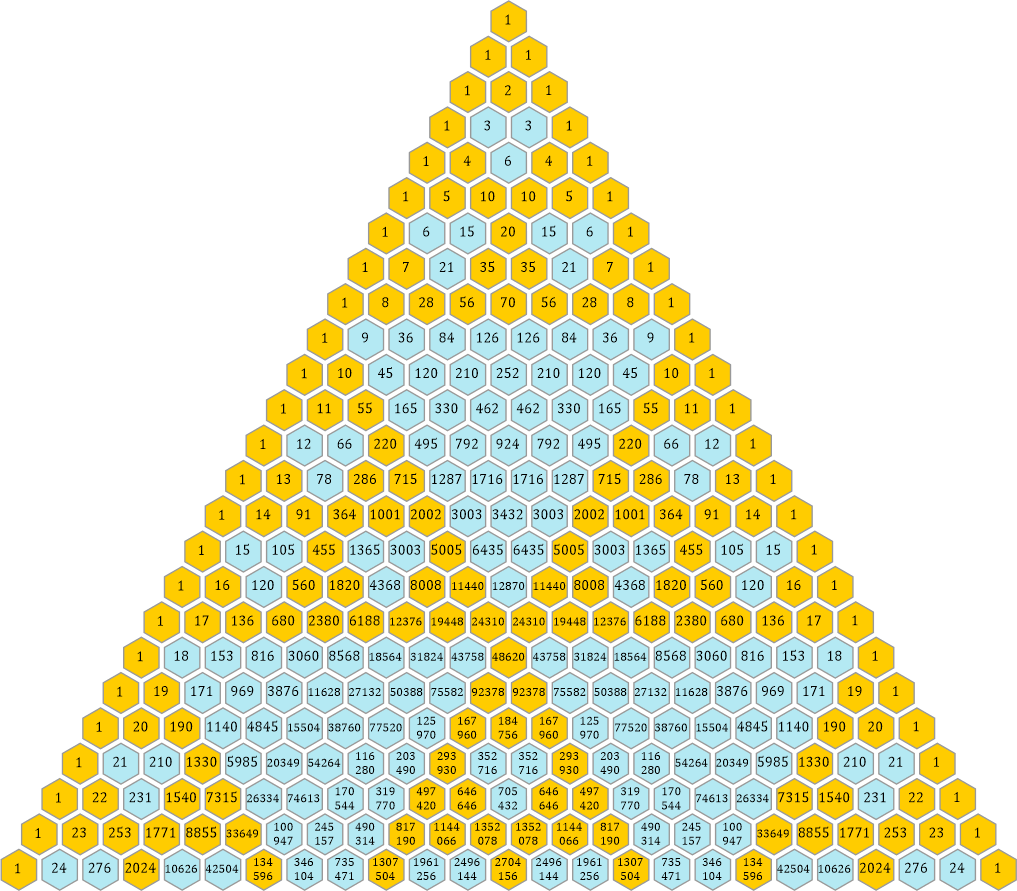
Schön regelmäßig! Und nach genau diesem Muster sind alle Zahlen im Pascalschen Dreieck angeordnet. Die kleinste (»offizielle«) Primzahl ist 2, das Muster dieses Dreiecks sieht so aus:
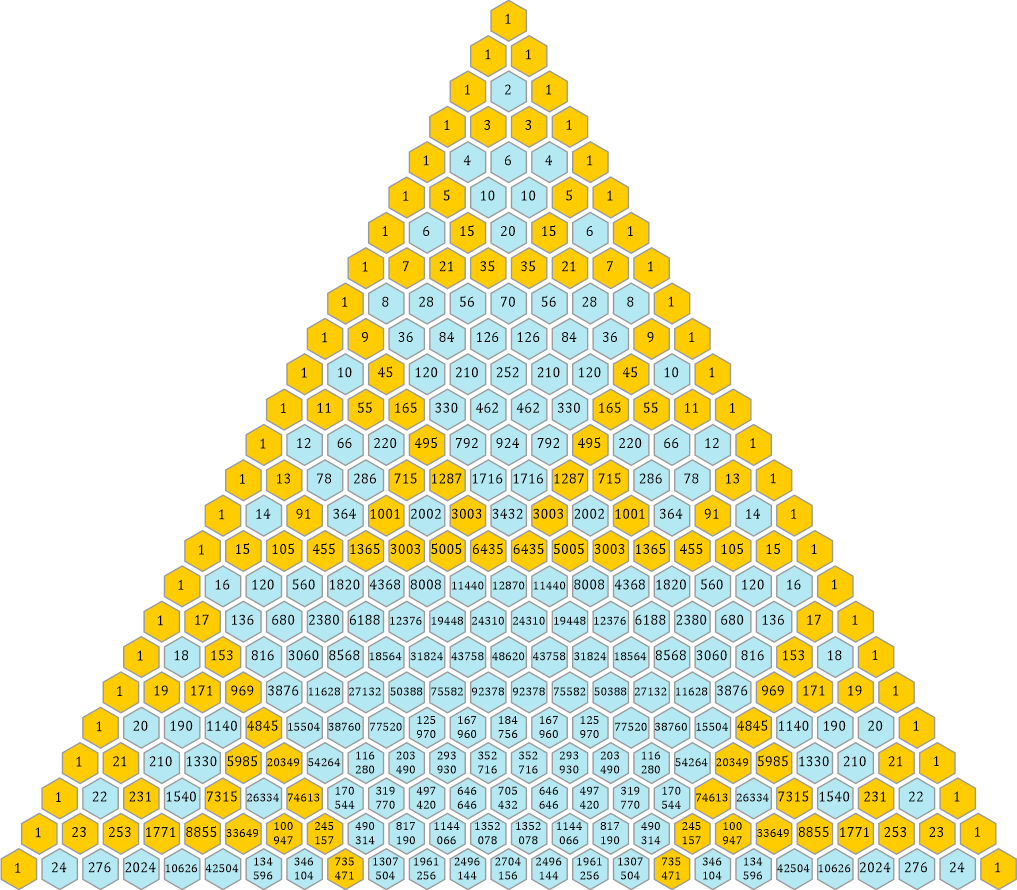
Jedes der Dreiecke hält stets einen Mindestabstand von genau einer Wabe zum nächsten Dreieck ein. Das kleinstmögliche Dreieck hat eine Seitenlänge von p − 1, wobei p die gewählte Primzahl ist. In diesem Fall ist p = 2, daher hat das kleinste Dreieck eine Seitenlänge s von nur 1. Die Größe der Dreiecke wächst mit deren Potenz.
22 = 4, somit hat das nächstgrößere Dreieck eine Seitenlänge von s = 4 − 1 = 3.
Die dritte Größe ist 23 = 8, das ergibt eine Seitenlänge von s = 8 − 1 = 7.
Der weitere Verlauf nach unten ist somit klar:
s = 24 − 1 = 15
s = 25 − 1 = 31
⋮
Hier noch weitere Bilder von Zahlen, die im Pascalschen Dreieck enthalten sind – die blauen Dreiecke enthalten Zahlen, die alle durch 5 teilbar sind:
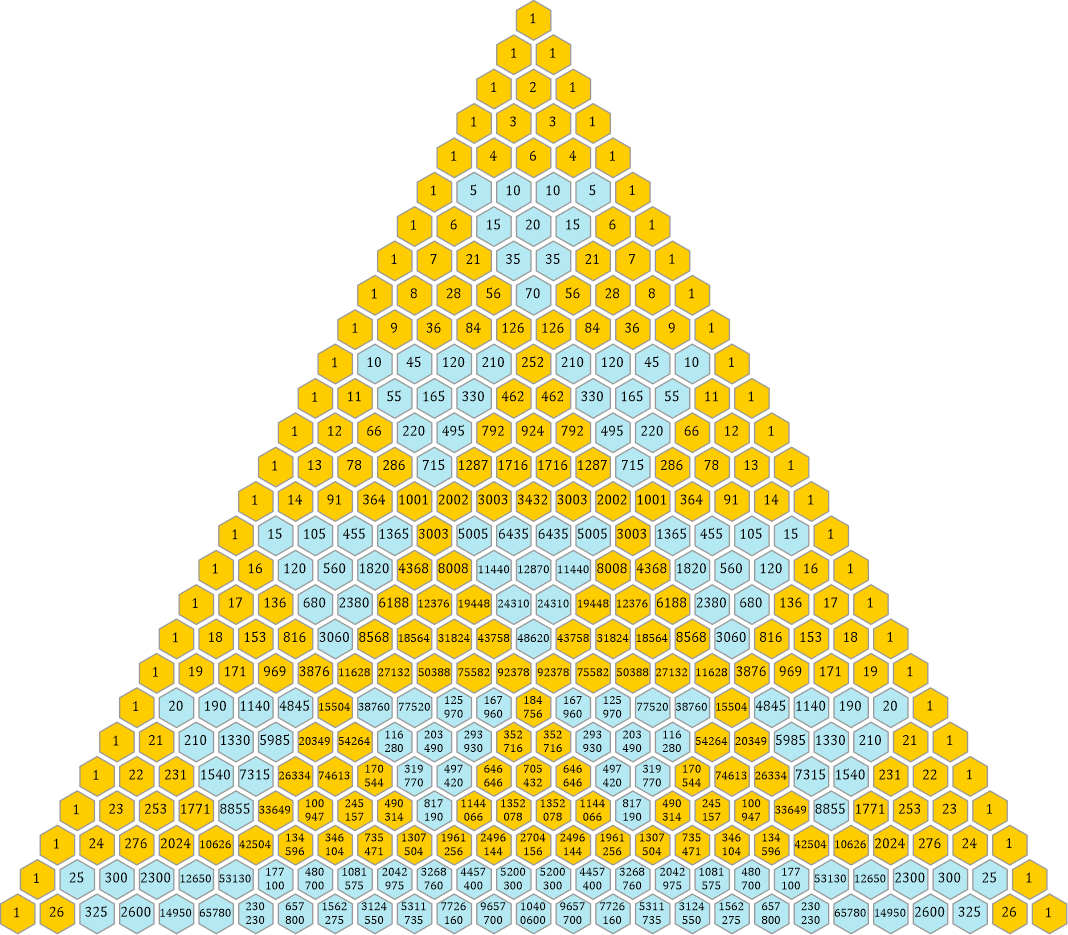
Ich habe das Dreieck im Vergleich zum vorhergehenden am unteren Rand um zwei Zeilen erweitert, dadurch kann man sehen, dass ab der Zeile 25 (das ist 52) ein großes Dreieck beginnt.
Es folgen noch die Dreiecke mit den Zahlen, die durch 7 und 11 teilbar sind:
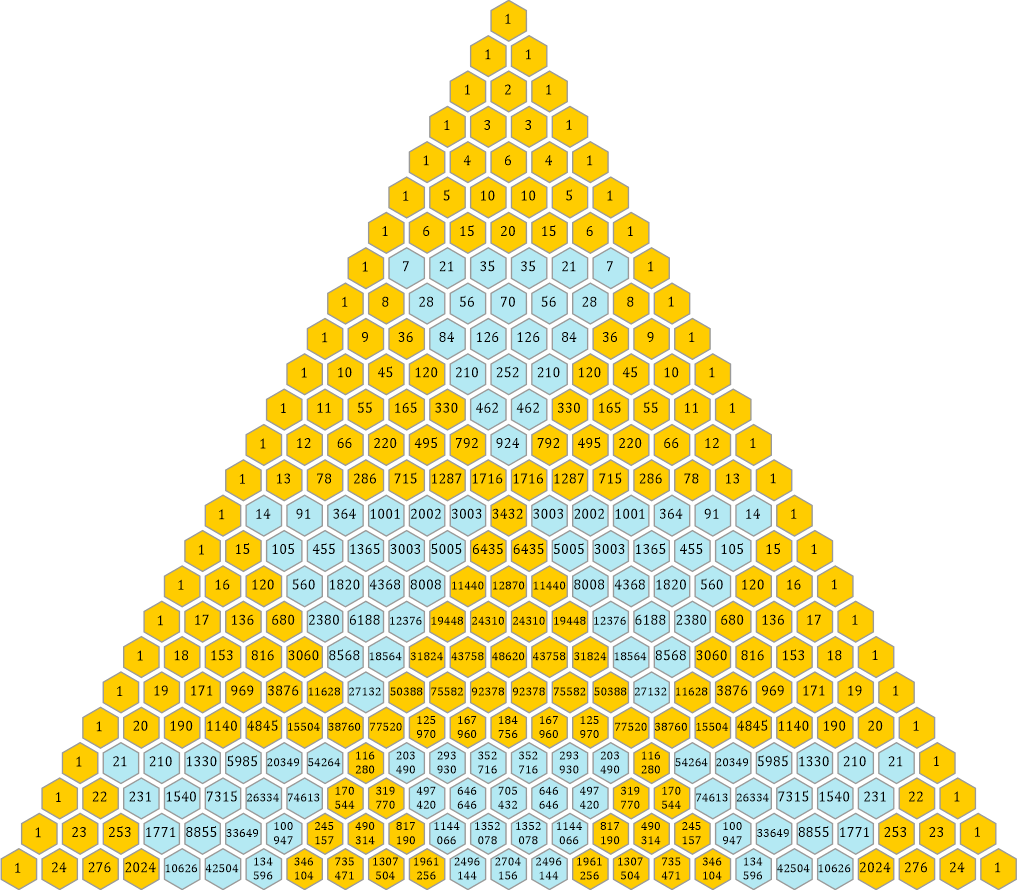

Wie sieht das nun im Fall unseres Phi-Dreiecks aus? Dieses ist ja nichts anderes als das Ergebnis von zwei (minimal verschobenen) überlagerten Pascalschen Dreiecken. Die Ergebnisse sind durchaus ähnlich. Die »großen« Dreiecke haben eine Seitenlänge von n − 2 (statt n − 1) und dazwischen gibt es noch ein paar »Streifen«, die durch die minimale Verschiebung entstehen und sichtbar werden. Aber ansonsten sind die Unterschiede gering.
Beim Pascalschen Dreieck sind die einzelnen Zahlen ausschließlich aus Primzahlen zusammengesetzt, die nicht größer sein können als die Zeilennummer, auf der die Zahl angeordnet ist. Nehmen wir als Beispiel die Zeile Nr. 19

und zerlegen deren Zahlen (ohne die äußere 1) in ihre Primfaktoren:
| 19 | = | 19 |
| 171 | = | 3 ⋅ 3 ⋅ 19 |
| 969 | = | 3 ⋅ 17 ⋅ 19 |
| 3876 | = | 2 ⋅ 2 ⋅ 3 ⋅ 17 ⋅ 19 |
| 11628 | = | 2 ⋅ 2 ⋅ 3 ⋅ 3 ⋅ 17 ⋅ 19 |
| 27132 | = | 2 ⋅ 2 ⋅ 3 ⋅ 7 ⋅ 17 ⋅ 19 |
| 50388 | = | 2 ⋅ 2 ⋅ 3 ⋅ 13 ⋅ 17 ⋅ 19 |
| 75582 | = | 2 ⋅ 3 ⋅ 3 ⋅ 13 ⋅ 17 ⋅ 19 |
| 92378 | = | 2 ⋅ 11 ⋅ 13 ⋅ 17 ⋅ 19 |
Es ist intuitiv verständlich, dass das so sein muss, wenn man über die Multiplikationsketten Bescheid weiß.
Beim Phi-Dreieck können die Primfaktoren doppelt so groß werden wie die Zeilennummer, in welcher die betreffende Zahl angeordnet ist. Der Grund dafür leuchtet ebenfalls schnell ein: Auf der linken Seite ist die Linie, welche die Primzahlen enthält, identisch mit dem Pascalschen Dreieck (sie besteht aus allen Natürlichen Zahlen), auf der rechten Seite kommen jedoch nur alle ungeraden Zahlen vor, daher wachsen dort die Primzahlen doppelt so schnell. Schauen wir uns wiederum die Zeile Nr. 19 an:

Zunächst sei angemerkt, dass im Phi-Dreieck die Linie mit den Natürlichen Zahlen um eine Position nach oben verschoben ist im Vergleich zum Pascalschen Dreieck, daher haben wir in der Zeile 19 in der zweiten Wabe von links die Zahl 20 stehen und nicht die Zahl 19.
Und da das Phi-Dreieck im Gegensatz zum Pascalschen Dreieck nicht symmetrisch ist, enthält es doppelt so viele unterschiedliche Zahlen.
Die Zerlegung der Zahlen in ihre Primfaktoren bringt folgendes Ergebnis:
| 20 | = | 2 ⋅ 2 ⋅ 5 |
| 189 | = | 3 ⋅ 3 ⋅ 3 ⋅ 7 |
| 1122 | = | 2 ⋅ 3 ⋅ 11 ⋅ 17 |
| 4692 | = | 2 ⋅ 2 ⋅ 3 ⋅ 17 ⋅ 23 |
| 14688 | = | 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 3 ⋅ 3 ⋅ 3 ⋅ 17 |
| 35700 | = | 2 ⋅ 2 ⋅ 3 ⋅ 5 ⋅ 5 ⋅ 7 ⋅ 17 |
| 68952 | = | 2 ⋅ 2 ⋅ 2 ⋅ 3 ⋅ 13 ⋅ 13 ⋅ 17 |
| 107406 | = | 2 ⋅ 3 ⋅ 3 ⋅ 3 ⋅ 3 ⋅ 3 ⋅ 13 ⋅ 17 |
| 136136 | = | 2 ⋅ 2 ⋅ 2 ⋅ 7 ⋅ 11 ⋅ 13 ⋅ 17 |
| 140998 | = | 2 ⋅ 11 ⋅ 13 ⋅ 17 ⋅ 29 |
| 119340 | = | 2 ⋅ 2 ⋅ 3 ⋅ 3 ⋅ 3 ⋅ 5 ⋅ 13 ⋅ 17 |
| 82212 | = | 2 ⋅ 2 ⋅ 3 ⋅ 13 ⋅ 17 ⋅ 31 |
| 45696 | = | 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 3 ⋅ 7 ⋅ 17 |
| 20196 | = | 2 ⋅ 2 ⋅ 3 ⋅ 3 ⋅ 3 ⋅ 11 ⋅ 17 |
| 6936 | = | 2 ⋅ 2 ⋅ 2 ⋅ 3 ⋅ 17 ⋅ 17 |
| 1785 | = | 3 ⋅ 5 ⋅ 7 ⋅ 17 |
| 324 | = | 2 ⋅ 2 ⋅ 3 ⋅ 3 ⋅ 3 ⋅ 3 |
| 37 | = | 37 |
Betrachten wir noch die Muster im Phi-Dreieck. Mit Hilfe einer bildlichen Darstellung sind die Unterschiede zum Pascalschen Dreieck viel schneller zu sehen.
Beim Dreieck mit den durch 2 teilbaren Zahlen gibt es am rechten Rand einen durchgehenden Streifen in Blau, da dort lauter 2er stehen:
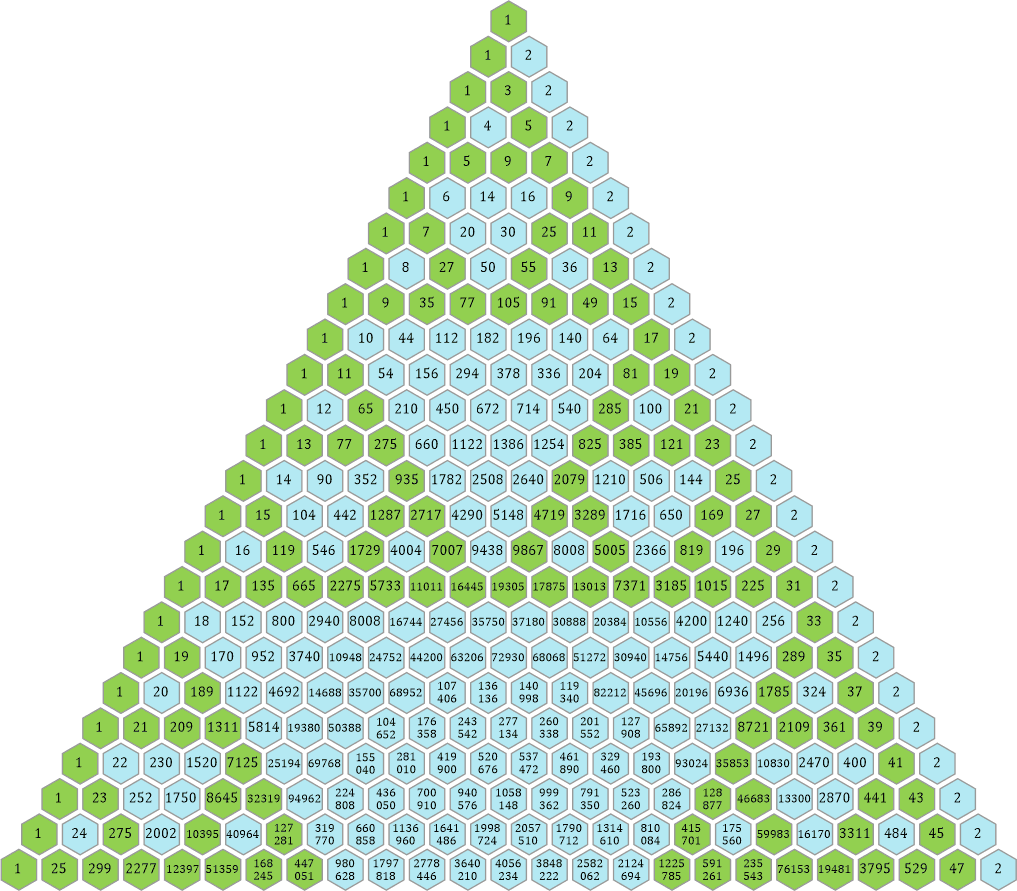
Die einzelnen blauen Waben sind die Reste von zwei überlagerten Dreiecken der Potenz 2, die also im Pascalschen Dreieck eine Seitenlänge von s = 22 − 1 = 3 hatten und jetzt nur noch eine Seitenlänge von s = n − 2 = 3 − 2 = 1 haben. Es gibt somit auch kein einziges kleinstes Dreieck zu sehen, da die Zahl n = 2 ist und die Seitenlänge damit »verschwindet«: s = n − 2 = 0. Als eine Art Ersatz dafür ist der komplette rechte Rand des Phi-Dreiecks mit lauter Waben bestückt, die genau die Zahl 2 enthalten.
Im Dreieck mit den durch 3 teilbaren Zahlen schrumpfen die kleinsten Dreiecke nach der Regel s = n − 2 auf einzelne Waben zusammen. Diese halten wie immer auch die »Abstandsregel« ein: Kein Dreieck darf ein anderes berühren, es muss der Mindestabstand von einer Wabe gewahrt bleiben.
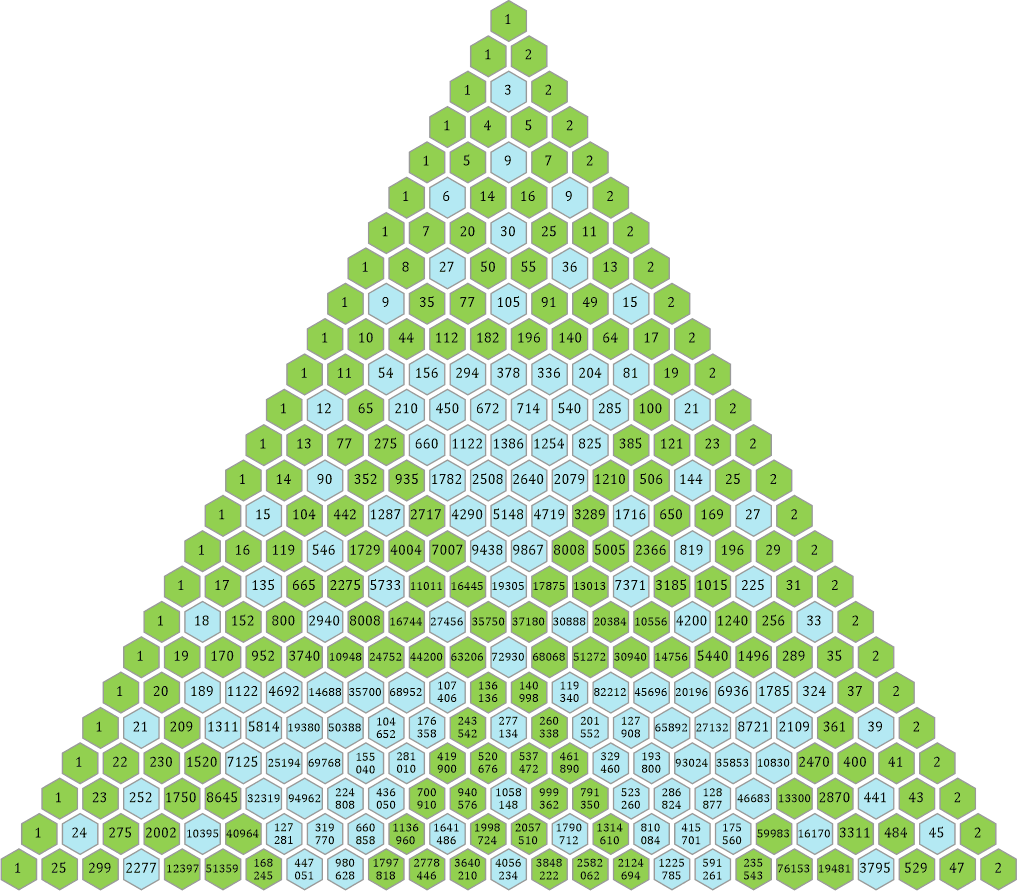
Beim 5er-Dreieck sieht man ganz unten den oberen Rand des ersten »großen« Dreiecks mit s = 52 − 2:
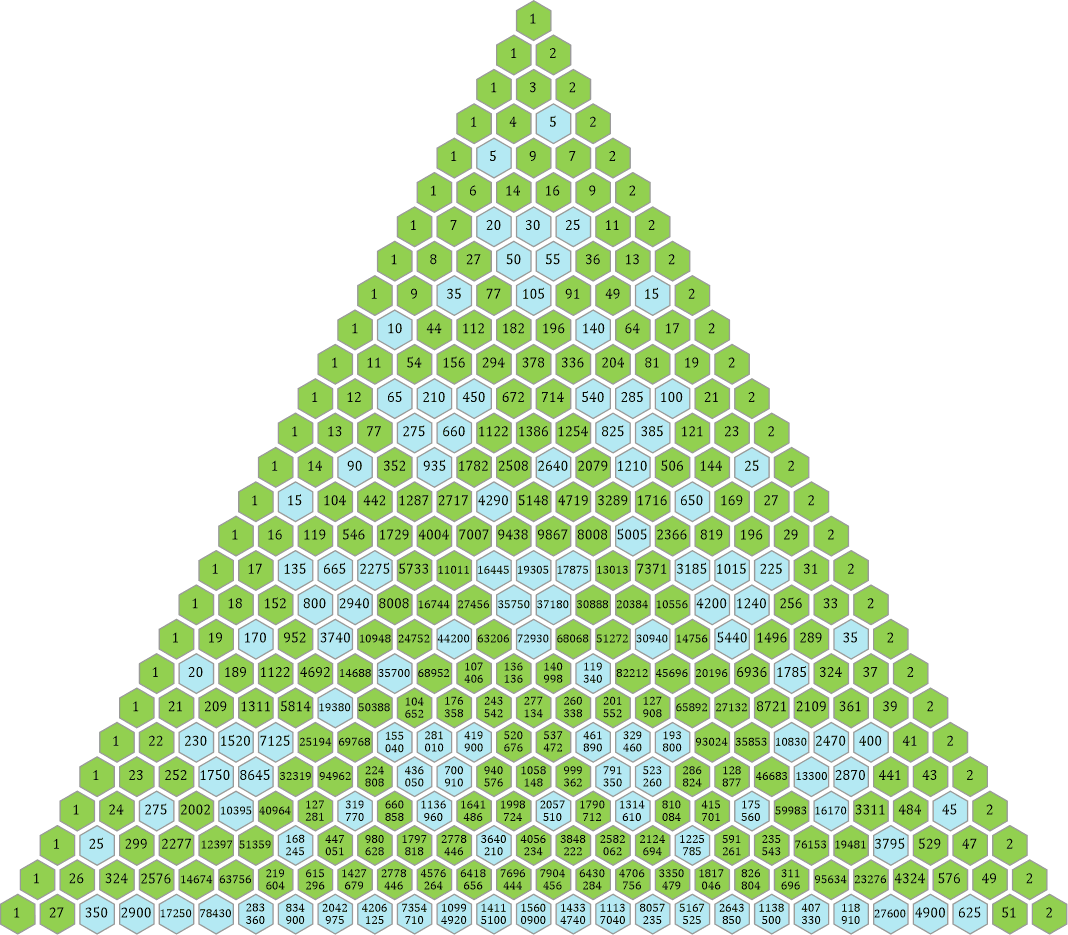
Im 7er-Dreieck sind die »Streifen«, die durch die Verschiebung entstanden sind, schon gut zu sehen.
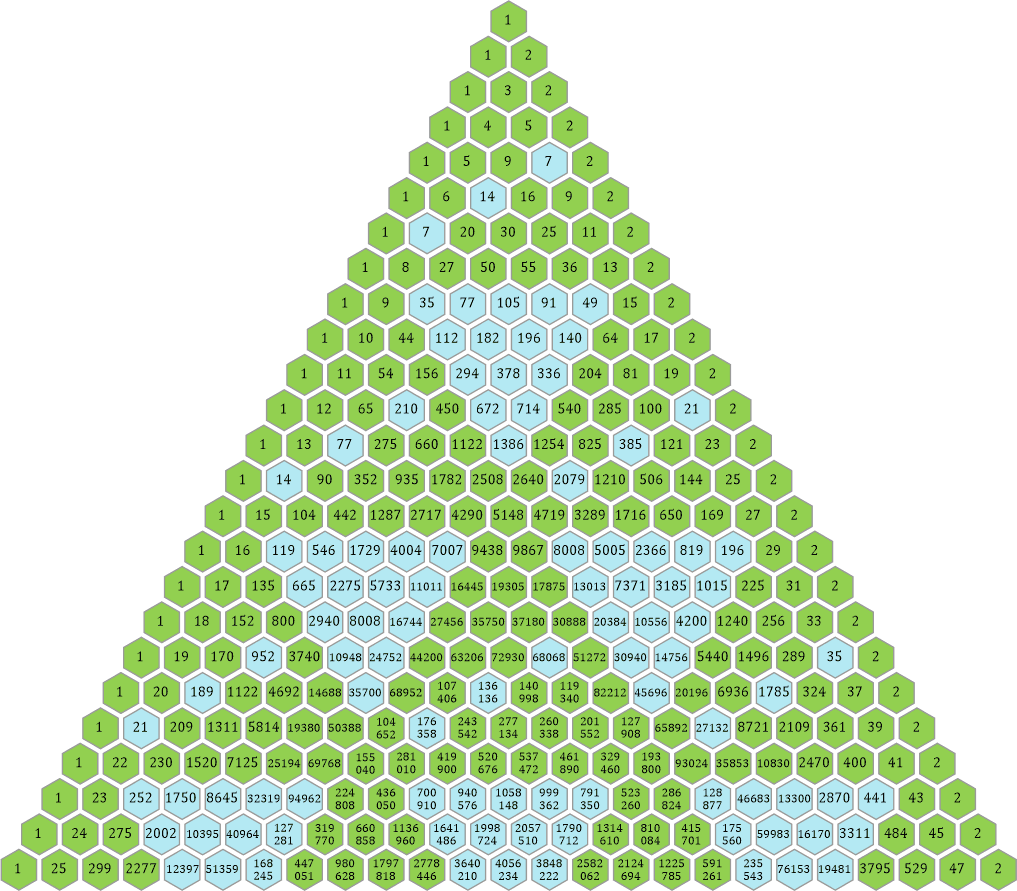
Noch deutlicher sieht man sie im 11er-Dreieck:

Bisher haben wir nur Dreiecke betrachtet, in denen jeweils ein einzelner Primfaktor als Teiler hervorgehoben war. Wie sehen nun Dreiecke aus, in denen zusammengesetzte Primfaktoren hervorgehoben werden?
Als Beispiel nehme ich ein Dreieck, in dem alle Zahlen, die durch 5 ⋅ 7 = 35 geteilt werden können, blau eingefärbt sind. Zuerst im Pascalschen und anschließend im Phi-Dreieck.
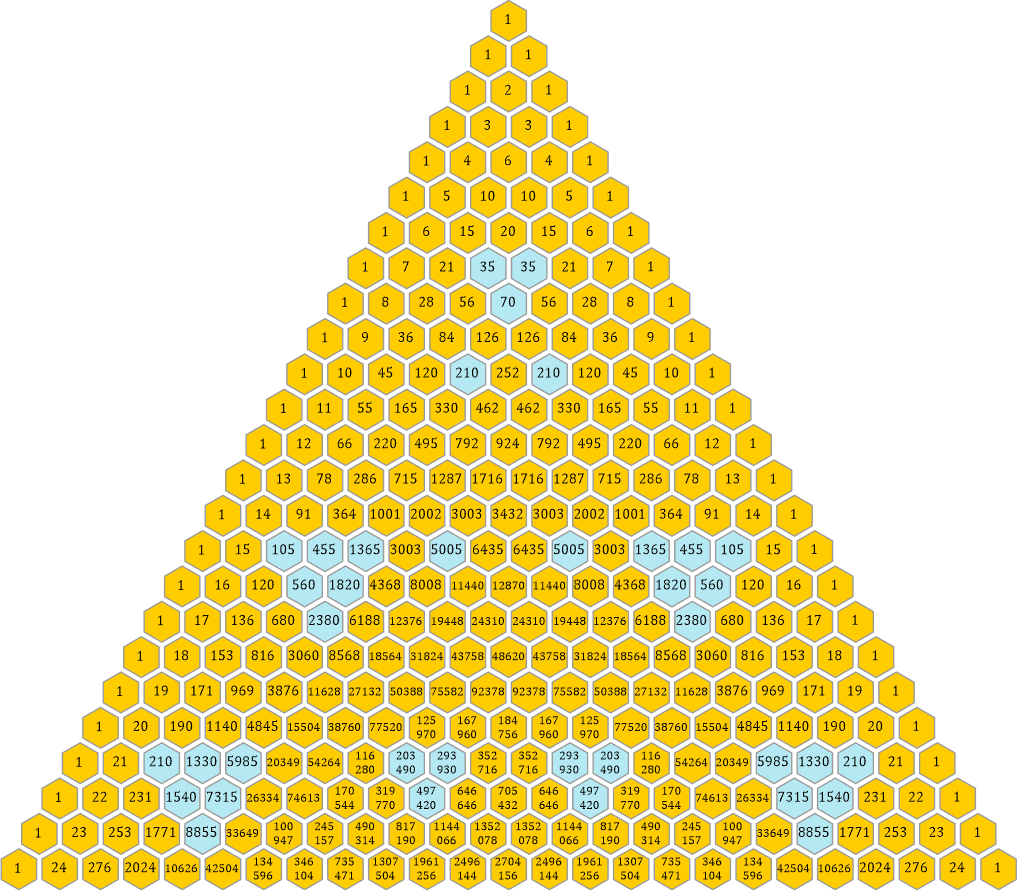
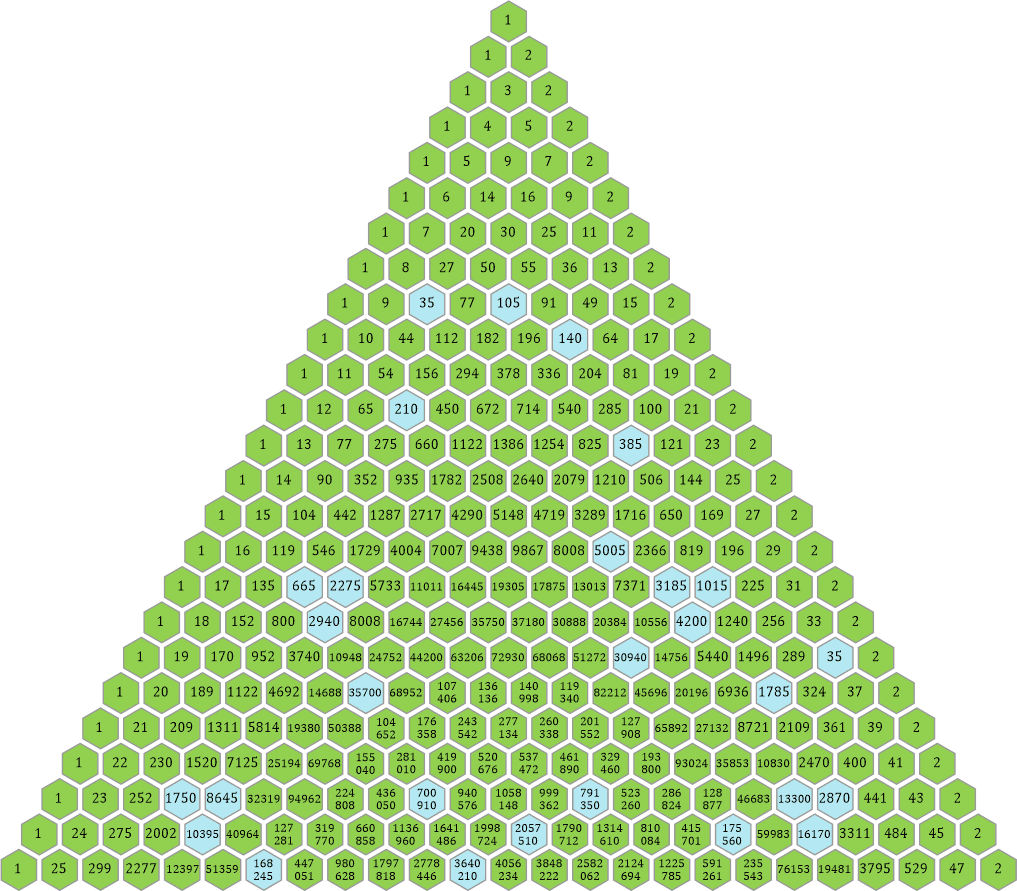
Der Faktor 35 entsteht durch eine »Überlagerung« der Dreiecke mit den Faktoren 5 und 7. Man legt einfach zwei solche Dreiecke übereinander und markiert im Ergebnis nur jene Waben, bei denen sowohl die 5 als auch die 7 hervorgehoben sind. Damit man sie unterscheiden kann, habe ich im 5er-Dreieck die Dreiecke blau belassen, beim 7er-Dreieck habe ich die hervorhobenen Waben mit roten Rändern versehen:
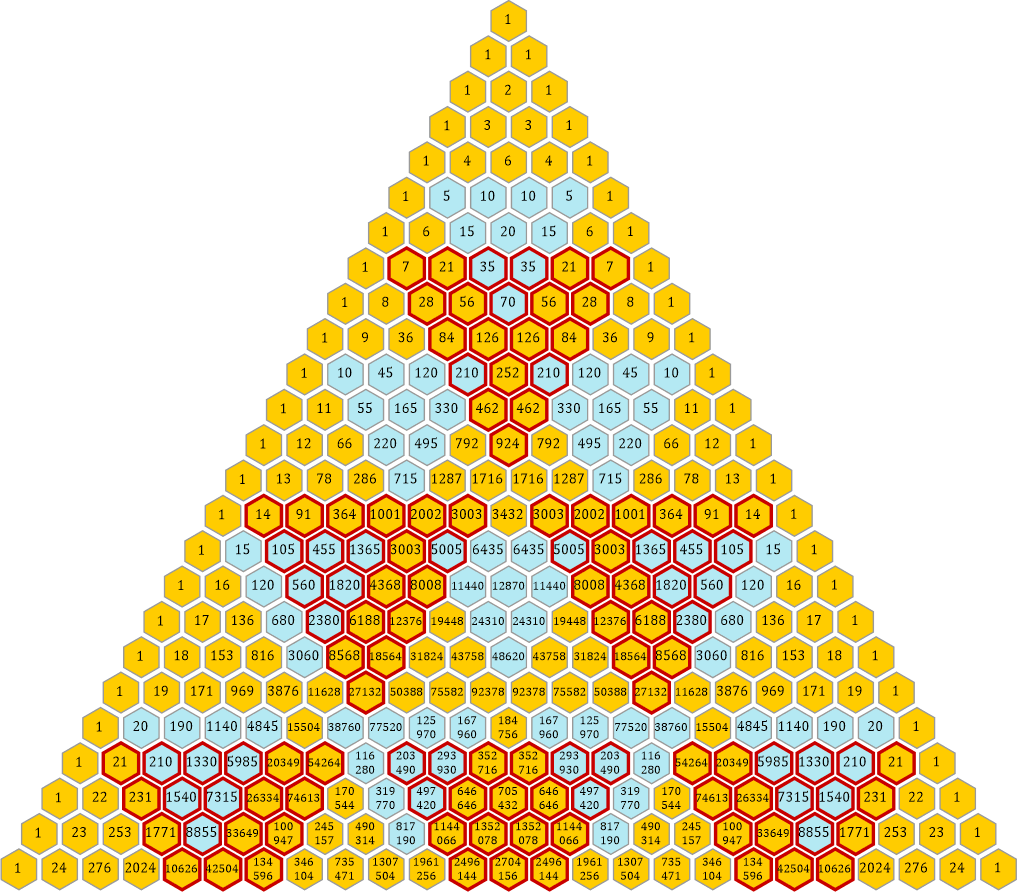

Warum mache ich mir die Mühe, das so ausführlich zu beschreiben? Das Pascalsche Dreieck ist ja schon seit langer Zeit bekannt – gibt es hier noch unbekannte Dinge zu entdecken?
Ja, die gibt es. Und zwar eine ganze Menge! Insbesondere das Phi-Dreieck ist meines Wissens nach bisher überhaupt nicht bekannt. Und das ist ja nichts anderes als zwei minimal verschoben überlagerte Pascalsche Dreiecke ...
Das Phi-Dreieck enthält ein Geheimnis, das nicht nur die Mathematiker interessieren wird, sondern noch viel mehr die Physiker. Denn es schwingt! Es schwingt mit allen Frequenzen, die das Universum zu bieten hat.
Im nächsten Kapitel werde ich diese Schwingungen sichtbar machen.
| 1 | Mit der kleinen Einschränkung, dass das Phi-Dreieck rechts außen ausschließlich aus 2ern besteht, die streng genommen natürlich ebenfalls Primzahlen sind. |
Diese Seite herunterladen: PDF ODT
 |
||