 |
Inhalt • Suchen |  |
2020-11-29
Lückenlos stetig?
Funktionen sind in der Mathematik etwas sehr Wichtiges. Sie sind eine Abbildung der gegenseitigen Beziehung von zwei (oder auch mehreren) Mengen. Um eine solche Beziehung anschaulich darzustellen, kann ich beispielsweise eine Tabelle mit mehreren Elementen der einen Menge und daneben die jeweils zugehörigen Elemente der anderen Menge erstellen. Ein Beispiel sei eine quadratische Beziehung wie y = x2. Diese würde in Tabellenform so aussehen:
| x | y |
| 0 | 0 |
| 1 | 1 |
| 2 | 4 |
| 3 | 9 |
| 4 | 16 |
| ⋮ | ⋮ |
Die Abbildung ist sehr einfach zu erstellen, hat aber einen nicht unwichtigen Nachteil: Sie ist nicht sehr »anschaulich«. Und nebenbei kann man aus der Tabelle nicht ersehen, wie etwaige »Zwischenwerte« (z. B. bei x = 0,17356 oder x = 3,3904) aussehen.
Besser geeignet und weitaus »anschaulicher« sind grafische Abbildungen in Form einer Kurve:
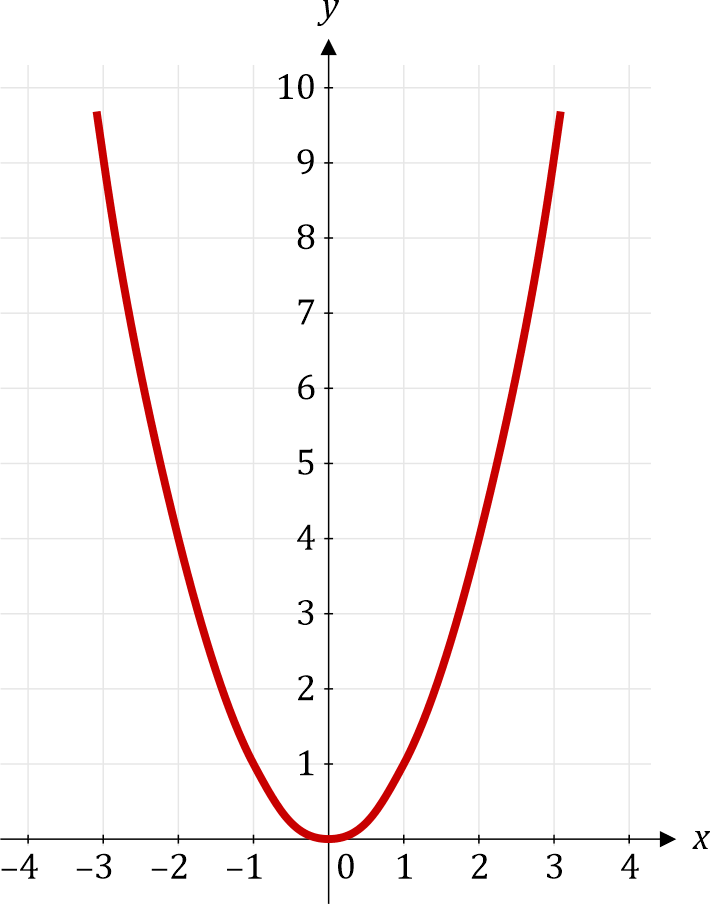
Die rote Kurve zeigt uns auf einen Blick, dass es sich hier um eine stetige Funktion handelt, die man »ohne den Stift abzusetzen« zeichnen kann. Und es gibt auch keinen Zweifel über die Größenordnung von Werten zwischen den ganzen Zahlen, die in der Tabelle aufgelistet sind. Kurven-Abbildungen haben sich sehr bewährt!
Natürlich ist es so, dass wir sowohl in unserer Tabelle als auch in der kurvenförmigen Abbildung nur einen bestimmten »Wertebereich« sehen, nämlich den Bereich zwischen x = 0 und x = 4 in der Tabelle, sowie den Bereich zwischen etwa x = –3,1 und x = +3,1 in der Kurven-Darstellung. Den gesamten Bereich der Funktion können wir ohnehin nicht abbilden, denn x und erst recht y können beliebig große Werte annehmen. Es ist Aufgabe der Mathematiker, uns zu erklären, wie sich eine Funktion auch weit außerhalb eines darstellbaren Bereiches verhält.
Bei einer so einfachen Funktion wie in unserem Beispiel ist eine weitergehende Erklärung nicht wirklich nötig, da es intuitiv einleuchtend ist, dass sich die Funktion »außerhalb« der beiden Abbildungen weiterhin ähnlich verhält. Die Kurve wird einfach noch steiler und die Werte für y wachsen in der Tabelle zunehmend schneller im Vergleich mit den x-Werten. Aber es wird definitiv keine »Sprünge« oder sonstige Anomalien geben, die Kurve ist eine kontinuierliche, man muss den Stift nie absetzen, um sie vollständig zeichnen zu können.
Das ist aber natürlich nicht bei jeder Kurve so. Nehmen wir ein weiteres Beispiel, ein ähnlich einfaches:
| y = |
|
Die Abbildung in Form einer Tabelle würde so aussehen (diesmal in einer etwas höheren Auflösung in Schritten von 0,2 in der Spalte x):
|
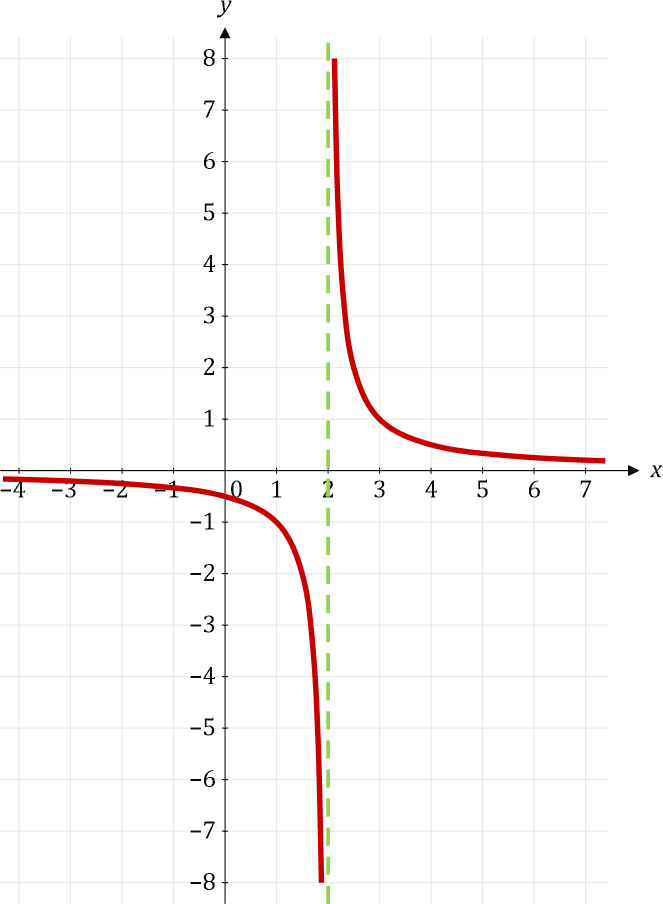 |

DanebenDarunter das entsprechende Abbild in Form einer Kurve. In der rechten Spalte der Tabelle mit den y-Werten steht in der Zeile bei x = 2 ein rotes Fragezeichen. An dieser Stelle nimmt y den Wert unendlich an. Aber welches Unendlich? Plus oder minus – das ist hier die Frage. Wir können sie aber nicht eindeutig beantworten, denn beides ist möglich. Je nachdem, von welcher »Seite« wir uns dieser Stelle nähern, geht der Wert entlang der grün strichlierten Linie gegen +∞ oder –∞. Aber wie groß ist der Wert genau an der Stelle, an der x = 2 ist? Da sich die Frage nicht eindeutig beantworten lässt, lösen Mathematiker dieses Dilemma, indem sie sagen, der Wert von y an dieser Polstelle wäre undefiniert.
Das Problem ist sehr typisch für »lineare Mathematik« – Probleme dieser Art gibt es wirklich viele. Divisionen durch 0 sind der größte Feind jeder Mathematik – und erst recht für eine »angewandte Mathematik«, wie sie in der Physik gebraucht wird. Physiker mögen keine Formeln, die an irgendwelchen Stellen zu einer Division durch 0 führen – verständlicherweise.
Ein weiteres Beispiel einer Kurve, die intuitiv als kontinuierlich empfunden wird, ist die Kurve der Tangens-Funktion. Der Tangens ist nichts anderes als der Wert einer Steigung, also das Verhältnis der zunehmenden Höhe je horizontaler Wegstrecke:
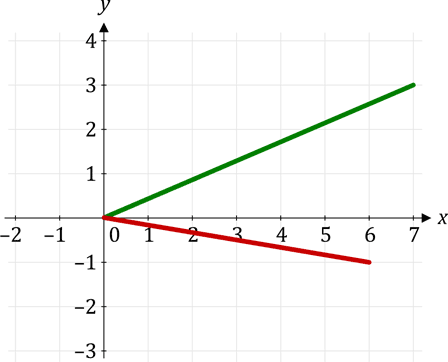
Die grüne Kurve weist eine Steigung (hier mit m bezeichnet) von
| m = |
|
= |
|
≈ | 0,4286 |
auf. Die rote Kurve unterhalb davon hat eine Steigung (bzw. Gefälle) von
| m = |
|
≈ | −0,1667 |
Die meisten von uns, die sich ein wenig mit Mathematik beschäftigt haben, kennen die Tangens-Funktion in Form einer Winkel-Funktion. Fragt man jemanden, was die Tangens-Funktion sei, so ist die Wahrscheinlichkeit hoch, dass die Antwort in etwa »Das ist das Verhältnis von Sinus zu Cosinus« lautet.
Und diese Antwort ist natürlich ebenso richtig. Denn für einen Punkt P auf einem Kreis mit dem Radius von r = 1 entspricht der Sinus dessen y-Komponente (grün) und der Cosinus dessen x-Komponente (rot):
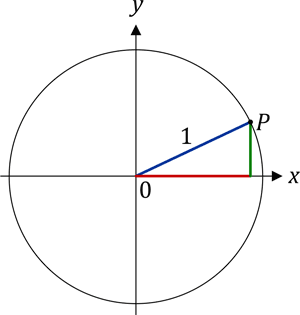
Stellen wir uns nun vor, der Punkt P wäre auf dem Kreis befestigt. Und nun drehen wir den Kreis ein wenig gegen den Uhrzeigersinn:
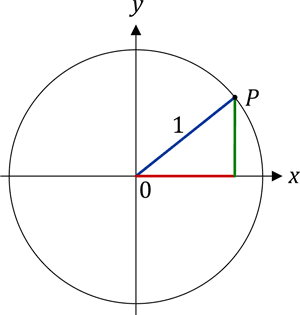
Das Verhältnis von Sinus zu Cosinus, also der Tangens, ist nun etwas größer geworden, da der grüne Wert zugenommen hat, während der rote Wert kleiner geworden ist. Eine weitere kleine Drehung zeigt das noch besser:
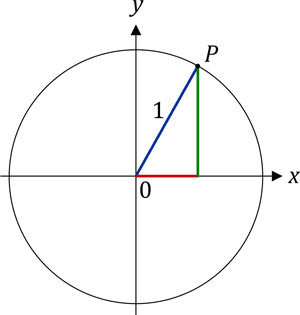
Und während wir noch ein wenig weiter drehen, nähert sich der Punkt P der Stelle, an der die blaue Linie senkrecht steht:
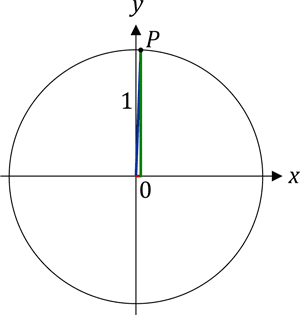
Die grüne und die blaue Linie sind nun fast gleich lang, während die rote Linie nur noch eine winzig kleine Länge aufweist. Was das bedeutet, wenn wir nun die Steigung der blauen Linie berechnen wollen, ist ziemlich offensichtlich: Der Wert der Steigung m ist sehr groß geworden! Und wenn wir jetzt noch ein ganz klein wenig weiterdrehen, dann steht die blaue Linie genau senkrecht und die rote Linie ist verschwunden – sie hat nur noch die Länge 0. Der Wert für den Tangens errechnet sich an dieser Stelle wie folgt (ich verwende jetzt eine etwas andere Schreibweise und verwende für die Länge der grünen Linie den Ausdruck sin für Sinus und cos für Cosinus):
| tan = |
|
= |
|
= | ±∞ |
Ganz, ganz wenig weitergedreht wird der Wert dann plötzlich negativ – wir kennen das schon von unserem zweiten Beispiel, da gibt es einen wirklich wilden Sprung von +∞ nach –∞ an einer einzigen Stelle.
Nun treten wir einen einzigen Schritt zur Seite, nur einen einzigen Schritt. Wir bleiben bei unserer mathematischen Sichtweise, beziehen aber unsere »Realität« mit ein – die Physik. Wir sehen uns dasjenige an, das wir uns »konkret« ansehen können: Unser Universum, das aus lauter einzelnen »Elementarteilchen« aufgebaut ist. Es ist mir an dieser Stelle nicht wichtig, ob es diese »Teilchen« tatsächlich als materielle »Teilchen« gibt, aber das, was wir tatsächlich erkennen und auch »messen« können, ist das Vorhandensein von »Quanten«, also den kleinstmöglichen Einheiten physikalischer Objekte. Diese sind nun mal ganzzahlig abzählbar. Halbe Quanten gibt es nicht. Ein Quantum entspricht der Menge »1«.
Wir stehen also hier auf unseren beiden Beinen, das eine immer noch im Bereich der Mathematik, das andere auf physikalischem Terrain. Und rund um uns dieses unglaublich große Universum, das aus vielen, vielen »Quanten« zusammengesetzt ist. Und jetzt berechnen wir den Tangens eines Winkels zwischen zwei weit entfernten Quanten. Wir sehen da vorne, irgendwo im Inneren des Andromeda-Nebels (unserer Nachbar-Galaxie) ein ganz bestimmtes Elektron A und auch da hinten, ganz in unserer unmittelbaren Nähe, einen Meter schräg neben uns, ein weiteres Elektron B. Der Punkt, an dem wir stehen, ist der Punkt C.
Will ich diese Situation aufzeichnen, so habe ich ein Problem. Denn die Entfernung zwischen den Punkten B und C ist unglaublich winzig im Vergleich zu den Abständen zwischen den Punkten A–B und A–C.

Unsere Nachbar-Galaxie ist etwa 2,5 Millionen Lichtjahre von unserem Punkt C entfernt. Ein Lichtjahr entspricht einer Entfernung, für welches Licht (im Vakuum) ein ganzes Jahr braucht, um sich über diese Entfernung zu bewegen. Licht bewegt sich innerhalb eines Jahres etwa 9.500.000.000.000.000 Meter weit. Also ist unser Elektron A ungefähr 23.750.000.000.000.000.000.000 Meter vom Punkt C entfernt. Wie genau kann diese Entfernung gemessen werden? Auf einen Meter genau? Nie und nimmer. Der Messfehler zwischen A und C ist ganz sicher weitaus größer als die gesamte Entfernung zwischen B und C. Wirkt sich das auf den zu messenden Winkel aus? Nein, so gut wie gar nicht. Allenfalls viele Stellen rechts vom Komma. Und so genau kann man einen Winkel gar nicht messen ...
Messen wir nun die Entfernung zwischen B und C. Hier sieht die Sache mit dem Messfehler sehr viel besser aus. Denn schließlich ist es heute wirklich nur eine Frage des zur Verfügung stehenden Messinstruments, um den Abstand auf den Bruchteil eines Atomdurchmessers genau zu messen. Ein Atom hat einen Durchmesser in der Größenordnung von ungefähr 0,0000000001 Meter (die 1 steht an der 10. Stelle rechts vom Komma).
Wir messen aber nicht den Abstand zu einem Atom, sondern den Abstand zu einem Elektron! Und das ist sehr viel kleiner als ein Atom. Wie groß ein Elektron genau ist, das ist nicht bekannt. Manche Physiker vermuten, es hätte gar keinen Durchmesser, andere geben einen »klassischen« Elektronenradius an (das ist kein gemessener Wert, sondern nur ein errechneter). Aber alle sind sich darin einig, dass man den Ort eines Elektrons, also die genauen Koordinaten des Punktes, an dem es sich zu einem bestimmten Zeitpunkt aufhält, niemals exakt messen kann. Und zwar prinzipiell nicht! Man kann diesen genauen Ort zu einem bestimmten Zeitpunkt nur mit einer gewissen Wahrscheinlichkeit angeben. Also »ungefähr«. Der Messfehler ist unvermeidlich, er ist immer vorhanden! Nichts im gesamten Universum, vom Allerkleinsten bis zum Allergrößten, kann exakt gemessen werden. Es kann niemals ein Messgerät gebaut werden, das über ein gewisses Maß hinaus (oder hinein) exakt messen kann. Denn das Messgerät selbst unterliegt dieser »Unschärfe«, wie Werner Heisenberg1) es genannt hat.
Heisenberg hat dafür auch eine Formel gefunden, die bis heute sehr berühmt ist und einen wahren Eckpfeiler der modernen (Quanten-)Physik darstellt – sie wird Heisenbergsche Unschärferelation2) genannt und lautet:
Δx ⋅ Δp ∼ h
Ziemlich unspektakulär – aber damals, vor fast 100 Jahren, ein echter Meilenstein!
Was besagt denn nun diese einfache Formel? Durchleuchten wir sie ein wenig, schauen wir uns zunächst ihre einzelnen Teile an.
Das x steht für den Ort eines Teilchens, das p für dessen Impuls. Der Impuls ist definiert als Masse mal Geschwindigkeit, salopp könnte man auch sagen, es sei der »Schwung« eines Teilchens, den es hat, wenn es sich bewegt.
Die beiden Dreiecke, »Delta« genannt, bezeichnen gewöhnlich eine Differenz, in diesem Fall eine Ungenauigkeit oder Unbestimmtheit – innerhalb der Grenzen dieses Delta ist der Wert unbestimmt.
Die »Wellenlinie« in der Formel bedeutet »ungefähr«. In den meisten mathematischen Formeln befindet sich ein »Ist gleich«-Zeichen (=), hier jedoch gibt es kein exaktes »ist gleich«, keine exakte Übereinstimmung.
Jetzt fehlt uns noch eine Beschreibung des h auf der rechten Seite der Formel. Das h steht für das Plancksche Wirkungsquantum3) und ist mindestens so bedeutend wie die gesamte Formel von Heisenberg. Diese Konstante h gibt das Verhältnis von Energie und Frequenz eines Photons (eines Lichtteilchens) an.
E = h ⋅ f
lautet die Formel dafür, wobei E für die Energie und f für die Frequenz des Lichtteilchens steht. h ist das Quantum, die Anzahl der »Portionen« der Energie. Es kann nur die Werte 1, 2, 3, 4, 5, ... annehmen.
Vielleicht wirst du jetzt sagen, ich habe hier die Zahl 0 vergessen zu erwähnen. Nein, habe ich nicht. Eine Energie der Größe 0 gibt es nicht. Jedenfalls »nicht wirklich«. Es gibt keinen tatsächlich absoluten Nullpunkt. Quantenphysiker wissen das. Aber sie rechnen an vielen Stellen mit Formeln, welche zu Ergebnissen führen, die eine Null enthalten können, und zwar unterhalb des Bruchstrichs. Solche Ergebnisse sind dann natürlich Nonsens. Und dort fangen sie dann an zu »renormieren« (ein anderes Wort für »schummeln«).
Liebe Mathematiker, helft den Physikern! Gebt ihnen Formeln an die Hand, die solche Ergebnisse grundsätzlich ausschließen! Wie wäre es, wenn ihr den Tangens anders berechnen würdet? Oder den Kreis.
Ihr müsstest lediglich dafür sorgen, dass keine Unendlichkeiten entstehen können. Stellt euch mit einem Fuß auf das Territorium der Physiker und betrachtet euch selbst als »angewandte Mathematiker«, also als Mathematiker, die nicht einfach nur abstrakt irgendwelche Formeln austüfteln, sondern ganz konkrete Probleme lösen.
Ich mache euch einen Vorschlag, liebe Mathematiker. Wie wäre es, wenn ihr euch mit dem Gedanken anfreundet, dass diese Unschärfe, wie sie die Physiker seit Heisenberg stets berücksichtigen (müssen), auch grundsätzlich in euren Formeln eingebaut ist. Wenn ich den Tangens von π / 2 berechne, so darf das Ergebnis nicht ±∞ sein, sondern es muss einen ganz konkreten Wert ergeben. Das heißt aber auch, dass es keine 0 mehr geben darf! Eine Division durch 0 darf nicht mehr vorkommen.
Die alten Griechen, Ägypter und Römer kannten keine 0. Es waren die Babylonier, die die 0 erfanden. Die 0 der Babylonier war aber keine wirkliche 0, sie gab nur die »Stelle« in ihrem Sexagesimalsystem4) an. Doch immerhin – die 0 war geboren! Die Ersten, die eine »echte« 0 hatten (zumindest soweit wir das heute geschichtlich nachvollziehen können), waren die Maya. Sie benutzten ein Zahlensystem auf Basis der Zahl 20. Und sie machten etwas, das moderner war als unsere eigene Zählweise. Sie begann mit der 0 zu zählen! Wenn du heute vor dir auf deine Computer-Tastatur blickst, so findest du unsere 10 Ziffern in einer Reihe von 1 bis 0 angeordnet – ich meine hier nicht die Ziffern auf einem eventuellen »Ziffernblock« auf der rechten Seite neben den Buchstaben, sondern die 10 Ziffern oberhalb der Buchstaben. Dort stehen sie in der Reihenfolge 1, 2, 3, 4, 5, 6, 7, 8, 9, 0. Das ist ein kompletter Unsinn – als ob die erste 0 erst nach der 9 käme! Ein alter Maya würde höchst verwundert den Kopf schütteln.
Nun gut, liebe Mathematiker, ich sperre euch jetzt mit den Physikern für ein Weilchen in einen Raum, solange, bis ihr eine Lösung für das Problem gefunden habt, wie man diese »Unschärfe« oder »Unbestimmtheit« in die Formeln einbauen kann, die bisher zu Nullen unterhalb des Bruchstrichs geführt haben. Und als Lektüre gebe ich euch alle Bücher mit, die sich mit der irrationalsten aller irrationalen Zahlen beschäftigen, der Zahl Φ.
Und dann müsst ihr gemeinsam herausfinden, wie man eine »Überlagerung« (die Physiker sagen dazu auch »Superposition«) mathematisch darstellen kann. Wie man zu Formeln kommt, die 0 und 1 gleichzeitig erzeugen. Also Formeln, bei denen man nicht wirklich sagen kann, was denn nun das »richtige« Ergebnis sei.
Quantenphysiker rechnen stets auf der Basis von Wahrscheinlichkeiten. Ein Teilchen ist jeweils nur mit einer gewissen Wahrscheinlichkeit an einem bestimmten Ort oder zu einem bestimmten Zeitpunkt zu finden. Und diese Wahrscheinlichkeit ist unmittelbar mit jener Unschärfe verknüpft, mit denen die Physiker immer dann konfrontiert sind, wenn sie sich mit »dem Kleinsten« beschäftigen.
Physiker haben ein weiteres Problem. Sie können »das Größte« nicht wirklich mit »dem Kleinsten« in Verbindung bringen. Quantenmechanik und Allgemeine Relativitätstheorie passen nicht gut zusammen. Die Allgemeine Relativitätstheorie Einsteins ist jene, die die Gravitation mit berücksichtigt – und somit auch »beschleunigte Bezugssysteme«. Denn Beschleunigung und Gravitation kann man nicht voneinander trennen – »träge« und »schwere« Masse sind identisch.
Die Gravitationskraft ist die mit sehr großem Abstand kleinste Kraft im gesamten Universum. Sie wirkt immer und überall, über beliebige Entfernungen hinweg, und sie sinkt mit dem Quadrat des Abstands der Körper, die sie verursachen.
Die mit großem Abstand stärkste Kraft im gesamten Universums, welche eine ebenso unbegrenzt große Reichweite hat und ebenfalls mit der gleichen Gesetzmäßigkeit des Abstands zum Quadrat sinkt, ist die magnetische Kraft.
Liebe Physiker und liebe Mathematiker – ist das nicht auffällig? Ich gebe euch den Tipp, einfach mal so zu tun, als ob die beiden Kräfte unmittelbar etwas miteinander zu tun haben könnten.
Wenn ich das Verhältnis von etwas sehr Großem zu etwas sehr Kleinem bilde, dann entsteht daraus etwas, das entweder zum Quadrat größer oder zum Quadrat kleiner ist, je nachdem, ob das Große oberhalb oder unterhalb des Bruchstrichs steht.
Ein Beispiel: G ist das Große, nehmen wir dafür die Zahl 1.000.000, also eine Million. Und K ist das Kleinste, nehmen wir dafür die Zahl 0,000001, also ein Millionstel. G und K stehen also zueinander in einem Verhältnis von
|
= |
|
= |
und das ist nichts anderes als
1.000.0002 = 1.000.000.000.000
Umgekehrt wechselt nur das Vorzeichen im Exponenten:
|
= |
|
= |
Sehen wir uns das Große näher an. Könnte es sein, dass es aus lauter Kleinem besteht? Du wirst das nicht verneinen. Auch wenn du Physiker bist, wirst du es nicht verneinen. Wenn ich dir aber nun sage, dass das Große das Kleine ist, dann wirst du mir wohl den Vogel deuten ...
Ich gebe dir nun ein weiteres Bild. Du kennst vermutlich eine sog. Möbiusschleife, auch Möbiusband genannt. Das ist ein zweidimensionaler Körper, der allerdings nur eine Oberfläche hat. Normalerweise haben zweidimensionale Körper zwei Oberflächen. Ein Blatt Papier als Beispiel für einen zweidimensionalen Körper (ich vernachlässige hier die »Dicke« des Papiers) hat eine Vorder- und eine Rückseite, somit zwei Oberflächen.
Ein Möbiusband kann man auf einfache Weise selber herstellen. Man nimmt ein Blatt Papier und schneidet einen schmalen Streifen davon ab. Diesen Streifen klebt man anschließend an seinen beiden schmalen Enden zusammen, aber so, dass er dabei einmal um 180° um seine Längsachse gedreht wird.
Du wirst sehen, der Streifen hat es in sich! Falls du noch nie etwas von einem Möbiusband gehört hast, dann benutze eine Suchmaschine oder gehe gleich auf eine der folgenden Seiten:
www.vismath.eu/de/blog/das-moebius-band/
www.mathematik.de/dmv-blog/2423-möbius-und-das-möbiusband
www.die-bloggerbande.de/moebius/
Als Variante schreibe auf die Vorderseite des Streifens (bevor du ihn zusammenklebst) die Zahl 1.000.000 und auf die Rückseite die Zahl 0,000001. Nach dem Zusammenkleben stehen die beiden Zahlen auf der selben Seite! Denn es gibt ja keine Vorder- und Rückseite mehr, sondern nur noch eine einzige Fläche.
Schneidest du das Möbiusband mit der Schere der Länge nach auseinander, so erhältst du – nein, nicht zwei, sondern wiederum ein einziges Band! Und machst du das anschließend noch einmal, dann erhältst du endlich zwei Bänder. Allerdings sind diese beiden Bänder ineinander verschlungen und du kannst sie nicht voneinander trennen ...
Als Nächstes gebe ich dir ein weiteres Bild. Es ist das Bild einer sog. Normalverteilung, du kennst es auch als Gaußsche Glockenkurve. Und zusätzlich lege ich das Bild eines Pascalschen Dreiecks darunter. Die beiden haben sehr viel miteinander zu tun, das weißt du mittlerweile. Die Glockenkurve ist ein Abbild einer Zeile des Pascalschen Dreiecks.
Diese Glockenkurve entsteht, indem man eine 1 »aufspaltet« und anschließend immer und immer wieder die Ergebnisse der gespaltenen 1 zusammenzählt. Im Artikel Wege habe ich das beschrieben. Hier nochmals das Dreieck, dessen einzelne Zahlen in wabenförmige Sechsecke geschrieben sind, darunter die Glockenkurve für die letzte Zeile:
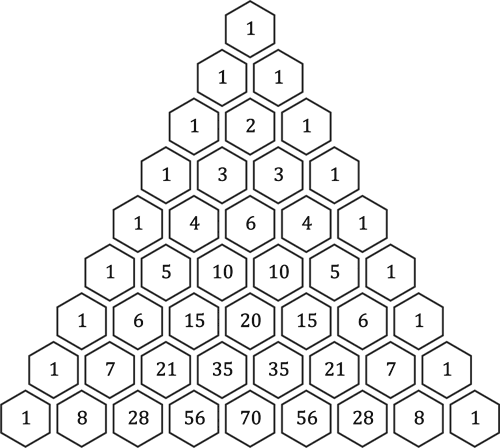
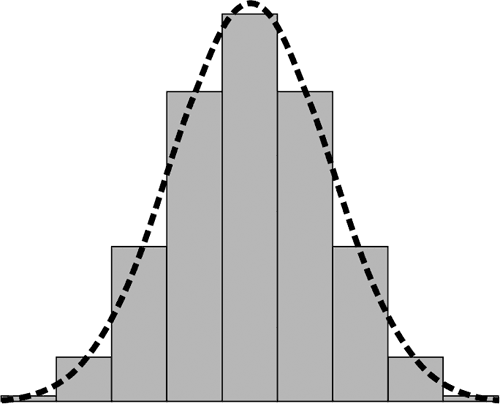
Die einzelnen Balken haben eine Höhe von 1, 8, 28, 56 und 70. Die strichlierte Linie entspricht der »glatten« Gaußschen Glockenkurve, die man erhält, wenn man das Dreieck sehr viel größer zeichnet und dadurch die einzelnen »Treppenstufen« so klein werden, dass sie nicht mehr sichtbar sind.
Man kann die Glockenkurve auch auf eine andere Weise erhalten. Nämlich indem wir sie anstatt durch eine ganze Reihe einzelner Additionen durch eine Reihe von Multiplikationen konstruieren. Die einzelnen Zahlen jeder Zeile des Dreiecks kann ich nämlich auch durch Multiplizieren erzeugen. Und zwar so, dass ich dafür ein etwas abgewandeltes »Möbiusband« verwende. Ich schreibe auf die eine Seite des Bandes die Zahlen 1, 2, 3, 4, 5, 6, 7, 8 und auf die andere Seite des Bandes die gleichen Zahlen. Da die Rückseite aber spiegelverkehrt zur Vorderseite erscheint, wenn wir uns das Band vor unsere Augen halten (und uns das Band als halb durchsichtig denken), erscheinen auf der Rückseite die Zahlen in umgekehrter Reihenfolge: 8, 7, 6, 5, 4, 3, 2, 1. Die ganze Zahlenreihe wird nun miteinander multipliziert. Auf der einen Seite des Bandes erhalte ich
8 ⋅ 7 ⋅ 6 ⋅ 5 ⋅ 4 ⋅ 3 ⋅ 2 ⋅ 1
und auf der anderen Seite
1 ⋅ 2 ⋅ 3 ⋅ 4 ⋅ 5 ⋅ 6 ⋅ 7 ⋅ 8
Dazwischen ziehe ich einen »Bruchstrich« und zwar so, dass ich auch die einzelnen Zwischenergebnisse ablesen kann.
|
⋅ |
|
⋅ |
|
⋅ |
|
⋅ |
|
⋅ |
|
⋅ |
|
⋅ |
|
|
= 8 |
| 8 ⋅ |
|
= 28 |
| 28 ⋅ |
|
= 56 |
| 56 ⋅ |
|
= 70 |
| 70 ⋅ |
|
= 56 |
| 56 ⋅ |
|
= 28 |
| 28 ⋅ |
|
= 8 |
| 8 ⋅ |
|
= 1 |
Du ahnst vermutlich bereits, worauf ich hinauswill. Aber vorher gilt es noch einen kleinen »Schönheitsfehler« zu korrigieren. Denn ganz links fehlt noch eine 1, das Dreieck ist schließlich symmetrisch und hat auf beiden Seiten jeder Zeile immer eine 1. Den »Fehler« korrigiere ich, indem ich die beiden »Enden« miteinander verbinde. Zur linken Formel füge ich ganz außen noch einen Faktor 1 dazu, sodass sie anschließend so aussieht:
| 1 ⋅ |
|
= 8 |
Und anschließend »klebe ich die beiden Enden zusammen«, sodass sie einen Kreis ergeben – ein »Möbiusband«. Die linke und die rechte 1 im Pascalschen Dreieck darf ich getrost überlappen, sodass ich hier eine gute »Klebestelle« für das Zusammenkleben der beiden Enden des Bandes habe. Die 1 am oberen Ende des Dreiecks ist ja schließlich auch nichts anderes als eine »Überlappung« von zwei Einsen. Und das Band wird zu einem Möbiusband, da ich es beim Zusammenkleben einmal umdrehen muss, sodass die
|
und die |
|
so zu liegen kommen, dass die jeweiligen Zahlen ober- und unterhalb des Bruchstrichs sich schön decken.
Das Gesamtbild, das ich hier zeichne, beginnt nun bereits besser sichtbar zu werden. Wir sind von dem Problem ausgegangen, dass an der »Kippstelle« der Tangens-Funktion die Linie plötzlich von der einen auf die andere Seite springt (von +∞ nach –∞). Die winzige Kreisbewegung, die das verursacht hat, ist jedoch gänzlich harmlos und »weich« gewesen. Ohne ein Ruckeln, ohne das geringste Zittern.
Auf dem (endlosen) kreisförmigen Möbiusband sind beliebig lange Kolonnen von Natürlichen Zahlen aufgeschrieben, die immerwährend mit sich selbst in gegenläufiger Richtung multipliziert werden – und dabei immer das Ergebnis von genau 1 liefern. Die Vorderseite hat einen positiven Exponenten, die Rückseite hat einen negativen Exponenten – das ist der ganze Unterschied. Und immer entstehen mit jeder Multiplikation schöne ganze Zahlen, nie entsteht dabei eine »Bruchzahl«.
Ein etwas »größeres« Beispiel gefällig? Nehmen wir anstatt der Zahlen 1 bis 8 die Zahlen 1 bis 31. Wer weiß, vielleicht funktioniert es bei größeren Zahlen ja nicht mehr ...
| 1 ⋅ |
|
= | 31 | |||
| 31 ⋅ |
|
= | 465 | |||
| 465 ⋅ |
|
= | 4.495 | |||
| 4.495 ⋅ |
|
= | 31.465 | |||
| 31.465 ⋅ |
|
= | 169.911 | |||
| 169.911 ⋅ |
|
= | 736.281 | |||
| 736.281 ⋅ |
|
= | 2.629.575 | |||
| 2.629.575 ⋅ |
|
= | 7.888.725 | |||
| 7.888.725 ⋅ |
|
= | 20.160.075 | |||
| 20.160.075 ⋅ |
|
= | 44.352.165 | |||
| 44.352.165 ⋅ |
|
= | 84.672.315 | |||
| 84.672.315 ⋅ |
|
= | 141.120.525 | |||
| 141.120.525 ⋅ |
|
= | 206.253.075 | |||
| 206.253.075 ⋅ |
|
= | 265.182.525 | |||
| 265.182.525 ⋅ |
|
= | 300.540.195 | |||
| 300.540.195 ⋅ |
|
= | 300.540.195 | |||
| 300.540.195 ⋅ |
|
= | 265.182.525 | |||
| 265.182.525 ⋅ |
|
= | 206.253.075 | |||
| 206.253.075 ⋅ |
|
= | 141.120.525 | |||
| 141.120.525 ⋅ |
|
= | 84.672.315 | |||
| 84.672.315 ⋅ |
|
= | 44.352.165 | |||
| 44.352.165 ⋅ |
|
= | 20.160.075 | |||
| 20.160.075 ⋅ |
|
= | 7.888.725 | |||
| 7.888.725 ⋅ |
|
= | 2.629.575 | |||
| 2.629.575 ⋅ |
|
= | 736.281 | |||
| 736.281 ⋅ |
|
= | 169.911 | |||
| 169.911 ⋅ |
|
= | 31.465 | |||
| 31.465 ⋅ |
|
= | 4.495 | |||
| 4.495 ⋅ |
|
= | 465 | |||
| 465 ⋅ |
|
= | 31 | |||
| 31 ⋅ |
|
= | 1 |
Wenn man genau hinschaut, erkennt man leicht, warum hier nie Bruchzahlen entstehen können. Ich erkläre das hier nicht im Detail, da es offensichtlich ist – und überlasse es dir selbst, es zu erkennen. :-)
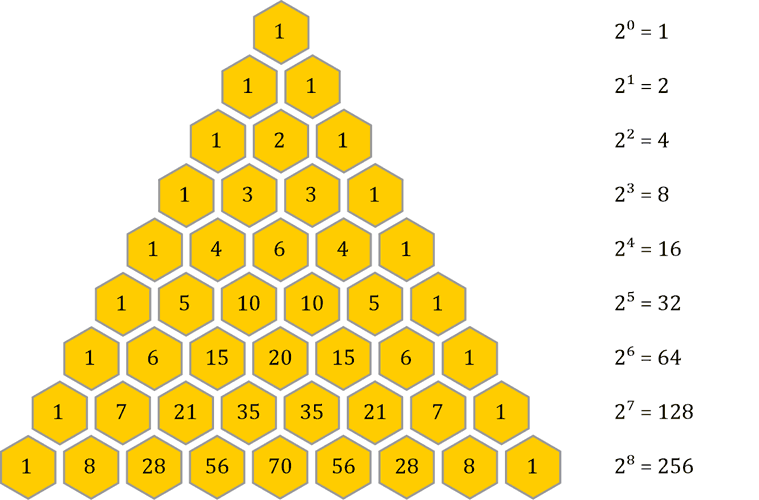
Neben mir steht mein mathematischer Zauberkasten und ich krame ein wenig darin – – – hmm, was haben wir denn da? Schon wieder ein Pascalsches Dreieck. Hab wohl versehentlich zwei eingepackt. Macht nix. Legen wir es zum anderen dazu. Legen wir die beiden Dreiecke übereinander. Wir können sie gut unterscheiden, denn das eine Dreieck ist gelb eingefärbt und das andere blau:

Irgendwie erinnert mich dieser Anblick an etwas – – – zwei Zahlen, die übereinanderliegen – könnte man das als »Überlagerung« bezeichnen? Nein, das ist bestimmt ein Blödsinn. Aber macht ja nichts, man kann ja mal versuchen, was dabei herauskommt, wenn ich aus den beiden »überlagerten« Dreiecken ein neues »Summen-Dreieck« mache. Ich zähle einfach die jeweils übereinanderliegenden Zahlen zusammen – ok?
Das grüne Dreieck ist das Ergebnis – jetzt weiß ich auch, warum mir dieser Anblick bekannt vorgekommen ist. Das Ergebnis ist nichts anderes als das Dreieck, das ich vor längerer Zeit »Phi-Dreieck« genannt habe. Die linke Reihe mit den 1ern des gelben Dreiecks habe ich natürlich so belassen, da hier keine Überlagerung besteht. Die unterste Zeile des blauen Dreiecks habe ich weggelassen, da mir hierfür die Zahlen des gelben Dreiecks fehlen.
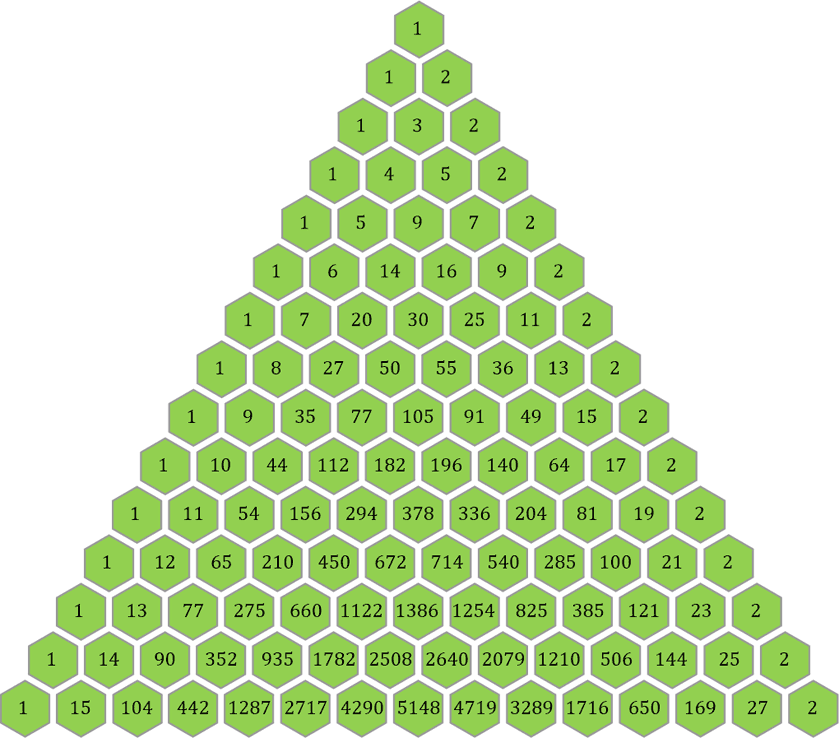
Wenn du in »Werden« zur Tabelle 4 blätterst, wirst du dieses Dreieck allerdings in einer etwas anderen Form finden:
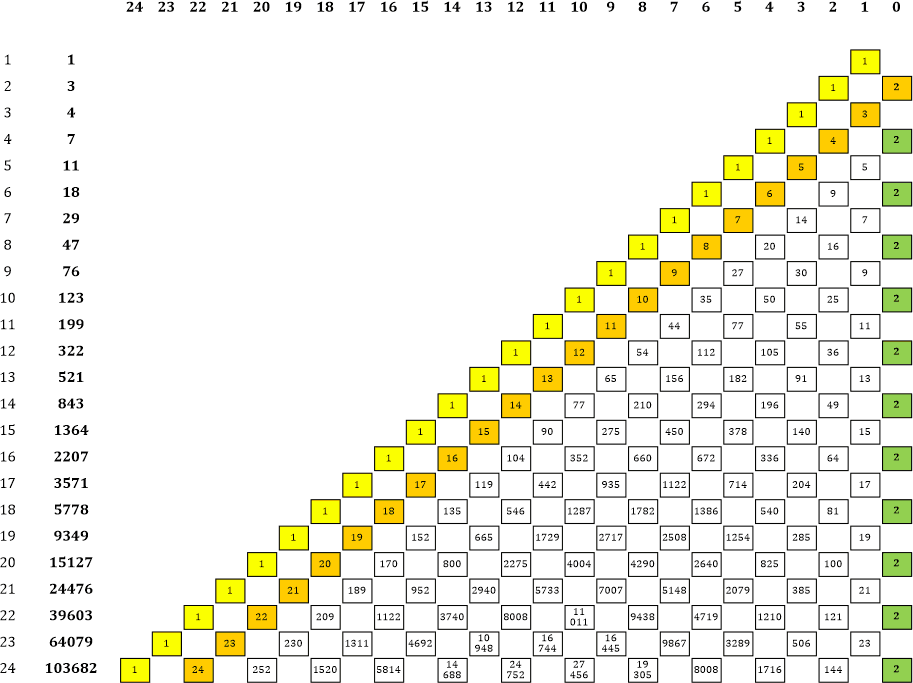
Links hatte ich die Quersummen der einzelnen Zeilen hingeschrieben und dabei die Zahlen der Lucas-Folge erhalten. Beim grünen Dreieck, das »kompakter« ist und die Zahlen nicht innerhalb von Rechtecken sondern innerhalb von 6-eckigen Waben enthält, findet man diese Quersummen nicht mehr horizontal, sondern um 30° gedreht – siehe violette Waben und rechte Zahlenreihe. Die erste Zahl in der Reihe (2) ist wie üblich »falsch«.
Gleichzeitig findet man im Dreieck auch die Fibonacci-Folge, sie ist um 30° in die andere Richtung gedreht – siehe rote Waben und linke Zahlenreihe.
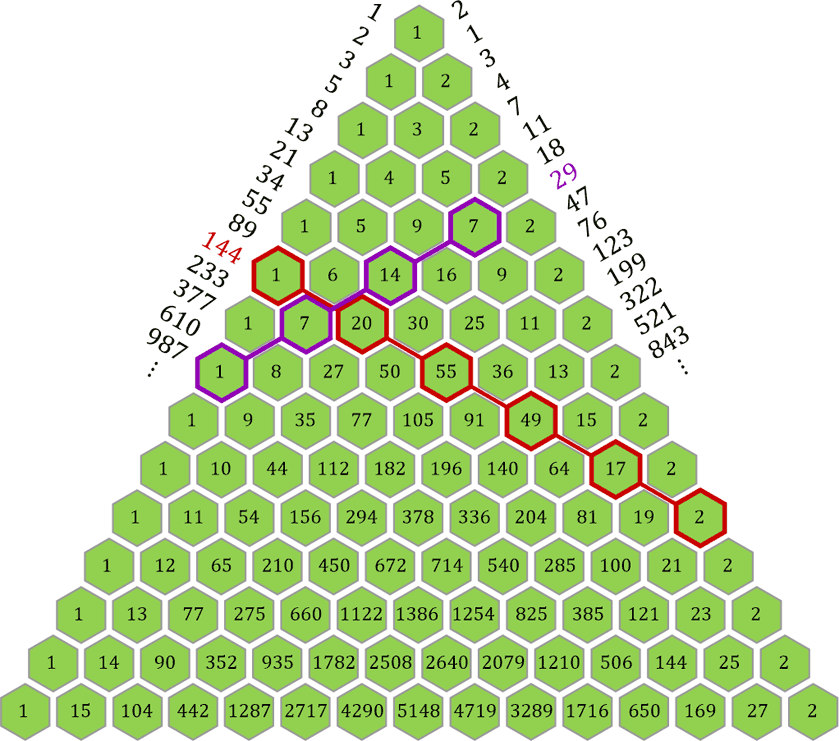
Auch das Pascalsche Dreieck enthält die Fibonacci-Reihe, allerdings in anderer »Zusammensetzung«. Um das sichtbar zu machen, nehme ich mein gelbes Dreieck und zeichne dort ebenfalls mit Hilfe roter Waben die schräge Zeile ein, deren Summe die Fibonacci-Zahl 144 ergibt.
Es ist leicht überprüfbar, dass alle parallelen Zeilen-Summen jeweils die Fibonacci-Zahlen liefern. Die Summe 144 ergibt sich im grünen Dreieck aus der Summe der Zahlen 1 + 20 + 55 + 49 + 17 + 2 = 144 und im gelben Dreieck aus den Zahlen 1 + 10 + 36 + 56 + 35 + 6 = 144.
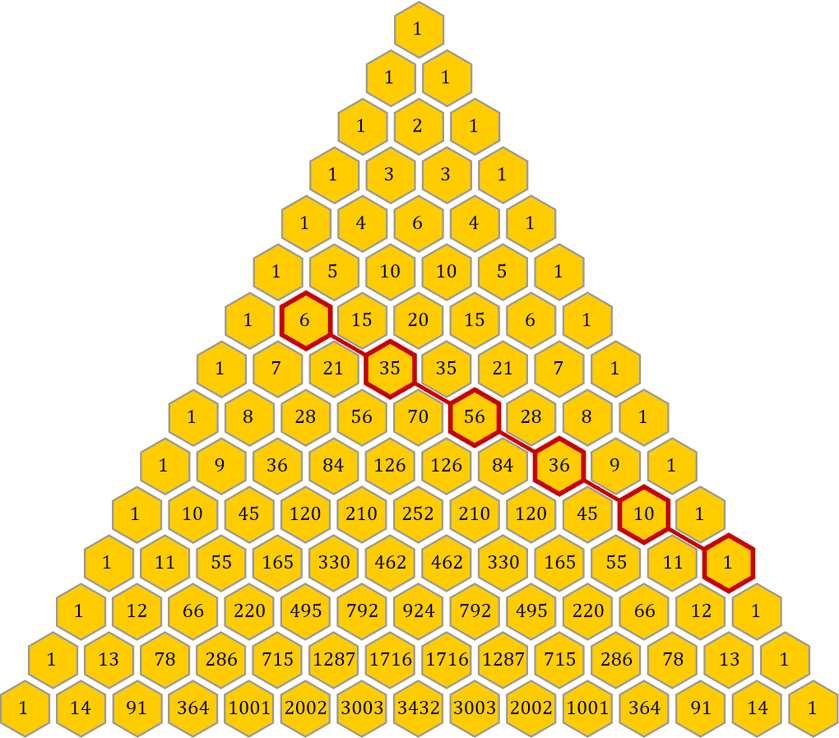
Da das gelbe Pascalsche Dreieck symmetrisch ist, sind die Fibonacci-Zahlen hier natürlich in beide Richtungen zu finden.
Kommen wir zum nächsten Bild. Jeder Physiker kennt den Begriff »Wellenpaket«. Es handelt sich dabei um kein Paket, das man von der Post bekommt, sondern um eine räumlich oder zeitlich begrenzte Welle und sieht zum Beispiel so aus:
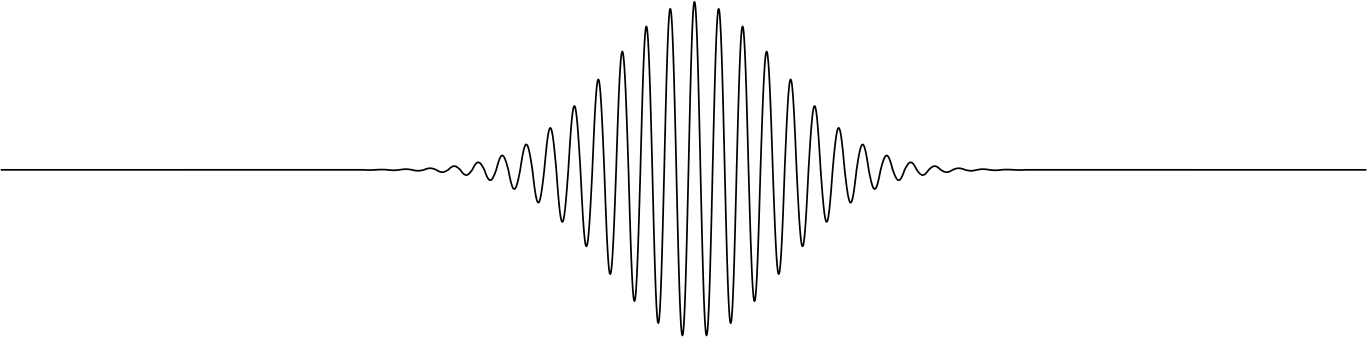
Die »Hülle« dieses besonderen Wellenpakets hat die Form einer Glockenkurve, deshalb wird es auch Gaußsches Wellenpaket genannt. Ein solches Gaußsches Wellenpaket ist gleichzeitig nichts anderes als ein »Teilchen«, ein sog. Elementarteilchen. Letztere Behauptung ist ziemlich gewagt, das ist mir bewusst, aber ich bewege mich damit durchaus in einem »physikalischen Rahmen«. Auf der Website der Technischen Universität Braunschweig findest du einen kurzen Artikel, der nicht allzu hohe mathematische Voraussetzungen verlangt (es wäre aber natürlich vorteilhaft, wenn dir der Begriff »Fourier-Analyse« nicht fremd ist). Der Artikel hat den Titel »Wellenpakete: Aus einer Welle wird fast ein Teilchen«. Ich habe für mich das Wort »fast« gestrichen. Und außerdem ergänze ich das Bild des Wellenpakets noch ein wenig. Die Hüllkurve des Pakets ist eine Glockenkurve. Und eine Glockenkurve wird aus einer Menge von Einzelereignissen gebildet – aus sämtlichen möglichen Wegen, die zu einem bestimmten Ereignis führen. Die Glockenkurve ist die geglättete Form einer »Zeile« des Pascalschen Dreiecks. Oder auch zweier minimal verschobener, überlagerter Dreiecke. Sie besteht aus lauter aneinandergereihten »Balken«, deren obere Enden die Hülle der Kurve bilden – siehe ein Stück weiter oben in diesem Text.
Im Bild 17 von »Werden« siehst du die »Balken« der Hüllkurve in jeder Zeile des Phi-Dreiecks. Sie stehen dort in Form der einzelnen ganzzahligen Terme, die jeweils mit den geradzahligen oder ungeradzahligen Potenzen von Φ multipliziert sind. Indem die Vorzeichen alternieren, also ständig zwischen + und − wechseln, macht es Sinn, die positiven Balken nach oben zu zeichnen und die negativen Balken nach unten. Für die 16. Zeile würde das beispielsweise so aussehen:
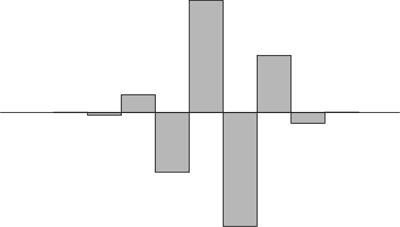
1 − 16 + 104 − 352 + 660 − 672 + 336 − 64 + 2 = −1
(ohne Φ-Potenzfaktoren)
bzw.
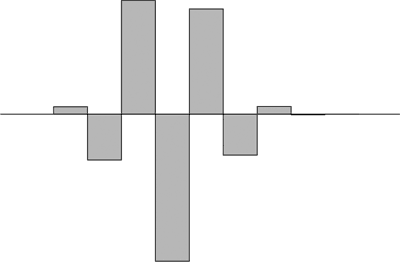
1Φ16 − 16Φ14 + 104Φ12 − 352Φ10 + 660Φ8 − 672Φ6 + 336Φ4 − 64Φ2 + 2Φ0 = −Φ
(mit Φ-Potenzfaktoren)
Der vertikale Maßstab der beiden Balkendiagramm ist wegen einer besseren Darstellbarkeit unterschiedlich gewählt, das Prinzip ändert sich dadurch nicht.
Das Pascalsche bzw. das Phi-Dreieck sind nichts anderes als die Darstellung eines Wellenpakets und somit der Wahrscheinlichkeitswelle eines (Elementar-)Teilchens. Sie bestehen aus der Überlagerung von beliebig vielen Wellen mit lauter unterschiedlichen Frequenzen, wobei die Breite eines Balkens h entspricht, dem Heisenbergschen h, dessen physikalische Dimension einem Drehimpuls(!) entspricht. Teilchen entstehen (»werden«) aus nichts anderem als der »Überlagerung« einzelner Zahlen – aus einer »geteilten 1« im Verhältnis 1 : Φ. Das Wellenpaket ist umso energiereicher, je mehr Balken es enthält. Physiker, du weißt, dass jedes Teilchen aus einem ganzzahligen Vielfachen seiner Quanten besteht. Alles, was konkret vorhanden ist, setzt sich aus einzelnen Quanten zusammen. Und da es keine »halben« Quanten geben kann (sie wären dann keine Quanten mehr), musst du mit den »Treppenstufen« leben. Du wirst nie eine solche Treppenstufe zu sehen bekommen, denn sie sind »unscharf«. Für dich sind es immer glatte Wellen. Die Mathematik erlaubt es dir jedoch, sie aufzulösen. Dann siehst du, dass es nichts Kleineres gibt als die 1. Und es gibt keine Null – Pythagoras, Thales & Co wussten das. Ich bin allerdings unsicher, ob sie wussten, warum. Elementarteilchen entstehen und vergehen vor deinen Augen, sie wandeln sich fast nach Belieben ineinander um, manche von ihnen nennst du virtuell, da sie gar nicht wirklich da sind, aber eben doch da sind – du kennst deinen Zoo und kannst ihn nicht bändigen. Und du weißt, dass es kein wirkliches Vakuum geben kann. Es gibt nicht nichts. Du gibst dem Vakuum manchmal Namen wie »Nullpunktfeld« und Ähnliches, wissend, dass da immer etwas um den Nullpunkt herum »schwingt«. Manchmal ist es da, manchmal nicht. Ein kleines Teilchen hat ein Magnetfeld, das unglaublich stark ist. Deine Formeln sagen, dass seine Stärke mit dem Quadrat des Abstands sinkt. Nun, das ist bestimmt richtig. Wenn der Abstand groß genug ist. Aber ganz nah, unmittelbar nah, da explodieren deine Formeln. Beim Abstand 0, direkt am Nullpunkt wird die Kraft eines Magneten unendlich groß. Und dort beginnst du dann zu schummeln ... Du musst nicht schummeln. Verwende einfach eine etwas andere Mathematik. Nimm nur konkrete, ganze Zahlen, die aus einer einzigen Verhältniszahl zusammengesetzt sind, dann musst du nie wieder schummeln. Denn der kleinstmögliche Abstand ist dann 1. Diese 1 ist genauso breit wie eine von Schrödingers Katzen.
Am »Nullpunkt«, der die Breite von 1 hat, man könnte auch sagen, der die Breite von h hat, ist das Zentrum des Universums. Es befindet sich genau dort, man sieht es aber nur ein wenig unscharf. Das Universum hat so viele Zentren wie es »Teilchen« hat. Ständig entstehen welche und vergehen wieder. Das einzig wirklich Beständige ist die Veränderung. Ständig wird dem Universum Energie zugeführt (ja, du hast richtig gelesen, Physiker!) und ihm wieder Energie entzogen. Das Universum stirbt keinen Wärmetod, Physiker. Und es ist auch nicht durch einen Knall entstanden. Der Knall ist nur in deinem Kopf. Es entsteht jetzt gerade in diesem Moment. Jetzt! Das Brot wird jetzt gebacken!5) Und in der Hexenküche duftet es danach – die Hexe nennt diesen Duft manchmal auch Kosmische Hintergrundstrahlung. Sie tut das aber nur, um die Physiker zu ärgern.
Betrachte das gesamte Universum, Physiker. Lege es auf deine offene Hand, es hat darauf problemlos Platz. Du bist selbst dieses Universum, Physiker, aber du weißt es nicht. Du stehst erst ganz am Anfang einer langen, langen Reise, die du ganz freiwillig angetreten hast. Derzeit lebst du am äußersten Rand der Wirklichkeit, ganz draußen, dort, wo es nur 0 und 1 gibt. Deine Logik lässt noch nicht mehr zu. Doch du kannst sehen, dass die 0 und die 1 gleichzeitig da sind. Und dass dazwischen die Würfel fallen, die Einstein nicht wirklich akzeptieren wollte. Nun, ganz so unrecht hatte Einstein nicht. Einerseits gibt es sie tatsächlich, die Würfel, den Zufall. Andererseits ist alles mit allem verbunden und nichts ist zufällig. Gar nichts.
Weißt du, Physiker, manchmal ist es hilfreich, den Verstand in der Küche der Hexe zu lassen und einfach den Duft ihres Brotes zu genießen. Der Verstand ist sehr dual. Sehr dual. Aber er hat zwei Löcher. Durch das eine kriecht er hinein und durch das andere heraus. Die Schwerkraft ist nichts anderes als das Gegenstück zur magnetischen Kraft. Die elektro-magnetische Kraft wechselt ständig ihre Form von magnetisch zu elektrisch. Wenn sie sich nicht wechselt, ist keine Energie vorhanden. Je schneller sie sich wechselt, desto mehr Energie ist vorhanden. Je mehr Balken das Wellenpaket ... du weißt das. Energie nennst du manchmal auch Masse. Und diese ist schwer – stimmt’s? So ein kleines Teilchen hat jedoch unglaublich wenig Masse und ist daher entsprechend wenig schwer. Seine »Anziehungskraft« ist unglaublich klein. Dennoch wird sie unendlich groß, wenn du den Radius deines Teilchens gegen null gehen lässt. Du hast das längst verstanden und weißt um die Unschärfe, und dadurch hast du dieses Problem beseitigen können. Aber die Unschärfe selbst hast du noch nicht wirklich verstanden.
Du hast das Pferd von der falschen Seite bestiegen. Du hast die Dimensionen von »unten« aufgebaut. So wie auch ich es vor 40 Jahren versucht hatte. Ich habe damals bei 7 Dimensionen Schluss gemacht. Deine Kollegen von der »String-Fraktion« sind da weiter gegangen, mindestens bis zu 11. Und sie haben ein unglaublich kompliziertes Gebilde errichtet, das ein Kartenhaus ist. Diejenigen, die ihren Verstand manchmal für ein paar Augenblicke in die Schublade der Hexe legen, ahnen manchmal, dass es tatsächlich ein Kartenhaus ist. Aber dann nehmen sie schnell wieder ihren Verstand heraus und bauen weiter an dem Kartenhaus. Es ist jetzt 11 Stockwerke hoch.
Hör mal der Stimme aus dem Jenseits zu. Heimlich. Du musst es ja niemandem deiner Kollegen sagen, dass du den »Feindsender hörst«. Er erzählt dir, dass es jenseits der 4 Dimensionen nichts gibt außer – Multidimensionalität. Alles mit allem. Eins!6)
Du kannst auch den alten Weisen zuhören. Die sagten immer schon, dass die Materie nur Maya ist. Ein Trugbild. Selbst dein Verstand ist ein Trugbild. Wie sollte er auch etwas anderes sein, ist er doch »linear« – ein Gedanke nach dem anderen. Sein Ergänzungsstück ist die Intuition. Alles gleichzeitig. Und das Dritte in diesem Reigen, das Herz, die Liebe, hält alles im Gleichgewicht.
Intuition, das geht ja noch. Gerade noch. Zumindest ein bisschen. Aber Liebe? Nicht für einen Physiker. Kompletter Blödsinn.
Es ist nichts anderes als das Gegenüber des Verstands. Alles in diesem Universum ist paarweise vorhanden: actio = reactio. Aber manche Paare sind multidimensional. So wie die Gravitation und der Magnetismus. Sie sind beide beliebig weit zu spüren, quadratisch abnehmend mit der Entfernung. Aber sie stehen zueinander auf dem Kopf. Wie Schrödingers Katzen.
Jede Galaxie hat zwei Ventile. Ein »Einlassventil« und ein »Überdruckventil«. Eines ist riesengroß und unübersehbar (weil es nicht zu sehen ist) und das andere ist winzig klein und daher ebenfalls nicht zu sehen. Obwohl es so viele davon gibt.7)
Entropie – ein neues Stichwort. Das Maß für die »Unordnung«. Du weißt, Physiker, dass zum Zeitpunkt deines Urknalls die Entropie praktisch null gewesen sein muss und seither ständig zunimmt. Ein sich selbst überlassenes System »zerfällt«. Bei deinem Urknall war alles in bester Ordnung und seither entsteht immer mehr Unordnung. Weißt du, warum das so ist? Weil du von einem toten Universum ausgehst. Für dich ist alles tot! Alles. Und das bisschen Leben, das du nicht leugnen kannst (dich selbst zu leugnen bringst nicht einmal du zustande), ist purer Zufall. Purer Zufall.
Leben findet zwischen den Würfeln statt. Es kommt durch die vielen Einlassventile herein und wird wieder abgesaugt durch das große unübersehbare Loch, das man nicht sehen kann.
Es gibt nichts Totes, Physiker. Nichts! Das kleinste Elektron ist so voll von Leben, dass du ein ganzes Universum benötigst, um es auszufüllen. Ich hoffe, du hast deinen Verstand bei der Hexe gelassen, um das zu verstehen ...
Lebewesen bestehen aus einzelnen Zellen. Größere Lebewesen bestehen aus vielen Zellen. Im Falle eines Menschen gibt es über den Daumen gepeilt an die 100 Billionen davon. Jede Zelle unterscheidet sich von der anderen. Aber sie sind alle unverwechselbar »codiert«, vollkommen identisch. Mit einem Code, den kein anderes Lebewesen im gesamten Universum hat. Der Code windet sich. Doppelsträngig. Es ist ein Steuerungscode. Und jede Zelle kennt ihren »Nachbarn«, sie weiß, zu wem sie gehört. Ein Lebewesen ist multidimensional. Du wirst es noch herausfinden, dann, wenn du eine Ahnung davon hast, was das ist: Multidimensionalität. Ein paar deiner Kollegen, Biophysiker, wissen es schon. Du lachst über sie. Noch.
Es gibt keine glatten Kurven. Nirgendwo. Sie sind »treppenförmig«. Und wirken nur deshalb glatt, weil sie »unscharf« sind.
Es gibt nichts Unendliches! Mathematiker, merk es dir. Dann bist du gemeinsam mit den Physikern das Problem mit der Null unterhalb des Strichs los und musst keine »Ausnahmen« definieren. Lerne einfach, die alte Mathematik zu benutzen, die noch keine Null kannte. Ihre Zahlen sind sehr »natürlich«.
Sie enthalten einen »Inhalt«, der so vielfältig ist wie das gesamte Universum. Und sie sind symmetrisch. Deshalb brauchst du auch kein Komma, wenn du sie aufschreibst. Das Komma findest du immer in der Mitte. Genau auf der Nulllinie.
Die Zahlen drehen sich aus der Nulllinie heraus. Manchmal siehst du die Vorderseite des Bandes, dann wieder seine Rückseite. Aber es ist immer die gleiche Seite. Am »Wendepunkt«, dort wo das Band eine halbe Umdrehung macht und zusammengeklebt ist, wird es um 1 breiter. Zumindest scheint es so.
Das Band ist an seinem Anfang sehr schmal, dort hat es eine Breite von 1. An seinem Ende ist es so breit wie das Universum. Dort ist es dann wieder mit seinem Anfang zusammengeklebt. Und zwischendurch findest du Bänder, die mit Bändern verschlungen sind, die mit Bändern verschlungen sind. Und alle haben zwei Oberflächen, die nur eine einzige ist. Siehst du die Wendepunkte?
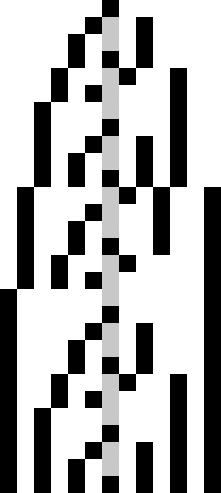
Die Zahlen laufen einmal von links nach rechts, dann wechseln sie ihre Richtung und laufen wieder zurück. Stets auf der gleichen Seite, doch dazwischen befindet sich ein Wendepunkt. Und wenn sie einmal herum sind, wenn der Kreis, der kein Ende hat, geschlossen ist, dann sind sie um genau 4 weitergewandert. Denn π = 4. In einem multidimensionalen Universum.
Einmal um die gaaanze Weeelt ... so hat Gott gesungen. Und er hatte die Taschen voller Geld.
Es ist egal, auf welcher »Ebene« sich der Zufall ausbreitet, das Wellenpaket. Er läuft einmal hin und wieder her und bleibt dabei stets in sich ausgeglichen, immer genau 1. Dennoch bildet er einen Buckel aus, einen glockenförmigen. Ein Quantum Materie. Auf der einen Seite läuft er hin, der Buckel, auf der anderen zurück. Soweit ist das Band »ganz« und bildet einen einzigen Kreis. Schneidest du es ein weiteres Mal auseinander, gebiert es eine Zwillingsschwester, von der es dennoch nicht getrennt ist.
Unsere Welt ist dual. Läufst du das Band einmal entlang, dann verdoppelt es sich und kippt. Du läufst unbeirrt weiter – dass du die Seite gewechselt hast, hast du gar nicht bemerkt – und verdoppelst es dadurch noch einmal. Es hat sich nun genau vervierfacht. Der nicht endende Kreis ist vollständig.
Die Zahlen im Dreieck verdoppeln sich mit jeder Zeile, sie wachsen um genau eine Zweierpotenz. Sowohl im Pascalschen als auch im Phi-Dreieck.
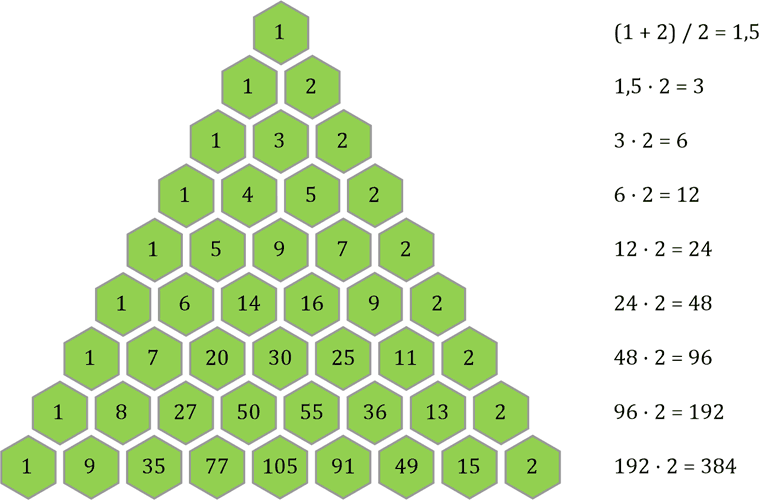
Du möchtest eine andere Dimension betreten? Drehe dich einmal vollständig um die eigene Achse. Du stehst nun zwei Schritte neben dir. Zwischen deinem alten und deinem neuen Standpunkt ist eine leere Fläche mit einer Breite von 1. Dort sitzt eine unsichtbare Katze.
Ich halte mich gerne in der Hexenküche auf. Der Weg in die Küche ist nicht weit. Ich bin von ihr nur durch einen hauchdünnen Schleier getrennt. Er hat eine Breite von h = 1. Und ich liebe Mandelbrot! Es duftet so herrlich! Es duftet nach Chaos. Nach einem streng geordneten Chaos.
Für heute mach ich Schluss. Ich komme wieder, keine Frage!
| 1 | Werner Heisenberg: Deutscher Physiker, 1901 – 1976, Nobelpreis für Physik 1932 für die Begründung der Quantenmechanik. |
| 2 | Heute wird sie auch häufig Unbestimmtheitsrelation genannt. |
| 3 | Benannt nach dem Physiker Max Planck, 1858 – 1947, der als Begründer der Quantenphysik gilt. Er erhielt für seine Entdeckung des Wirkungsquantums 1919 den Nobelpreis für Physik des Jahres 1918. |
| 4 | Sexagesimalsystem: Ein Zahlensystem mit der Basis 60. Zum Vergleich: Unser heute verwendetes Dezimalsystem hat die Basis 10. |
| 5 | Ich habe hier eine Metapher der Stimme aus dem Jenseits verwendet. Siehe Das Große Vorurteil der Wissenschaft. |
| 6 | Vergleiche Die Physik in den nächsten 500 Jahren |
| 7 | Die Stimme aus dem Jenseits hat sich dazu ziemlich ausführlich in Das interdimensionale Universum geäußert. |
Diese Seite herunterladen: PDF ODT
 |
 |
|