Cosinus Φ
Als wir die Zeilensummen im Phi-Dreieck notiert hatten, haben wir bei alternierenden Vorzeichen (abwechselnd + und −) als Ergebnis jeweils einen Wert zwischen +2 und −2 erhalten (siehe Tabelle 5 und Bild 9). Damals hatte ich gesagt, ich werde mir diese »Schlange« notieren und im Auge behalten. Zur Erinnerung hier nochmals das Bild der »Schlange«:
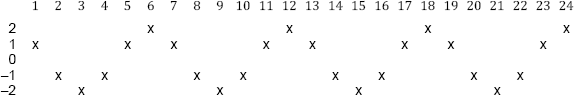
Bild 12
Die »Schlange« erinnert an die Form einer Sinus- bzw. Cosinus-Linie. Eine Sinus-Linie entsteht, wenn wir am Umfang eines Kreises »einen Punkt befestigen« und anschließend den Kreis um seinen Mittelpunkt drehen. Während wir den Kreis drehen, zeichnen wir die »Höhe« des Punktes auf, sowie auf einer horizontalen Achse den Winkel, um den wir den Kreis jeweils gedreht haben:
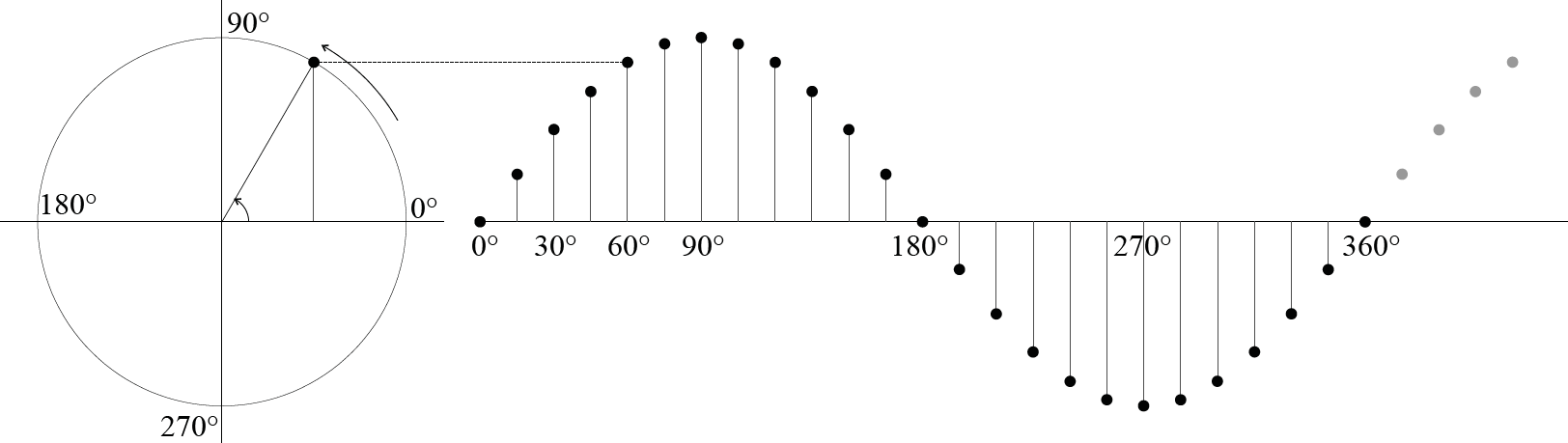
Bild 13
Die Punkte in Bild 13 liegen alle auf einer sog. »Sinus-Kurve«, welche die Grundform aller Schwingungen darstellt. Eine Cosinus-Kurve sieht genauso aus – der einzige Unterschied zur Sinus-Kurve besteht darin, dass sie dort beginnt, wo die Sinus-Kurve ihr Maximum hat. Zum Vergleich seien hier beide Kurven untereinander dargestellt:
Bild 14: Sinus
Bild 15: Cosinus
Unsere »Schlange« hat ihre Maximalwerte (obere Umkehrpunkte) bei den Potenzen 0, 6, 12, 18, 24, ... (die nullte
Potenz ist im Bild nicht eingezeichnet, da dort kein eindeutiger Wert vorhanden war). Der »logischen Fortsetzung« entlang der vertikalen
2er-Linie entspricht aber zweifellos der Wert 2. Die Schlange ist also eine Cosinus-Kurve.
In Abständen von jeweils 60° schwankt ihr »Höhen-Wert« (Techniker würden es die Amplitude nennen) rhythmisch
in einer Folge von
2 ... 1 ... −1 ... −2 ... −1 ... 1 ...

Bild 16
Eine »Standard«-Sinus- oder Cosinus-Kurve hat eine Amplitude (Maximalwert oder Scheitelwert) von genau 1. Der Kreis, welcher um seinen Mittelpunkt gedreht werden muss, um eine solche Kurve zu erzeugen, wird Einheitskreis genannt, er hat einen Radius von genau 1. Eine Sinus-Kurve ist auch dann noch eine Sinus-Kurve, wenn ihre Amplitude größer oder kleiner als 1 ist oder wenn ihre Periodenlänge kürzer oder länger ist. Wichtig ist lediglich die Form der Kurve. Will ich sie höher haben, so multipliziere ich ihre Amplitude mit einem Faktor, der größer als 1 ist. Soll sie niedriger sein, dann muss der Faktor kleiner als 1 sein. Ich kann die Kurve also beliebig dehnen und stauchen (sowohl in der Höhe als auch in der Breite), sie bleibt immer eine Sinus- oder Cosinus-Kurve.
Unsere »Schlangen«-Kurve hat eine Amplitude von genau 2. Wenn wir sie auf eine »Einheits-Cosinus-Kurve« umrechnen wollen, dann müssen wir die Amplitude in ihrem gesamten Verlauf nur durch 2 dividieren und können so überprüfen, ob die Werte an den Punkten, die uns bekannt sind, tatsächlich mit dem Amplituden-Wert einer Cosinus-Kurve an der entsprechenden Stelle übereinstimmt.
Die Periodenlänge der Schlangenkurve beträgt genau 6. Das wissen wir, weil der Abstand von einem Kurven-Maximum zum nächsten immer genau 6 ist: bei 0, 6, 12, 18, 24, ...
Da die Periodenlänge einer Sinus- oder Cosinuskurve 360° beträgt (also genau einer ganzen Umdrehung des Einheitskreises entspricht), kennen wir somit die Lage bestimmter Punkte unserer Schlangenkurve, nämlich jene im Abstand von jeweils
|
= 60° |
Wir müssen nun nur schauen, wie groß die Amplituden an diesen Stellen bei einer Standard-Cosinuskurve sind und können dann sagen, ob die Punkte genau auf der Linie liegen (bzw. darunter oder darüber).
Normale Schul-Taschenrechner haben alle Tasten, mit welcher man den Wert von »Winkelfunktionen« (Sinus, Cosinus, Tangens, ...) berechnen kann. Tippen wir also die Werte ein und rechnen nach:
| cos(0°) | = | 1 | |
| cos(60°) | = | 0 | ,5 |
| cos(120°) | = | −0 | ,5 |
| cos(180°) | = | −1 | |
| cos(240°) | = | −0 | ,5 |
| cos(300°) | = | 0 | ,5 |
| cos(360°) | = | 1 |
Da die Amplituden unserer Kurve den Wert 2 haben, müssen wir unsere Ergebnisse noch mit diesem Wert multiplizieren und erhalten somit
| 2cos(0°) | = | 2 |
| 2cos(60°) | = | 1 |
| 2cos(120°) | = | −1 |
| 2cos(180°) | = | −2 |
| 2cos(240°) | = | −1 |
| 2cos(300°) | = | 1 |
| 2cos(360°) | = | 2 |
Damit haben wir den Beweis1) erbracht, dass alle Werte unserer »Schlangenlinie« tatsächlich genau auf einer Cosinuskurve liegen!
– – –
Bevor wir uns einer anderen Herangehensweise an die Zahl Φ zuwenden, untersuchen wir die Entstehung der Schlangenlinie noch ein wenig genauer.
In der Tabelle 4 haben wir ganz links eine Spalte mit den Zahlen 1 bis 24 geschrieben und daneben den errechneten Wert der zugehörigen Potenz von Φ (auf eine ganze Zahl gerundet). Gleichzeitig entsprach das genau der Summe der Zahlen in der jeweiligen Zeile der Tabelle. Ab der Potenz 2 (und höher) funktioniert das auch problemlos, aber die Potenzen 1 und 0 von Φ bringen ein »kleines Problemchen« mit sich. Sie stimmen dort nämlich nicht mehr wirklich. Der tatsächliche Wert von Φ1 = Φ = 1,618... weicht bereits sehr weit vom Tabellenwert 1 ab und der tatsächliche Wert von Φ0 = 1 weicht vom Tabellenwert 2, der sich aus der Tabelle 27c (Lucas-Folge) ergibt, noch weiter ab. Wir sind an dieser Stelle zu dem Schluss gekommen, dass wir die Abweichungen (die mit zunehmender Höhe der Potenzen immer kleiner werden), mit Hilfe einer erweiterten Tabelle (später Sektor C genannt) lösen können. Das stimmt soweit auch.
Die Potenzreihen, die zu unserer »Schlangenlinie« geführt haben, haben wir allerdings ausschließlich mit natürlichen (ganzen) Zahlen als Basis errechnet (vergleiche Tabelle 5) – als Beispiel zur Erinnerung möge die Zeile 9 dienen:
| (Φ2)9 = Φ18 = | 5.778 = | 39 − 9⋅ | 37 + 27⋅ | 35 − 30⋅ | 33 + 9⋅ | 3 |
| (Φ3)9 = Φ27 = | 439.204 = | 49 + 9⋅ | 47 + 27⋅ | 45 + 30⋅ | 43 + 9⋅ | 4 |
| (Φ4)9 = Φ36 = | 33.385.282 = | 79 − 9⋅ | 77 + 27⋅ | 75 − 30⋅ | 73 + 9⋅ | 7 |
| (Φ5)9 = Φ45 = | 2.537.720.636 = | 119 + 9⋅ | 117 + 27⋅ | 115 + 30⋅ | 113 + 9⋅ | 11 |
| ⋮ | ||||||
Später haben wir dann auch noch die Zeile 24 mit dem Basiswert Φ1 = 1 berechnet, wobei der Wert 1 aus der Zeile 1 der Tabelle entnommen wurde. Streng genommen ist Φ1 natürlich nicht 1, sondern Φ. Ich möchte an dieser Stelle die Potenzreihe für einige Zeilen mit keinem der ganzzahligen Werte als Basis berechnen – stattdessen soll uns als Basis der Wert der tatsächlichen Zahl Φ dienen, nämlich 1,618033988...
Die Vorzeichen werde ich wie schon bei der Berechnung unserer »Schlangenlinie« alternierend verwenden, also immer abwechselnd + und −.
Das Ergebnis ist durchaus bemerkenswert:
| 1Φ0 | = | 2 (1) | ||||||||||||||||||||||||||
| 1Φ1 | = | Φ | ||||||||||||||||||||||||||
| 1Φ2 | − | 2 | Φ0 | = | Φ−1 | |||||||||||||||||||||||
| 1Φ3 | − | 3 | Φ1 | = | − | Φ−1 | ||||||||||||||||||||||
| 1Φ4 | − | 4 | Φ2 | + | 2 | Φ0 | = | − | Φ | |||||||||||||||||||
| 1Φ5 | − | 5 | Φ3 | + | 5 | Φ1 | = | − | 2 | |||||||||||||||||||
| 1Φ6 | − | 6 | Φ4 | + | 9 | Φ2 | − | 2 | Φ0 | = | − | Φ | ||||||||||||||||
| 1Φ7 | − | 7 | Φ5 | + | 14 | Φ3 | − | 7 | Φ1 | = | − | Φ−1 | ||||||||||||||||
| 1Φ8 | − | 8 | Φ6 | + | 20 | Φ4 | − | 16 | Φ2 | + | 2 | Φ0 | = | Φ−1 | ||||||||||||||
| 1Φ9 | − | 9 | Φ7 | + | 27 | Φ5 | − | 30 | Φ3 | + | 9 | Φ1 | = | Φ | ||||||||||||||
| 1Φ10 | − | 10 | Φ8 | + | 35 | Φ6 | − | 50 | Φ4 | + | 25 | Φ2 | − | 2 | Φ0 | = | 2 | |||||||||||
| 1Φ11 | − | 11 | Φ9 | + | 44 | Φ7 | − | 77 | Φ5 | + | 55 | Φ3 | − | 11 | Φ1 | = | Φ | |||||||||||
| 1Φ12 | − | 12 | Φ10 | + | 54 | Φ8 | − | 112 | Φ6 | + | 105 | Φ4 | − | 36 | Φ2 | + | 2Φ0 | = | Φ−1 | |||||||||
| 1Φ13 | − | 13 | Φ11 | + | 65 | Φ9 | − | 156 | Φ7 | + | 182 | Φ5 | − | 91 | Φ3 | + | 13Φ1 | = | − | Φ−1 | ||||||||
| 1Φ14 | − | 14 | Φ12 | + | 77 | Φ10 | − | 210 | Φ8 | + | 294 | Φ6 | − | 196 | Φ4 | + | 49Φ2 | − | 2Φ0 | = | − | Φ | ||||||
| 1Φ15 | − | 15 | Φ13 | + | 90 | Φ11 | − | 275 | Φ9 | + | 450 | Φ7 | − | 378 | Φ5 | + | 140Φ3 | − | 15Φ1 | = | − | 2 | ||||||
| 1Φ16 | − | 16 | Φ14 | + | 104 | Φ12 | − | 352 | Φ10 | + | 660 | Φ8 | − | 672 | Φ6 | + | 336Φ4 | − | 64Φ2 | + | 2Φ0 | = | − | Φ | ||||
| 1Φ17 | − | 17 | Φ15 | + | 119 | Φ13 | − | 442 | Φ11 | + | 935 | Φ9 | − | 1122 | Φ7 | + | 714Φ5 | − | 204Φ3 | + | 17Φ1 | = | − | Φ−1 | ||||
| 1Φ18 | − | 18 | Φ16 | + | 135 | Φ14 | − | 546 | Φ12 | + | 1287 | Φ10 | − | 1782 | Φ8 | + | 1386Φ6 | − | 540Φ4 | + | 81Φ2 | − | 2Φ0 | = | Φ−1 | |||
| 1Φ19 | − | 19 | Φ17 | + | 152 | Φ15 | − | 665 | Φ13 | + | 1729 | Φ11 | − | 2717 | Φ9 | + | 2508Φ7 | − | 1254Φ5 | + | 285Φ3 | − | 19Φ1 | = | Φ | |||
| 1Φ20 | − | 20 | Φ18 | + | 170 | Φ16 | − | 800 | Φ14 | + | 2275 | Φ12 | − | 4004 | Φ10 | + | 4290Φ8 | − | 2640Φ6 | + | 825Φ4 | − | 100Φ2 | + | 2Φ0 | = | 2 | |
| 1Φ21 | − | 21 | Φ19 | + | 189 | Φ17 | − | 952 | Φ15 | + | 2940 | Φ13 | − | 5733 | Φ11 | + | 7007Φ9 | − | 5148Φ7 | + | 2079Φ5 | − | 385Φ3 | + | 21Φ1 | = | Φ | |

Bild 17
Die Cosinuskurve (ich nenne sie jetzt nicht mehr »Schlangenlinie«) ist wieder sichtbar! Mit gleicher Amplitude, allerdings anderer Periodenlänge! Die Periodenlänge (Abstand zwischen zwei Maximalwerten) beträgt nun nicht mehr 6 sondern 10. Und auch die Punkte liegen wie vorhin exakt auf der Cosinuskurve! Wir überprüfen das:
Zunächst stellen wir fest, dass die einzelnen Punkte in horizontaler Richtung (hier sind die Winkelgrade auf dem Einheitskreis aufgetragen) je 36° Abstand zueinander aufweisen.
|
= 36° |
Tippen wir die Grad-Werte an diesen Stellen in den Taschenrechner ein, erhalten wir folgende Ergebnisse:
| cos(0°) | = | 1 | ||||||||||||||||
| cos(36°) | = | 0 | ,809016994 | = |
|
= |
|
|||||||||||
| cos(72°) | = | 0 | ,309016994 | = |
|
= |
|
= |
|
|||||||||
| cos(108°) | = | −0 | ,309016994 | = |
|
= |
|
= − |
|
|||||||||
| cos(144°) | = | −0 | ,809016994 | = |
|
= − |
|
|||||||||||
| cos(180°) | = | −1 | ||||||||||||||||
| cos(216°) | = | −0 | ,809016994 | = |
|
= − |
|
|||||||||||
| cos(252°) | = | −0 | ,309016994 | = |
|
= |
|
= − |
|
|||||||||
| cos(288°) | = | 0 | ,309016994 | = |
|
= |
|
= |
|
|||||||||
| cos(324°) | = | 0 | ,809016994 | = |
|
= |
|
|||||||||||
| cos(360°) | = | 1 |
Da die Amplitude wiederum 2 ist, müssen wir die Gleichungen auch noch auf beiden Seiten mit 2 multiplizieren
| 2cos(0°) | = | 2 |
| 2cos(36°) | = | Φ |
| 2cos(72°) | = | Φ−1 |
| 2cos(108°) | = − | Φ−1 |
| 2cos(144°) | = − | Φ |
| 2cos(180°) | = − | 2 |
| 2cos(216°) | = − | Φ |
| 2cos(252°) | = − | Φ−1 |
| 2cos(288°) | = | Φ−1 |
| 2cos(324°) | = | Φ |
| 2cos(360°) | = | 2 |
und erhalten die Bestätigung, dass sämtliche Punkte genau auf der Kurve liegen.
Die Ergebnisse der Potenzreihen mit der Basiszahl Φ habe ich vorhin einfach hingeschrieben. Wir sollten das noch überprüfen und können das leicht mit Hilfe unserer Berechnungsmethode für die Potenzen von Φ machen:
Ich beginne in der allerersten Zeile (mit der Potenz 0) jedoch gleich mit einem mathematischen Nonsens:
Φ0 = 1 = 2
Eine Zahl kann unmöglich gleichzeitig zwei verschiedene Werte haben! Diesen Widerspruch haben wir bereits bei den Tabellen 27b und 27c gesehen. Φ0 = 1 entspricht dem »richtig gerechneten« Ergebnis. Die Cosinuskurve jedoch meint dazu etwas ganz anderes. Es wäre ein ebensolcher Nonsens, die Kurve ab 36° bis in alle Ewigkeit mit einem Maximalwert von 2 fortlaufen zu lassen, beim Winkel 0° sollte sie jedoch plötzlich einen Wert von 1 haben ... Haben wir irgendwo einen kapitalen Fehler gemacht? Vielleicht. Vielleicht auch nicht.
Fahren wir fort, die Zeilen mit den Potenzen 1 bis 21 zu berechnen:
Φ1 = Φ
Φ2 − 2Φ0 = Φ−1
1(1Φ + 1) − 2(0Φ + 1) =
1Φ + 1 − 0Φ − 2 = 1Φ − 1 = Φ−1
Φ3 − 3Φ1 = −Φ−1
1(2Φ + 1) − 3(1Φ + 0) =
2Φ + 1 − 3Φ − 0 = −1Φ + 1 = −Φ−1
Φ4 − 4Φ2 + 2Φ0 = −Φ
1(3Φ + 2) − 4(1Φ + 1) + 2(0Φ + 1) =
3Φ + 2 − 4Φ − 4 + 0Φ + 2 = −1Φ + 0 = −Φ
Φ5 − 5Φ3 + 5Φ1 = −2
1(5Φ + 3) − 5(2Φ + 1) + 5(1Φ + 0) =
5Φ + 3 − 10Φ − 5 + 5Φ + 0 = 0Φ − 2 = −2
Φ6 − 6Φ4 + 9Φ2 − 2Φ0 = −Φ
1(8Φ + 5) − 6(3Φ + 2) + 9(Φ + 1) − 2(0Φ + 1) =
8Φ + 5 − 18Φ − 12 + 9Φ + 9 − 2 = −Φ
Φ7 − 7Φ5 + 14Φ3 − 7Φ1 = −Φ−1
1(13Φ + 8) − 7(5Φ + 3) + 14(2Φ + 1) − 7(1Φ + 0) =
13Φ + 8 − 35Φ − 21 + 28Φ + 14 − 7Φ − 0 = −1Φ + 1 = −Φ−1
Φ8 − 8Φ6 + 20Φ4 − 16Φ2 + 2Φ0 = Φ−1
1(21Φ + 13) − 8(8Φ + 5) + 20(3Φ + 2) − 16(Φ + 1) + 2(0Φ + 1) =
21Φ + 13 − 64Φ − 40 + 60Φ + 40 − 16Φ − 16 + 0Φ + 2 = 1Φ − 1 = Φ−1
Φ9 − 9Φ7 + 27Φ5 − 30Φ3 + 9Φ1 = Φ
1(34Φ + 21) − 9(13Φ + 8) + 27(5Φ + 3) − 30(2Φ + 1) + 9(1Φ + 0) =
34Φ + 21 − 117Φ − 72 + 135Φ + 81 − 60Φ − 30 + 9Φ + 0 = 1Φ ± 0 = Φ
Φ10 − 10Φ8 + 35Φ6 − 50Φ4 + 25Φ2 − 2Φ0 = 2
1(55Φ + 34) − 10(21Φ + 13) + 35(8Φ + 5) − 50(3Φ + 2) + 25(1Φ + 1) − 2(0Φ + 1) =
55Φ + 34 − 210Φ − 130 + 280Φ + 175 − 150Φ − 100 + 25Φ + 25 − 0Φ − 2 = ±0Φ + 2 = 2
Φ11 − 11Φ9 + 44Φ7 − 77Φ5 + 55Φ3 − 11Φ1 = Φ
1(89Φ + 55) − 11(34Φ + 21) + 44(13Φ + 8) − 77(5Φ + 3) + 55(2Φ + 1) − 11(1Φ + 0) =
89Φ + 55 − 374Φ − 231 + 572Φ + 352 − 385Φ − 231 + 110Φ + 55 − 11Φ − 0 = 1Φ ± 0 = Φ
Φ12 − 12Φ10 + 54Φ8 − 112Φ6 + 105Φ4 − 36Φ2 + 2Φ0 = Φ−1
1(144Φ + 89) − 12(55Φ + 34) + 54(21Φ + 13) − 112(8Φ + 5) + 105(3Φ + 2) − 36(1Φ + 1) + 2(0Φ + 1) =
144Φ + 89 − 660Φ − 408 + 1.134Φ + 702 − 896Φ − 560 + 315Φ + 210 − 36Φ − 36 + 0Φ + 2 = −1Φ − 1 = Φ−1
Φ13 − 13Φ11 + 65Φ9 − 156Φ7 + 182Φ5 − 91Φ3 + 13Φ1 = −Φ−1
1(233Φ + 144) − 13(89Φ + 55) + 65(34Φ + 21) − 156(13Φ + 8) + 182(5Φ + 3) − 91(2Φ + 1) + 13(1Φ + 0) =
233Φ + 144 − 1.157Φ − 715 + 2.110Φ + 1.365 − 2.028Φ − 1.248 + 910Φ + 546 − 182Φ − 91 + 13Φ + 0 = −1Φ + 1 = −Φ−1
Φ14 − 14Φ12 + 77Φ10 − 210Φ8 + 294Φ6 − 196Φ4 + 49Φ2 − 2Φ0 = −Φ
1(377Φ + 233) − 14(144Φ + 89) + 77(55Φ + 34) − 210(21Φ + 13) + 294(8Φ + 5) − 196(3Φ + 2) + 49(1Φ + 1) − 2(0Φ + 1) =
377Φ + 233 − 2.016Φ − 1.246 + 4.235Φ + 2.618 − 4.410Φ − 2.730 + 2.352Φ + 1.470 − 588Φ − 392 + 49Φ + 49 − 0Φ − 2 = −1Φ ± 0 = −Φ
Φ15 − 15Φ13 + 90Φ11 − 275Φ9 + 450Φ7 − 378Φ5 + 140Φ3 − 15Φ1 = −2
1(610Φ + 377) − 15(233Φ + 144) + 90(89Φ + 55) − 275(34Φ + 21) + 450(13Φ + 8) − 378(5Φ + 3) + 140(2Φ + 1) − 15Φ1 =
610Φ + 377 − 3.495Φ − 2.160 + 8.010Φ + 4.950 − 9.350Φ − 5.775 + 5.850Φ + 3.600 − 1.890Φ − 1.134 + 280Φ + 140 − 15Φ = −2
Φ16 − 16Φ14 + 104Φ12 − 352Φ10 + 660Φ8 − 672Φ6 + 336Φ4 − 64Φ2 + 2Φ0 = −Φ
1(987Φ + 610) − 16(377Φ + 233) + 104(144Φ + 89) − 352(55Φ + 34) + 660(21Φ + 13) − 672(8Φ + 5) + 336(3Φ + 2) − 64(Φ + 1) + 2(0Φ + 1) =
987Φ + 610 − 6.032Φ − 3.728 + 14.976Φ + 9.256 − 19.360Φ − 11.968 + 13.860Φ + 8.580 − 5.376Φ − 3.360 + 1.008Φ + 672 − 64Φ − 64 + 0Φ + 2 =
−1Φ ± 0 = −Φ
Φ17 − 17Φ15 + 119Φ13 − 442Φ11 + 935Φ9 − 1.122Φ7 + 714Φ5 − 204Φ3 + 17Φ1 = −Φ−1
1(1.597Φ + 987) − 17(610Φ + 377) + 119(233Φ + 144) − 442(89Φ + 55) + 935(34Φ + 21) − 1.122(13Φ + 8) + 714(5Φ + 3) − 204(2Φ + 1) + 17(1Φ + 0) =
1.597Φ + 987 − 10.370Φ − 6.409 + 27.727Φ + 17.136 − 39.338Φ − 24.310 + 31.790Φ + 19.635 − 14.586Φ − 8.976 + 3.570Φ + 2.142 − 408Φ − 204 + 17Φ + 0 =
−1Φ + 1 = −Φ−1
Φ18 − 18Φ16 + 135Φ14 − 546Φ12 + 1.287Φ10 − 1.782Φ8 + 1.386Φ6 − 540Φ4 + 81Φ2 − 2Φ0 = Φ−1
1(2.584Φ + 1.597) − 18(987Φ + 610) + 135(377Φ + 233) − 546(144Φ + 89) + 1.287(55Φ + 34) − 1.782(21Φ + 13) + 1.386(8Φ + 5) − 540(3Φ + 2) + 81(Φ + 1) − 2(0Φ + 1) =
2.584Φ + 1.597 − 17.766Φ − 10.980 + 50.895Φ + 31.455 − 78.624Φ − 48.594 + 70.785Φ + 43.758 − 37.422Φ − 23.166 + 11.088Φ + 6.930 − 1.620Φ − 1.080 + 81Φ + 81 − 0Φ − 2 =
1Φ − 1 = Φ−1
Φ19 − 19Φ17 + 152Φ15 − 665Φ13 + 1.729Φ11 − 2.717Φ9 + 2.508Φ7 − 1.254Φ5 + 285Φ3 − 19Φ1 = Φ
1(4.181Φ + 2.584) − 19(1.597Φ + 987) + 152(610Φ + 377) − 665(233Φ + 144) + 1.729(89Φ + 55) − 2.717(34Φ + 21) + 2.508(13Φ + 8) − 1.254(5Φ + 3) + 285(2Φ + 1) − 19(1Φ + 0) =
4.181Φ + 2.584 − 30.343Φ − 18.753 + 92.720Φ + 57.304 − 154.945Φ − 95.760 + 153.881Φ + 95.095 − 92.378Φ − 57.057 + 32.604Φ + 20.064 − 6.270Φ − 3.762 + 570Φ + 285 − 19Φ − 0 =
1Φ ± 0 = Φ
Φ20 − 20Φ18 + 170Φ16 − 800Φ14 + 2.275Φ12 − 4.004Φ10 + 4.290Φ8 − 2.640Φ6 + 825Φ4 − 100Φ2 + 2Φ0 = 2
1(6.765Φ + 4.181) − 20(2.584Φ + 1.597) + 170(987Φ + 610) − 800(377Φ + 233) + 2.275(144Φ + 89) − 4.004(55Φ + 34) + 4.290(21Φ + 13) − 2.640(8Φ + 5) + 825(3Φ + 2) − 100(1Φ + 1) + 2(0Φ + 1) =
6.765Φ + 4.181 − 51.680Φ − 31.940 + 167.790Φ + 103.700 − 301.600Φ − 186.400 + 327.600Φ + 202.475 − 220.220Φ − 136.136 + 90.090Φ + 55.770 − 21.120Φ − 13.200 + 2.475Φ + 1.650 − 100Φ − 100 + 0Φ + 2 =
±0Φ + 2 = 2
Φ21 − 21Φ19 + 189Φ17 − 952Φ15 + 2.940Φ13 − 5.733Φ11 + 7.007Φ9 − 5.148Φ7 + 2.079Φ5 − 385Φ3 + 21Φ1 = Φ
1(10.946Φ + 6.765) − 21(4.181Φ + 2.584) + 189(1.597Φ + 987) − 952(610Φ + 377) + 2.940(233Φ + 144) − 5.733(89Φ + 55) + 7.007(34Φ + 21) − 5.148(13Φ + 8) + 2.079(5Φ + 3) − 385(2Φ + 1) + 21(1Φ + 0) =
10.946Φ + 6.765 − 87.801Φ − 54.264 + 301.833Φ + 186.543 − 580.720Φ − 358.904 + 685.020Φ + 423.360 − 510.237Φ − 315.315 + 238.238Φ + 147.147 − 66.924Φ − 41.184 + 10.395Φ + 6.237 − 770Φ − 385 + 21Φ + 0 =
1Φ ± 0 = Φ
Ab der Zeile 1 ergab unsere Überprüfung: Fehlerfrei!
– – –
Wie bereits angekündigt machen wir nun einen Abstecher zu etwas ganz Anderem – aber versprochen: Wir landen am Ende des Kapitels garantiert wieder bei unserer Zahl Φ!
| 1 | Im mathematischen Sinne ist es natürlich kein »Beweis«, wenn man auf einem Taschenrechner übereinstimmende Ergebnisse erhält. Dieses Buch stellt aber ganz bewusst einfachere Anforderungen und so möge uns dieser »Beweis« genügen. Mathematiker und Ingenieure wissen ohnehin, dass das Ergebnis tatsächlich richtig ist. |
