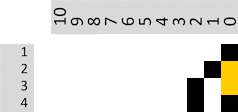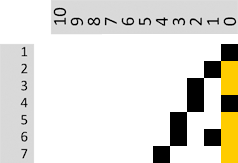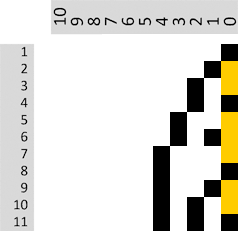Zahlensysteme
Wir benutzen zum Rechnen Zahlen, die sich aus Ziffern zusammensetzen. In unserer heutigen Welt wird allgemein das sog. Dezimalsystem für die Darstellung von Zahlen verwendet. Dezi leitet sich vom lateinischen decem ab und bedeutet zehn. Das Dezimalsystem verwendet zehn verschiedene Ziffern von 0 bis 9.
Es sind heute auch noch andere Zahlensysteme in Verwendung, auch wenn wir sie im Alltag kaum bemerken. Alle unsere Computer verwenden z. B. das Dualsystem, das nur 2 verschiedene Ziffern braucht, um alle Zahlen darstellen zu können. Diese beiden Ziffern sind 0 und 1. Davon abgeleitet wird in Computern auch noch das Oktalsystem (mit 8 verschiedenen Ziffern) sowie das Hexadezimalsystem (mit 16 verschiedenen Ziffern) verwendet.
Das Wesentliche eines Zahlensystems ist dessen Basis. Die Basis gibt an, wieviele verschiedene Ziffern für die Darstellung von Zahlen verwendet werden. Beim erwähnten Dezimalsystem ist die Basis 10. Die Darstellung von Zahlen, die größer als die größte Ziffer 9 sind, erfolgt in einem Stellenwertsystem. Dieses lässt sich anhand eines Beispiels gut erklären.
Wenn ich eine größere Zahl aufschreiben will, nehmen wir die Zahl 24.753, dann hat deren Ziffernfolge 2-4-7-5-3 eine bestimmte Bedeutung (der Punkt zwischen 24 und 753 dient nur zur »Orientierung«, er kann auch weggelassen werden).
| 24753 | = | 2⋅104 | + 4⋅103 | + 7⋅102 | + 5⋅101 | + 3⋅100 |
| = | 2⋅10000 | + 4⋅1000 | + 7⋅100 | + 5⋅10 | + 3⋅1 | |
| = | 20000 | + 4000 | + 700 | + 50 | + 3 |
Die Stellen, an welchen die Ziffern stehen, geben also an, mit welcher Potenz der Basis 10 ich die Ziffer an dieser Stelle multiplizieren muss. Die ganz rechte Stelle ist die Stelle 0, dann folgen links davon die Stellen 1, 2, 3, ... usw.
Etwas anders ausgedrückt: Die einzelne Ziffer muss so oft, wie es ihrer Stelle entspricht, mit der Basiszahl multipliziert werden. Die Ziffer 2 steht an der Stelle 4, ich muss sie daher mit 10000 multiplizieren, bzw. ich muss »4 Nullen dranhängen«. Die Ziffer 3 steht an der Stelle 0, ich muss sie daher gar nicht mit der Basiszahl multiplizieren.
Mit diesem System, wie wir es bisher besprochen haben, kann ich jedoch nur ganze Zahlen darstellen. Wie stelle ich eine Zahl dar, die eine Größe zwischen den ganzen Zahlen hat? Nun, es ist uns gut bekannt: Wir verwenden dafür das Komma. Es hat keine andere Funktion als die Position der Stelle 0 anzuzeigen. Unmittelbar links vom Komma befindet sich die Stelle 0, rechts davon bekommen die Potenzen, mit denen die dort hingeschriebenen Ziffern zu multiplizieren sind, negative Werte.
Als Beispiel nehmen wir diesmal die Zahl 37,125. Wir können das Ergebnis einer Division »297 geteilt durch 8« als Bruch hinschreiben
| 297 |
| 8 |
oder auch in der Dezimalschreibweise als 37,125.
| 37,125 | = | 3⋅101 | + 7⋅100 | + 1⋅10−1 | + 2⋅10−2 | + 5⋅10−3 |
| = | 3⋅10 | + 7⋅1 | + 1⋅0,1 | + 2⋅0,01 | + 5⋅0,001 | |
| = | 30 | + 7 | + 0,1 | + 0,02 | + 0,005 |
Mit dieser Methode können wir jede Zahl darstellen – allerdings mit einer gewissen Einschränkung, denn manche Zahlen lassen sich auf diese Weise nicht exakt darstellen. Der Bruch
| 1 |
| 7 |
kann in der Dezimalschreibweise nicht beliebig genau dargestellt werden, da das Ergebnis eine unendliche Menge an Ziffern rechts vom Komma erfordert:
|
= 0,142857142857142857142857... |
Im Fall von 1 geteilt durch 7 können wir uns noch helfen, da sich die Ziffernfolge rechts vom Komma nach jeweils 6 Ziffern wiederholt: 142857 142857 142857 142857 ...
Wir können deren sog. Periode mit einem Querstrich oberhalb der sich wiederholenden Ziffern markieren
|
= 0,142857 |
und erhalten so eine relativ kurze und dennoch eindeutige Schreibweise für die Dezimalzahl.
Es gibt jedoch viele Zahlen, bei denen diese Methode nicht funktioniert, da ihre Dezimalschreibweise unendlich viele Ziffern nach dem Komma erfordert, die nicht periodisch sind. Beispiele dafür sind
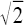
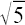
Die Zahl π (gesprochen: Pi) wurde am 11. November 2016 von einem Computer auf mehr als 22 Billionen Stellen nach dem Komma genau berechnet. Ob das Ergebnis tatsächlich richtig war, habe ich allerdings nicht überprüft ...
Alle bekannten Zahlensysteme verwenden als Basis eine natürliche Zahl, also eine positive ganze Zahl. Wir kennen Systeme mit den Basiszahlen 2, 8, 10, 12, 16, 20 (dieses wurde z. B. vom Volk der Maya verwendet) oder auch 64 – es gibt noch eine Menge mehr darüber zu erzählen.
Ich habe mir nun die Frage gestellt, ob man nicht auch ein Zahlensystem schaffen könnte, dessen Basis eine nicht-ganzzahlige Zahl ist. Wie wäre es mit einem System, dessen Basis 4,37 ist? Grundsätzlich spricht nichts dagegen, denn man kann tatsächlich mit jeder beliebigen Zahl ein solches System »zusammenbauen«. Probieren wir das anhand eines Beispiels aus:
Ich möchte die Zahl 561,42 in einem System mit der Basis 4,37 darstellen. Bittet man einen Mathematiker darum, das zu beschreiben, dann kommt garantiert das Wort »Logarithmus« darin vor. Das Logarithmieren ist die »Umkehroperation des Potenzierens«. Aber da dieser Text nicht für Mathematiker geschrieben ist, will ich die Erklärung eines Logarithmus hier vermeiden und verwende deshalb eine »einfachere« Beschreibung.
Die erste grundsätzliche Frage, die es zu klären gilt, ist: Welche Ziffern verwende ich für mein Zahlensystem? Im Dezimalsystem verwenden wir bekanntlich die Ziffern 0, 1, 2, 3, 4, 5, 6, 7, 8 und 9. In einem Oktalsystem werden die Ziffern 0, 1, 2, 3, 4, 5, 6 und 7 verwendet, im Dualsystem die Ziffern 0 und 1. Ich könnte also sinngemäß für mein spezielles System mit der Basis 4,37 die Ziffern 0, 1, 2 und 3 verwenden. Allerdings kratze ich mich nach kurzer Zeit am Kopf, wenn ich das umsetzen will, denn mir fehlt noch eine restliche Ziffer »3,37«, ... Diese könnte ich mir künstlich erschaffen, indem ich sie einfach mit einem beliebigen anderen Zeichen, z. B. dem Buchstaben K, benenne. Dadurch ergibt sich aber ein weiteres Problem, und zwar ein ziemlich unangenehmes: Der »Abstand« zwischen den einzelnen Ziffern ist nicht mehr gleich groß. In allen bekannten Systemen ist dieser Abstand nämlich immer genau 1:
1 = 0 + 1
2 = 1 + 1
3 = 2 + 1
4 = 3 + 1
⋮
In unserem System wäre der Abstand zwischen der vorletzten Ziffer 3 und der letzten Ziffer K nur 0,37, während er zwischen allen anderen Ziffern jeweils 1 wäre. Das ist »unschön«. Ich sollte also eventuell den Wert der Ziffern so wählen, dass er jeweils gleich groß ist. Aber auch das ist alles andere als »schön«, da ich auf diese Weise keine »ganzen« Zahlen mehr darstellen kann. Wenn ich 4,37 auf 5 verschiedene Ziffern A, B, C, D und E so aufteile, dass deren Abstand zueinander gleich groß ist, ergibt das einen »Abstand« (in Dezimalschreibweise) von
|
= 0,874 |
Die einzelnen Ziffern hätten also einen Dezimalwert von
| A | = | 0 |
| B | = | 0,874 |
| C | = | 1,748 |
| D | = | 2,622 |
| E | = | 3,496 |
Ich beschreibe nun ein kurzes Gedankenexperiment, um die Verwendung der Ziffern A bis E zu demonstrieren. Ich nehme an, dass direkt vor mir kein Hund steht. Dann kann ich auch sagen, vor mir stehen A Hunde, denn A hat den Wert 0. Stehen vor mir allerdings ein oder zwei Hunde, dann wird es lustig, wenn ich das mit meinem »schrägen« Zahlensystem ausdrücken will ... Denn es klingt ziemlich »schräg«, wenn ich sage: »Vor mir stehen B komma ACDB Hunde«, was aber tatsächlich im Zahlensystem 4,37 der korrekten Aussage entspräche, dass ein Hund vor mir steht.
Wir sehen, unsere »natürlichen Zahlen« – also die ganzen Zahlen 0, 1, 2, 3, 4, ... – sind nicht zufällig so benannt.
Zum Abschluss dieser Erläuterung sei noch erwähnt, dass ich für unser »schräges« Zahlensystem 5 Ziffern verwendet habe. Genausogut hätte ich 7 oder 13 verschiedene Ziffern verwenden können – ich hätte immer das Problem gehabt, damit keine »natürlichen Zahlen« auf brauchbare Weise ausdrücken zu können. Was ich definitiv nicht kann, ist 4,37 verschiedene Ziffern zu verwenden. Eine Ziffer ist nun mal so etwas wie ein konkreter »Gegenstand«, selbst wenn dieser nur in unseren Gedanken existiert. Eine Anzahl konkreter Dinge verlangt zwingend eine »natürliche Zahl«, um sie abzählen zu können. So etwas wie 3,81 Katzen kann es im Konkreten, in unserer »realen« Welt, nicht geben.
Kehren wir zurück zu unserem »schrägen« Zahlensystem. Ich hatte vorhin vorgeschlagen, für dieses System 5 verschiedene Ziffern zu verwenden. Es mussten mindestens 5 Ziffern sein, weil ich bei Verwendung von weniger als 5, also z. B. nur 4 Ziffern, nicht mehr alle natürlichen Zahlen darstellen könnte. Der »Abstand« zwischen zwei Ziffern darf nicht größer als 1 sein, da sonst »Lücken« im Zahlensystem entstehen würden. Bei Verwendung von nur 4 Ziffern wäre der Abstand zwischen den einzelnen Ziffern
|
= 1,0925 |
und damit größer als 1. Die 4 Ziffern – nennen wir sie A, B, C und D – hätten folglich die Dezimalwerte
| A | = | 0 |
| B | = | 1,0925 |
| C | = | 2,185 |
| D | = | 3,2775 |
Die Potenzen unserer Basis 4,37 wären (in Dezimalziffern)
| ⋮ | |||
| 4,37−4 | = | 0 | ,00274204... |
| 4,37−3 | = | 0 | ,01198273... |
| 4,37−2 | = | 0 | ,05236452... |
| 4,37−1 | = | 0 | ,22883295... |
| 4,370 | = | 1 | |
| 4,371 | = | 4 | ,37 |
| 4,372 | = | 19 | ,0969 |
| 4,373 | = | 83 | ,453453 |
| ⋮ |
Ein Beispiel: Die (Dezimal-)Zahl 12, mit unseren 4 Ziffern geschrieben, lautet:
CC,BABB...
Wie habe ich das umgerechnet? Ich habe damit begonnen, die höchste Stelle in meinem System zu suchen, das ist in unserem Fall die 2. Stelle links vom Komma. Dort stehen die Ziffern, die mit der 1. Potenz der Basis multipliziert werden müssen. Eine weitere Stelle links vom Komma (an der 3. Stelle) stehen die Ziffern, die mit der 2. Potenz multipliziert werden müssen, das wäre in unserem Fall 4,372 = 19,0969, eine Zahl, die bereits größer als die gesuchte Zahl 12 ist. An der 2. Stelle muss also eine Ziffer stehen, die mit der 1. Potenz der Basis multipliziert einen kleineren Betrag als 12 liefert. – Konkret: Ich probiere aus
D⋅4,371 = 3,2775⋅4,37 = 14,322675
Das ist größer als 12, also nehme ich die nächstkleinere Ziffer C:
C⋅4,371 = 2,185⋅4,37 = 9,54845
Das passt. An der 2. Stelle steht also die Ziffer C. Zur Zahl 12 fehlt jetzt noch die Differenz 12 − 9,54845 = 2,45155. Welche Ziffer kommt nun an die 1. Stelle links vom Komma? Dort stehen die Ziffern, die mit der nullten Potenz der Basis multipliziert werden müssen – also mit 1. Die Ziffer D = 3,2775 ist wieder zu groß, die Ziffer C = 2,185 ist kleiner, wir schreiben also C an die 1. Stelle links vom Komma. Unsere Zahl lautet nun CC. Sie ist aber noch ziemlich ungenau, also berechnen wir auch noch ein paar Stellen rechts vom Komma, bis wir ein ausreichend genaues Ergebnis erhalten. Bisher haben wir
CC = 2,185⋅4,37 + 2,185⋅1 = 9,54845 + 2,185 = 11,73345
Es fehlen also noch 12 − 11,73345 = 0,26655. An der Stelle rechts vom Komma stehen die Ziffern, die mit der −1. Potenz (»minus ersten Potenz«) der Basis multipliziert werden müssen, also mit 4,37–1. Ich wähle die Ziffer B, denn B = 1,0925 und somit 4,37−1 = 1,0925⋅0,22883295 = 0,25. Das ist nur wenig kleiner als 0,26655 und ist somit die richtige Ziffer für diese Stelle. Unser Ergebnis ist nun also bereits auf 1 Stelle nach dem Komma genau: CC,B
Es fehlen uns jetzt auf die Zahl 12 nur noch 0,26655 − 0,25 = 0,01655. Gibt es an der 2. Stelle rechts vom Komma eine Ziffer, deren Wert kleiner als 0,01655 ist? Nein. Also schreiben wir an dieser Stelle die Ziffer A (die den Wert 0 hat) hin. An der 3. Stelle rechts vom Komma gibt es dann eine Ziffer, die kleiner als 0,01655 ist, nämlich 4,37–3 = 1,0925⋅0,01198273 = 0,013091133. Unsere gesuchte Zahl ist nun auf bereits 3 Stellen nach dem Komma genau: CC,BAB
Die Differenz zu 12 beträgt jetzt nur noch 12 − 0,013091133 = 0,003458867. An der 4. Stelle nach dem Komma kommt also wieder die Ziffer B, denn 4,37−4 = 1,0925⋅0,00274204 = 0,00299568. Die Differenz zu 12 schrumpft weiter auf 0,003458867 − 0,00299568 = 0,000463187. Unser Ergebnis lautet jetzt bereits recht genau CC,BABB.
Da wir nun die Methode des Umrechnens kennen, können wir uns ein weiteres Beispiel anschauen – nehmen wir die (Dezimal-)Zahl 18,8.
Die höchste Stelle ist die 2. Stelle links vom Komma, da 18,8 kleiner als 4,372 = 19,0969 ist. Es kommt dort die Ziffer D hin, es bleibt der Rest
18,8 − D⋅4,371 = 18,8 − 3,2775⋅4,37 = 18,8 − 14,322675 = 4,477325
Dieser Rest ist nun aber größer als die Basiszahl 4,37 und ich habe keine Möglichkeit, die »Lücke« zwischen dem Rest 4,477325 und der Basis 4,37 mit Ziffern rechts von der 2. Stelle aufzufüllen. Der Grund für das Entstehen einer Lücke ist die Tatsache, dass der »Abstand« zwischen den Ziffern A, B, C und D jeweils größer als 1 ist. Eine Darstellung aller Zahlen funktioniert nur, wenn der Abstand zwischen den Ziffern kleiner oder höchstens gleich 1 ist.
Das einfachste Zahlensystem, das wir kennen, ist das Dualsystem, das nur die beiden Ziffern 0 und 1 verwendet und mit dem unsere Computer rechnen. Diese können deshalb so schnell rechnen, weil das Rechnen durch extrem schnell aufeinander folgende Ein- und Ausschaltvorgänge von winzigen elektronischen Schaltern geschieht. 1 bedeutet »eingeschaltet«, 0 bedeutet »ausgeschaltet«. Die meisten der heute verwendeten Rechner führen etwa 2 bis 4 Milliarden Schaltvorgänge pro Sekunde aus. Und da in den Prozessoren meistens 64 Stellen gleichzeitig (parallel) berechnet werden, erhöht das die Rechengeschwindigkeit nochmals beträchtlich.
Das Dualsystem hat den Vorteil, dass auch »komplizierte« Berechnungen wie eine Multiplikation durch einfaches »Verschieben« von Zahlen und anschließender Addition durchgeführt werden können. Für eine Addition von zwei Dualziffern brauche ich nur 4 mögliche »Zustände« zu berücksichtigen: 0 + 0 = 0, 0 + 1 = 1, 1 + 0 = 1 und 1 + 1 = 0 mit einem Übertrag von 1. So etwas Einfaches lässt sich in einem Computer-Chip »fest verdrahten« und damit extrem schnell berechnen.
Wir haben beim Dualsystem gesehen, dass wir dort im Grunde gar keine Ziffern mehr benötigt haben. Denn die Ziffern 0 und 1 könnte man genausogut als ja und nein oder ein und aus bezeichnen. Wichtig in diesem System war nur, ob an einer bestimmten Stelle im Stellenwertsystem eine 1 (oder ja oder ein) vorhanden war. An diesen Stellen stand dann die jeweilige Potenz der Basis 2. Bei einer 0 (oder nein oder aus) stand dort nichts bzw. eine 0.
Wird die Basis kleiner als 2, funktioniert dieses Prinzip immer noch. Wir können unsere Ziffern 0 und 1 beibehalten – die 1 bedeutet dann nichts Anderes, als dass an dieser Stelle die jeweilige Potenz der Basiszahl steht, die 0 bedeutet weiterhin, dass dort nichts steht. Ich werde das an einem Beispiel demonstrieren.
Die Dezimalzahl 13,6 soll in ein System mit der Basis 1,4 umgerechnet werden.
Als Erstes erstelle ich eine Tabelle mit den Potenzen der Basiszahl:
| ⋮ | |||
| 1,48 | = | 14 | ,75789056 |
| 1,47 | = | 10 | ,5413504 |
| 1,46 | = | 7 | ,529536 |
| 1,45 | = | 5 | ,37824 |
| 1,44 | = | 3 | ,8416 |
| 1,43 | = | 2 | ,744 |
| 1,42 | = | 1 | ,96 |
| 1,41 | = | 1 | ,4 |
| 1,40 | = | 1 | |
| 1,4−1 | = | 0 | ,71428571 |
| 1,4−2 | = | 0 | ,51020408 |
| 1,4−3 | = | 0 | ,36443149 |
| 1,4−4 | = | 0 | ,26030820 |
| 1,4−5 | = | 0 | ,18593443 |
| 1,4−6 | = | 0 | ,13281031 |
| 1,4−7 | = | 0 | ,09486451 |
| 1,4−8 | = | 0 | ,06776036 |
| 1,4−9 | = | 0 | ,04840026 |
| ⋮ |
Anschließend suche ich die höchste Stelle, die noch kleiner ist als meine gesuchte Zahl. Das ist die Stelle mit der Potenz 7, deren Wert 10,5413504 ist. An die 8. Stelle links vom Komma kommt also eine 1:
1 . . . . . . . , . .
Die Differenz zur Zahl 13,6 beträgt nun 13,6 − 10,5413504 = 3,0586496. Da die Potenzwerte an den nächsten Stellen (mit den Potenzen 6, 5 und 4) alle größer als diese Differenz sind, kommt an diese Stellen jeweils eine 0 und erst dann wieder eine 1:
10001 . . . , . .
Die Differenz zu 13,6 beträgt nun noch 13,6 − 10,5413504 − 2,744 = 0,3146496. Den nächstkleineren Potenzwert finde ich erst an der Stelle mit der Potenz −4. Ich fülle also alle oberhalb dieser Potenz liegenden Stellen mit Nullen auf und an die Stelle mit der Potenz −4 kommt eine 1:
10001000,00011,4
Die Differenz zu unserer gesuchten Zahl beträgt somit nur noch 13,6 − 10,5413504 − 2,744 − 0,2603082 = 0,0543414. Will ich noch genauer rechnen, dann muss ich mir nur den nächstkleineren Potenzwert aus meiner Tabelle suchen, dieser steht an der Stelle mit der Potenz −9. Die dazwischenliegenden Stellen kann ich wieder mit Nullen auffüllen:
10001000,0001000011,4
Ich mache die Probe und rechne:
| 1,47 | + | 1,43 | + | 1,4−4 | + | 1,4−9 | = | |
| 10,5413504 | + | 2,744 | + | 0,2603082 | + | 0,04840026 | = | 13,59405886 |
Wir liegen damit bereits sehr nahe an unserer gesuchten Zahl. Die Rechengenauigkeit würde durch das Hinzunehmen weiterer Stellen natürlich noch steigen.
|
Bei den Zahlen mit den Nullen und Einsen habe ich die Basis des Zahlensystems in Form einer kleinen, tiefergestellten Zahl dazugeschrieben. Dadurch besteht keine Verwechslungsgefahr mit einer Zahl im Dualsystem, die ja ebenfalls nur aus Nullen und Einsen besteht. Nur so zum Spaß rechne ich dieselbe Zahl 13,6 noch in zwei weitere Systeme um, deren Basis jeweils kleiner als 2 ist: Ich nehme einmal die Basis 1,2 und einmal die Basis 1,8. Beginnen wir mit dem kleineren Wert 1,2. Rechts von hier sieht man die Tabelle mit den Potenzen. Was uns sehr schnell auffällt, ist die Größe der Tabelle. Obwohl der größte und der kleinste Dezimalwert ähnlich groß sind wie in unserer Tabelle mit der Basis 1,4, brauchen wir viel mehr Zeilen. Sie »wächst langsamer«, da der jeweilige Wert statt um den Faktor 1,4 nur noch um den Faktor 1,2 ansteigt. Ansonsten ist aber kein wesentlicher Unterschied zu erkennen. Die einzelnen Rechenschritte für das Berechnen der Zahl im System mit der Basis 1,2 liste ich hier nicht auf, sondern schreibe gleich das Ergebnis hin (wer Lust hat, kann es nachrechnen): 100000000000000,0100000000000011,2
|
 |
|
Die Tabelle mit den Potenzwerten der Basis 1,8 sieht wie folgt aus:
| ⋮ | |||
| 1,85 | = | 18 | ,89568 |
| 1,84 | = | 10 | ,4976 |
| 1,83 | = | 5 | ,832 |
| 1,82 | = | 3 | ,24 |
| 1,81 | = | 1 | ,8 |
| 1,80 | = | 1 | |
| 1,8−1 | = | 0 | ,55555556 |
| 1,8−2 | = | 0 | ,30864198 |
| 1,8−3 | = | 0 | ,17146776 |
| 1,8−4 | = | 0 | ,09525987 |
| 1,8−5 | = | 0 | ,05292215 |
| 1,8−6 | = | 0 | ,02940119 |
| ⋮ |
Wie zu erwarten war, ist sie viel kleiner als die Tabelle für die Werte mit der Basis 1,2. Die errechnete Zahl ist
10011,0011011,8
| 1,84 | + | 1,81 | + | 1,80 | + | 1,8−3 | + | 1,8−4 | + | 1,8−6 | = | |
| 10,4976 | + | 1,8 | + | 1 | + | 0,17146776 | + | 0,09525987 | + | 0,02940119 | = | 13,5937288 |
Bei der Umrechnung in ein Zahlensystem mit einer Basis kleiner als 2 ist mir Folgendes aufgefallen:
Ich kann die meisten Zahlen auf verschiedene Weise hinschreiben, und dennoch bleibt ihr Wert gleich! Diese Behauptung ist im ersten Moment verblüffend und sollte unbedingt näher erklärt werden. Ich nehme das Beispiel mit der Basis 1,2 her, für das wir folgendes Ergebnis erhalten haben:
100000000000000,0100000000000011,2
Diese Zahl hätte ich genausogut auf folgende Weise hinschreiben können:
11000001000,0000010000010011,2
| 1,210 | + | 1,29 | + | 1,23 | + | 1,2−6 | + | 1,2−12 | + | 1,2−15 | = | |
| 6,1917364 | + | 5,1597804 | + | 1,728 | + | 0,3348980 | + | 0,1121567 | + | 0,0649055 | = | 13,5914769 |
Oder auf die folgende Weise:
1000010000001,000000000000000111,2
| 1,212 | + | 1,27 | + | 1,20 | + | 1,2−16 | + | 1,2−17 | = | |
| 8,91610045 | + | 3,5831808 | + | 1 | + | 0,05408789 | + | 0,04507324 | = | 13,59844238 |
Und auf noch viele andere Weisen ... Immer hätte das Ergebnis ziemlich genau dem Wert der Dezimalzahl 13,6 entsprochen. Je kleiner ich die Basiszahl wähle, desto mehr Möglichkeiten gibt es, den gleichen Zahlenwert auszudrücken. Wir können auch sagen: Desto mehr Redundanz ist im System enthalten. Zahlensysteme, deren Basis auf einer ganzen Zahl beruht, haben keine Redundanz, d. h. ich kann jeden Zahlenwert nur auf genau eine Weise hinschreiben.
Ich unternehme nun einen Versuch. Ich möchte herausfinden, auf wie viele unterschiedliche Arten ich einen bestimmten Zahlenwert aufschreiben kann. Ich probiere das auf’s Geratewohl mit der (Dezimal-)Zahl 12 und rechne sie in unterschiedliche Zahlensysteme um, deren Basiswert jeweils kleiner als 2 ist. In Bezug auf die Rechengenauigkeit begnüge ich mich damit, dass der Absolutwert der Abweichung vom exakten Ergebnis jeweils kleiner als 1 ist.
Als Basiswerte nehme ich 1,9, 1,8, 1,7, 1,6, 1,5, 1,4, 1,3 und 1,2.
Die entsprechenden Potenzentabellen sehen wie folgt aus:
| 1,94 | = | 13 | ,0321 | 1,85 | = | 18 | ,89568 | 1,75 | = | 14 | ,19857 | 1,66 | = | 16 | ,77722 | |||
| 1,93 | = | 6 | ,859 | 1,84 | = | 10 | ,4976 | 1,74 | = | 8 | ,3521 | 1,65 | = | 10 | ,48576 | |||
| 1,92 | = | 3 | ,61 | 1,83 | = | 5 | ,832 | 1,73 | = | 4 | ,913 | 1,64 | = | 6 | ,5536 | |||
| 1,91 | = | 1 | ,9 | 1,82 | = | 3 | ,24 | 1,72 | = | 2 | ,89 | 1,63 | = | 4 | ,096 | |||
| 1,90 | = | 1 | 1,81 | = | 1 | ,8 | 1,71 | = | 1 | ,7 | 1,62 | = | 2 | ,56 | ||||
| 1,80 | = | 1 | 1,70 | = | 1 | 1,61 | = | 1 | ,6 | |||||||||
| 1,60 | = | 1 | ||||||||||||||||
| 1,57 | = | 17 | ,08594 | 1,48 | = | 14 | ,75789 | 1,310 | = | 13 | ,78585 | 1,214 | = | 12 | ,83918 | |||
| 1,56 | = | 11 | ,39063 | 1,47 | = | 10 | ,54135 | 1,39 | = | 10 | ,60450 | 1,213 | = | 10 | ,69932 | |||
| 1,55 | = | 7 | ,59375 | 1,46 | = | 7 | ,52954 | 1,38 | = | 8 | ,15731 | 1,212 | = | 8 | ,91610 | |||
| 1,54 | = | 5 | ,0625 | 1,45 | = | 5 | ,37824 | 1,37 | = | 6 | ,27485 | 1,211 | = | 7 | ,43008 | |||
| 1,53 | = | 3 | ,375 | 1,44 | = | 3 | ,8416 | 1,36 | = | 4 | ,82681 | 1,210 | = | 6 | ,19174 | |||
| 1,52 | = | 2 | ,25 | 1,43 | = | 2 | ,744 | 1,35 | = | 3 | ,71293 | 1,29 | = | 5 | ,15978 | |||
| 1,51 | = | 1 | ,5 | 1,42 | = | 1 | ,96 | 1,34 | = | 2 | ,8561 | 1,28 | = | 4 | ,29982 | |||
| 1,50 | = | 1 | 1,41 | = | 1 | ,4 | 1,33 | = | 2 | ,197 | 1,27 | = | 3 | ,58318 | ||||
| 1,40 | = | 1 | 1,32 | = | 1 | ,69 | 1,26 | = | 2 | ,98598 | ||||||||
| 1,31 | = | 1 | ,3 | 1,25 | = | 2 | ,48832 | |||||||||||
| 1,30 | = | 1 | 1,24 | = | 2 | ,0736 | ||||||||||||
| 1,23 | = | 1 | ,728 | |||||||||||||||
| 1,22 | = | 1 | ,44 | |||||||||||||||
| 1,21 | = | 1 | ,2 | |||||||||||||||
| 1,20 | = | 1 | ||||||||||||||||
Basis 1,9 (2 Möglichkeiten):
| 11101,9 | = | 1,93 | + | 1,92 | + | 1,91 | = | 6,859 | + | 3,61 | + | 1,9 | = | 12,369 |
| 11011,9 | = | 1,93 | + | 1,92 | + | 1,90 | = | 6,859 | + | 3,61 | + | 1 | = | 11,469 |
Basis 1,8 (2 Möglichkeiten):
| 100101,8 | = | 1,84 | + | 1,81 | = | 10,4976 | + | 1,8 | = | 12,2976 |
| 100011,8 | = | 1,84 | + | 1,80 | = | 10,4976 | + | 1 | = | 11,4976 |
Basis 1,7 (2 Möglichkeiten):
| 101111,7 | = | 1,74 | + | 1,72 | + | 1,71 | + | 1,70 | = | 8,3521 | + | 2,89 | + | 1,7 | + | 1 | = | 12,9421 |
| 101101,7 | = | 1,74 | + | 1,72 | + | 1,71 | = | 8,3521 | + | 2,89 | + | 1,7 | = | 11,9421 |
Basis 1,6 (4 Möglichkeiten):
| 1000101,6 | = | 1,65 + 1,61 | = | 10 | ,48576 | + | 1,6 | = | 12,08576 | ||
| 110101,6 | = | 1,64 + 1,63 + 1,61 | = | 6 | ,55360 | + | 4,096 | + | 1,6 | = | 12,2496 |
| 110011,6 | = | 1,64 + 1,63 + 1,60 | = | 6 | ,55360 | + | 4,096 | + | 1 | = | 11,6496 |
| 101111,6 | = | 1,64 + 1,62 + 1,61 + 1,60 | = | 6 | ,55360 | + | 2,56 | + | 1,6 + 1 | = | 11,7136 |
Basis 1,5 (9 Möglichkeiten):
| 10000011,5 | = | 12,39063 | 1010101,5 | = | 12,46875 | 1001111,5 | = | 12,34375 | ||
| 10000001,5 | = | 11,39063 | 1010011,5 | = | 11,96875 | 111101,5 | = | 12,1875 | ||
| 1100001,5 | = | 12,65625 | 1001101,5 | = | 11,34375 | 111011,5 | = | 11,6875 |
Basis 1,4 (22 Möglichkeiten):
| 100001001,4 | = | 12,50135 | 10011001,4 | = | 12,23354 | 1101101,4 | = | 12,57984 | ||
| 100000111,4 | = | 12,94135 | 10010111,4 | = | 12,67354 | 1101011,4 | = | 12,17984 | ||
| 100000101,4 | = | 11,94135 | 10010101,4 | = | 11,67354 | 1101001,4 | = | 11,17984 | ||
| 100000011,4 | = | 11,54135 | 10010011,4 | = | 11,27354 | 1100111,4 | = | 11,61984 | ||
| 11000001,4 | = | 12,90778 | 10001111,4 | = | 11,88954 | 1011111,4 | = | 12,84224 | ||
| 10100101,4 | = | 12,77114 | 1110011,4 | = | 12,96384 | 1011101,4 | = | 11,84224 | ||
| 10100011,4 | = | 12,37114 | 1110001,4 | = | 11,96384 | 1011011,4 | = | 11,44224 | ||
| 10100001,4 | = | 11,37114 | ||||||||
Basis 1,3 (48 Möglichkeiten):
| 10000010001,3 | = | 12,80150 | 101100001,3 | = | 12,84388 | 11011001,3 | = | 12,42674 | ||
| 10000001001,3 | = | 12,29450 | 101010001,3 | = | 12,18478 | 11010101,3 | = | 12,03674 | ||
| 10000000111,3 | = | 12,90450 | 101001101,3 | = | 12,97778 | 11010011,3 | = | 11,73674 | ||
| 10000000101,3 | = | 11,90450 | 101001011,3 | = | 12,67778 | 11001111,3 | = | 12,52974 | ||
| 10000000011,3 | = | 11,60450 | 101001001,3 | = | 11,67778 | 11001101,3 | = | 11,52974 | ||
| 1010000001,3 | = | 12,98412 | 101000111,3 | = | 12,28778 | 10111101,3 | = | 12,86991 | ||
| 1001000011,3 | = | 12,87024 | 101000101,3 | = | 11,28778 | 10111011,3 | = | 12,56991 | ||
| 1001000001,3 | = | 11,87024 | 100110101,3 | = | 12,62795 | 10111001,3 | = | 11,56991 | ||
| 1000101001,3 | = | 12,70341 | 100110011,3 | = | 12,32795 | 10110111,3 | = | 12,17991 | ||
| 1000100101,3 | = | 12,31341 | 100110001,3 | = | 11,32795 | 10110101,3 | = | 11,17991 | ||
| 1000011001,3 | = | 12,04431 | 100101101,3 | = | 12,12095 | 10101111,3 | = | 11,67291 | ||
| 1000001111,3 | = | 12,14731 | 100101011,3 | = | 11,82095 | 10011111,3 | = | 11,01381 | ||
| 1000001101,3 | = | 11,14731 | 100100111,3 | = | 11,43095 | 1111111,3 | = | 12,75603 | ||
| 110000101,3 | = | 12,40166 | 100011111,3 | = | 12,46185 | 1111101,3 | = | 11,75603 | ||
| 110000011,3 | = | 12,10166 | 100011101,3 | = | 11,46185 | 1111011,3 | = | 11,45603 | ||
| 110000001,3 | = | 11,10166 | 11100101,3 | = | 12,69584 | 1110111,3 | = | 11,06603 |
Basis 1,2 (273 Möglichkeiten):
Es gibt unter den oben angegebenen Voraussetzungen 273 Möglichkeiten, die Dezimalzahl 12 mit einem System mit der Basis 1,2 darzustellen. Ich habe es unterlassen, eine noch kleinere Basiszahl als 1,2 zu verwenden (z. B. 1,1 oder gar 1,01), denn die Anzahl der Möglichkeiten steigt offensichtlich gewaltig an, je mehr sich die Basiszahl dem kleinstmöglichen Wert 1 nähert. Und dabei habe ich jeweils nur die Stellen links vom Komma berücksichtigt! Das war eine bewusste, vorläufige Einschränkung. Was passiert, wenn ich auch die Stellen rechts vom Komma berücksichtige? In allen Zahlensystemen steigt damit natürlich die Genauigkeit. Ich kann damit eine beliebige Genauigkeit erreichen. Allerdings gibt es noch einen anderen Effekt, der wichtig ist.
Um diesen Effekt zu zeigen, verwende ich als Beispiel die Umrechnung der Dezimalzahl 12 in das System mit der Basis 1,4. Zunächst erweitere ich meine Potenzen-Tabelle »nach unten« in den Bereich der negativen Potenzen:
| ⋮ | |||
| 1,48 | = | 14 | ,75789 |
| 1,47 | = | 10 | ,54135 |
| 1,46 | = | 7 | ,52954 |
| 1,45 | = | 5 | ,37824 |
| 1,44 | = | 3 | ,8416 |
| 1,43 | = | 2 | ,744 |
| 1,42 | = | 1 | ,96 |
| 1,41 | = | 1 | ,4 |
| 1,40 | = | 1 | |
| 1,4−1 | = | 0 | ,7142857 |
| 1,4−2 | = | 0 | ,5102041 |
| 1,4−3 | = | 0 | ,3644315 |
| 1,4−4 | = | 0 | ,2603082 |
| 1,4−5 | = | 0 | ,1859344 |
| 1,4−6 | = | 0 | ,1328103 |
| 1,4−7 | = | 0 | ,0948645 |
| 1,4−8 | = | 0 | ,0677604 |
| 1,4−9 | = | 0 | ,0484003 |
| 1,4−10 | = | 0 | ,0345716 |
| 1,4−11 | = | 0 | ,0246940 |
| 1,4−12 | = | 0 | ,0176386 |
| 1,4−13 | = | 0 | ,0125990 |
| 1,4−14 | = | 0 | ,0089993 |
| 1,4−15 | = | 0 | ,0064305 |
| 1,4−16 | = | 0 | ,0045915 |
| 1,4−17 | = | 0 | ,0032796 |
| 1,4−18 | = | 0 | ,0023426 |
| 1,4−19 | = | 0 | ,0016733 |
| 1,4−20 | = | 0 | ,0011952 |
| 1,4−21 | = | 0 | ,0008537 |
| 1,4−22 | = | 0 | ,0006098 |
| 1,4−23 | = | 0 | ,0004356 |
| 1,4−24 | = | 0 | ,0003111 |
| 1,4−25 | = | 0 | ,0002222 |
| 1,4−26 | = | 0 | ,0001587 |
| 1,4−27 | = | 0 | ,0001134 |
| 1,4−28 | = | 0 | ,0000810 |
| 1,4−29 | = | 0 | ,0000578 |
| 1,4−30 | = | 0 | ,0000413 |
| 1,4−31 | = | 0 | ,0000295 |
| 1,4−32 | = | 0 | ,0000211 |
| 1,4−33 | = | 0 | ,0000151 |
| 1,4−34 | = | 0 | ,0000108 |
| 1,4−35 | = | 0 | ,0000077 |
| 1,4−36 | = | 0 | ,0000055 |
| 1,4−37 | = | 0 | ,0000039 |
| 1,4−38 | = | 0 | ,0000028 |
| 1,4−39 | = | 0 | ,0000020 |
| 1,4−40 | = | 0 | ,0000014 |
| 1,4−41 | = | 0 | ,0000010 |
| 1,4−42 | = | 0 | ,0000007 |
| ⋮ |
Das erste Ergebnis bei unserem »ersten Durchgang« der Umrechnung ins System mit der Basis 1,4, dessen Wert knapp unterhalb von 12 war, lautete
100000101,4 = 11,94135
Um die Zahl 12 exakt zu erreichen, fehlt also noch die Differenz 12 − 11,94135 = 0,05865. Ich füge daher an der 9. Stelle rechts vom Komma eine 1 hinzu und die Differenz beträgt nur noch 0,05856 − 0,0484003 = 0,0101597. Unser wesentlich genaueres Ergebnis heißt nun
10000010,00000000011,4 = 11,9898403
Eine weitere 1 an der 14. Stelle rechts vom Komma verbessert es weiter.
10000010,0000000001000011,4 = 11,9988396
An der 21. Stelle rechts vom Komma eine weitere 1 drangehängt ergibt
10000010,00000000010000100000011,4 = 11,9996933
und dann hängen wir auch noch an der 25.
10000010,000000000100001000000100011,4 = 11,9999155
und an der 28. Stelle eine weitere 1 dran:
10000010,000000000100001000000100010011,4 = 11,9999965
Ich bin dabei so vorgegangen, dass ich nach dem Komma jeweils den ersten Potenzwert genommen habe, der etwas kleiner als die noch vorhandene Differenz zur gesuchten Zahl 12 war. Ich hätte aber auch statt des Wertes mit der Potenz −9 erst den Wert mit der Potenz –10 nehmen können, da danach noch genügend Potenzwerte kommen, deren Summe locker ausreicht, um die Differenz zu 12 aufzufüllen. Selbst wenn ich erst mit der Potenz –12 weitergemacht hätte, wäre das kein Malheur gewesen. Denn
1,4−12 + 1,4−13 + 1,4−14 + 1,4−15 + 1,4−16 = 0,0502564
ist bereits größer als 1,4−9 = 0,0484003. Die Potenzwerte wachsen schneller als nötig. Die Konsequenz daraus ist, dass es unendlich viele Möglichkeiten gibt, wie eine bestimmte Zahl geschrieben werden kann. Solange ich mich auf die positiven Potenzwerte beschränke, gibt es nur eine begrenzte Anzahl von Möglichkeiten. Verwende ich jedoch auch die negativen Potenzwerte mit beliebig vielen Stellen nach dem Komma, dann steigt die Anzahl der Möglichkeiten ins Unendliche.
– – –
Im Folgenden werde ich die Anzahl der Möglichkeiten untersuchen, die Dezimalzahl 12 in einem »Φ-System« darzustellen. Wir haben vorhin u. a. bereits die Möglichkeiten mit den Basiszahlen 1,6 und 1,7 untersucht – für 1,7 haben wir 2 Möglichkeiten und für 1,6 haben wir 4 Möglichkeiten gefunden. Als Einschränkung für die Genauigkeit des Ergebnisses bei der Berechnung haben wir eine Abweichung von kleiner als 1 festgelegt. Mit sinkender Größe der Basiszahl stieg die Anzahl der Möglichkeiten.
Da Φ = 1,618... etwas größer als 1,6 ist, erwarte ich ein Ergebnis zwischen 2 und 4 Möglichkeiten.
Als Erstes lege ich die Potenzentabelle für die Basis Φ an:
| ⋮ | |||
| Φ6 | = | 17 | ,94427191 |
| Φ5 | = | 11 | ,09016994 |
| Φ4 | = | 6 | ,85410197 |
| Φ3 | = | 4 | ,23606798 |
| Φ2 | = | 2 | ,61803399 |
| Φ1 | = | 1 | ,61803399 |
| Φ0 | = | 1 | |
| ⋮ |
Der erste Wert ist schnell gefunden. Er ist
100000Φ = Φ5 = 11,09017
Die Abweichung zur gesuchten Zahl 12 ist bereits kleiner als 1. Der nächste gefundene Wert ist
11000Φ = Φ4 + Φ3 = 6,85410 + 4,23607 = 11,09017
Schließlich gibt es noch eine weitere Möglichkeit:
10110Φ = Φ4 + Φ2 + Φ1 = 6,85410 + 2,618034 + 1,618034 = 11,09017
Wir erhalten als Ergebnis somit 3 Möglichkeiten. Schreiben wir diese 3 Möglichkeiten nochmal schön untereinander auf:
| 100000Φ | = | Φ5 | = | 11,09017 |
| 11000Φ | = | Φ4 + Φ3 | = | 11,09017 |
| 10110Φ | = | Φ4 + Φ2 + Φ1 | = | 11,09017 |
3-mal das exakt gleiche Ergebnis!!
War das Zufall oder tritt ein solches Ergebnis auch bei anderen Zahlen auf? Das möchte ich jetzt gleich wissen. Ich untersuche daher auch noch die Anzahl der Möglichkeiten für eine andere Zahl – und nehme dafür die Zahl 16,5.
Hier die 3 Ergebnisse:
| 101001Φ | = | Φ5 + Φ3 + Φ0 | = | 16,32624 |
| 100111Φ | = | Φ5 + Φ2 + Φ1 + Φ0 | = | 16,32624 |
| 11111Φ | = | Φ4 + Φ3 + Φ2 + Φ1 + Φ0 | = | 16,32624 |
Wenn man genau hinschaut, dann kann man sehen, dass es einen einfachen Grund gibt, warum die Ergebnisse immer identisch sein müssen:
Darin ist die gesamte »Entstehungsgeschichte« der Zahl Φ enthalten:
Nimm etwas und gib etwas Anderes dazu. Das Ergebnis ist etwas Neues.
Das machst du mit dem Anderen und dem Neuen wieder.
Beliebig oft.
Eine Potenz von Φ ist immer die Summe der beiden vorhergehenden Potenzen! Also ist z. B.
Φ3 + Φ4 = Φ5
und das ist der Grund, warum
| 101001Φ | = | Φ5 + Φ3 + Φ0 | = | 16,32624 |
| 100111Φ | = | Φ5 + Φ2 + Φ1 + Φ0 | = | 16,32624 |
und
| 100111Φ | = | Φ5 + Φ2 + Φ1 + Φ0 | = | 16,32624 |
| 11111Φ | = | Φ4 + Φ3 + Φ2 + Φ1 + Φ0 | = | 16,32624 |
zu identischen Ergebnissen führen müssen.
~~~ ~~~
Mein Freund ist seit gestern wieder zurück von seinem Urlaub und ich nütze daher die Gelegenheit, ihn ein wenig zum Rechnen und Zeichnen einzuspannen.
|» Was hältst du davon?
«| Nur zu, ich bin gut ausgeruht! Wobei soll ich dir denn helfen?
|» Um dir das zu beschreiben, muss ich erst ein wenig ausholen. Wir haben bei der Beschäftigung mit unseren »Zahlensystemen« mit einem Basiswert kleiner als 2 und größer als 1 festgestellt, dass wir damit genausogut jede beliebige Zahl darstellen können wie mit Zahlensystemen, deren Basis eine natürliche Zahl größer oder gleich 2 ist. Allerdings liefern die Zahlen in diesen Systemen immer viele bzw. sogar unendlich viele Möglichkeiten, eine Zahl darzustellen. Wenn wir uns darauf einigen, dass wir die Umrechnung in unser System mit der kleinen Basis immer auf eine ganz bestimmte Weise vornehmen, dann haben wir zumindest eine Art »Standard«, von dem aus wir Vergleiche ziehen können.
Ich möchte nämlich wissen, ob es irgendein Muster gibt, nach welchem sich natürliche Zahlen (also ganze Zahlen) bilden. Für unser »Standard-Verfahren« schlage ich vor, dass wir – so wie ich es bereits vorhin gemacht habe – jeweils die erste Möglichkeit hernehmen, um eine Zahl zu bilden. So wie ich es bei der Umrechnung der Zahl 13,6 in ein System mit der Basis 1,4 gemacht habe.
Da die Ergebnisse für die Umrechnung immer in einer »dualen« Form vorliegen (nur die Ziffern 0 und 1 müssen verwendet werden), kannst du sie auch als eine Art »Plot« darstellen, also so, dass du einen schwarzen Punkt für eine 1 ausgibst und für eine 0 das Papier einfach weiß lässt.
«| Das klingt nicht weiter schwierig.
|» Das dachte ich mir. Allerdings hat die Sache einen klitzekleinen Haken – ohne diesen hätte ich während deines Urlaubs das Problem längst selber gelöst. Ich möchte nämlich, dass du eine Software verwendest, welche die Berechnungen auf mindestens 100 Dezimalstellen genau durchführt. Möglicherweise brauchen wir sogar eine noch höhere Genauigkeit.
«| 100 Dezimalstellen? Das geht nicht, mein Excel rechnet nur mit einer Genauigkeit von 15 Stellen. Ich besitze zwar auch einen ultragenauen Taschenrechner, aber selbst dessen Genauigkeit ist auf 32 Stellen begrenzt.
|» Du bist doch Programmierer ...
«| Ja. Aber was du da verlangst, ist alles andere als einfach. Schließlich ...
|» (Lacht) Wenn’s einfach wäre, hätte ich es längst selber erledigt!
«| Bis wann brauchst du es?
|» Bis gestern.
«| Na klar ... reicht ein silbernes Tablett oder soll ich es dir auf einem goldenen servieren?
|» Mir reicht ein gewöhnliches Holzbrett.
«| (Seufzt) Also gut. Ich erfülle dir deinen Wunsch. Irgendwie werde ich das schon hinbekommen.
|» Juhuuu!
~~~ ~~~ Einige Tage später ~~~ ~~~
«| Ich hab’s!
|» Was?
«| Das Programm! Mein Excel kann jetzt auf beliebig viele Stellen genau rechnen! Allerdings ist die Rechengeschwindigkeit nicht gerade berauschend.
|» Das stört mich nicht. Solange wir die Rechenzeit nicht in Wochen ausdrücken müssen ...
«| Nein, so schlimm ist es nicht. Aber für größere Diagramme kann es schon sein, dass sich mein Computer ein paar Stunden lang ins Zeug legen muss.
|» Dann verhelfen wir ihm gleich zu ein paar vergnüglichen Rechenstunden. Ich würde gerne einen Probegalopp mit der Basiszahl 1,5 machen.
~~~ ~~~ Etwas später ~~~ ~~~
«| Schau her. Ich habe die Punkte, die eine 1 darstellen, in Form von schwarzen Quadraten dargestellt:
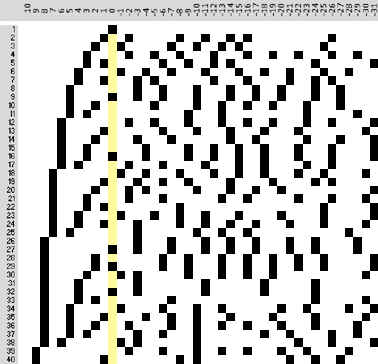
Bild 17: Basis = 1,5
Oberhalb davon habe ich die Potenzen aufgetragen, links siehst du die natürlichen Zahlen, die ich berechnet habe. In dem Muster habe ich die ganzen Zahlen von 1 bis 40 im »Dualsystem« mit der Basis 1,5 dargestellt. Picken wir uns die Dezimalzahl 19 etwas vergrößert heraus:

Bild 18
|» Genau so habe ich mir das vorgestellt! Allerdings ist die Genauigkeit noch nicht so hoch wie von mir gewünscht.
«| Das ist kein Problem, ich wollte dir erst mal nur das Prinzip zeigen, wie meine Lösung aussieht. Später kann ich die Tabelle in alle Richtungen beliebig erweitern.
Die natürliche Zahl 19 sieht im 1,5er-System also wie folgt aus:
10000010,00100100100001000010000101000001,5 =
1,57 + 1,51 + 1,5−3 + 1,5−6 +
1,5−9 + 1,5–14 + 1,5–19 + 1,5−24 +
1,5−26 =
18,9999999713602206099300405
|» Das ist bereits ziemlich genau! Und ich habe es sicherheitshalber mit deinem supergenauen Taschenrechner nachgerechnet – er kommt zum gleichen Ergebnis! Diese noch wesentlich höhere Genauigkeit brauche ich aber nicht für die Zahl selbst (diese ist gar nicht so interessant), sondern für das Muster, das eventuell erkennbar wird, wenn ich die Veränderung über eine Vielzahl von Zahlen vergleichen kann. Ganz speziell interessieren mich fürs Erste die »Randbereiche« knapp unterhalb der Basis 2 und knapp oberhalb der Basis 1.
«| Dann schlage ich vor, wir beginnen mit der Basis 1,01:

Bild 19: Basis = 1,01
|» Die einzelnen Punkte sind jetzt aber sehr klein!
«| Weil es so viele sind! Die Tabelle enthält »nach unten« die natürlichen Zahlen von 1 bis 420. Von der grauen Null-Linie nach links sind die positiven Potenzen bis 630 aufgetragen, rechts davon die negativen Potenzen bis −312. Erhöht man die Basis geringfügig, dann krümmt sich die »äußere Kurve« stärker nach unten. In späterer Folge werden dann auch immer mehr »innere Kurven« sichtbar, die sich ebenfalls zunehmend stärker krümmen.
Das Ergebnis im gleichen Maßstab für weitere Basiswerte von 1,02 bis 1,10 zum Durchklicken:
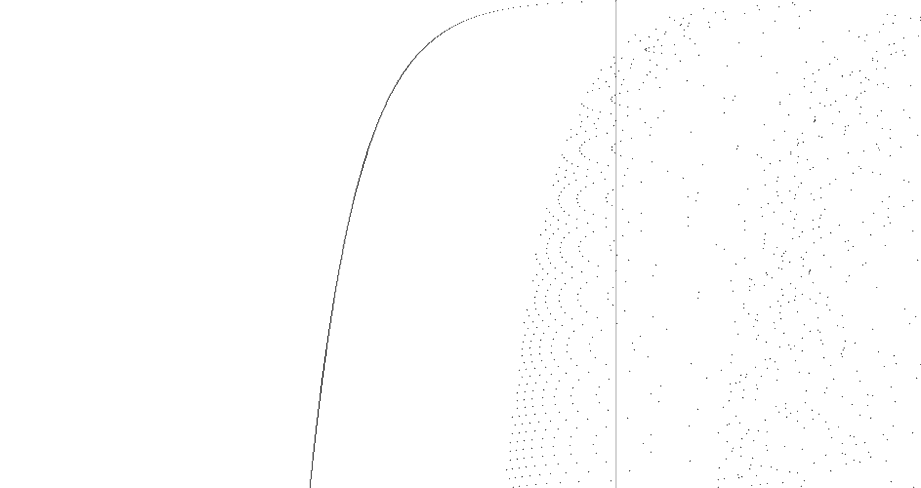
Oberhalb von 1,10 vergrößern wir die Darstellung und wählen den Ausschnitt so, dass in horizontaler Richtung die Potenzen von +40 bis −150 und in vertikaler Richtung (nach unten) die natürlichen Zahlen von 1 bis 200 aufgetragen werden. In der weiteren Folge erhöhen wir die Basis-Werte stufenweise um jeweils 0,05. Bitte wieder auf die Pfeile klicken!
Bild 50
|» Das übriggebliebene Muster entspricht genau den (ausschließlich positiven) Potenzen der Zahl 2 und somit dem Dualsystem, wie es unsere Computer verwenden. In der Technik werden solche schwarz-weißen Muster verwendet, um mit Hilfe von Laserstrahlen z. B. Wegstrecken oder (wenn das gleiche Muster kreisförmig angeordnet ist) Winkel zu messen.
Am anderen Ende unseres Spektrums zwischen 1 und 2, auf der Seite der 1, haben wir die einzelnen Punkte sehr weit auseinandergedehnt gesehen (Bild 19). Wenn wir den Wert unserer Basis sehr, sehr knapp oberhalb von 1 annehmen, dann kommen die einzelnen Punkt sehr, sehr weit voneinander entfernt zu liegen.
Nehmen wir beispielsweise den (gar nicht so knappen) Wert 1,000004 als Basis. Dann befindet sich für die Zahl 1 genau eine 1 auf der Nulllinie (so wie für alle anderen Basiswerte auch). Für die Zahl 2 jedoch liegt ein Punkt unterhalb der Potenz +173.287 und der nächste Punkt unterhalb der Potenz −3.422.500 . Weitere Punkt liegen noch sehr viel weiter entfernt auf der Seite der negativen Potenzen. Ich habe diese Werte mit meinem Taschenrechner berechnet, der negative Wert weist daher eine Ungenauigkeit in der Größenordnung von ±100 auf, was ich als vernachlässigbar betrachte.
«| Was wir nicht vergessen sollten: Im Grenzbereich zur Basis 1 gibt es eine Besonderheit. Wenn wir den Basiswert als exakt 1 annehmen, dann fallen sämtliche Punkte schlagartig völlig in sich zusammen, sodass im Bereich der positiven Potenzen nur noch ein tiefschwarzes Dreieck übrigbleibt:

![]() Basis = 1 (exakt)
Basis = 1 (exakt)
ODER:
Genausogut können die schwarzen Punkte irgendwo unterhalb der positiven Potenzen bis in die Gegend des Unendlichen herumschwirren. Es muss lediglich gewährleistet sein, dass in der Zeile 1 nur ein Punkt zu finden ist, in der Zeile 2 müssen es genau 2 Punkte sein, usw. Und es dürfen natürlich nicht mehrere Punkte an ein- und derselben Stelle zu liegen kommen. Der Grund für die Beliebigkeit der Position unterhalb der Potenzen ist trivial: Die Zahl 1 kann ich beliebig oft mit sich selbst multiplizieren, sie bleibt stets sie selbst: 1.
Der Bereich der negativen Potenzen (rechts von der Nulllinie) bleibt genauso wie beim Basiswert 2 in Bild 50 (letztes Bild »Y«) komplett weiß.
Brauchbar ist eine solche Konstruktion natürlich nicht. Denn eine Zahl im Zahlensystem mit der Basis 1 heißt nichts anderes, als dass z. B. die Dezimalzahl 19 auf folgende Weise geschrieben wird:
1910 = 11111111111111111111
Das wäre, als würden wir mit unseren Fingern und Zehen zählen – 19 würden wir gerade noch schaffen ...
|» Nehmen wir nun jenen Bereich unter die Lupe, ab dem die Dichte der einzelnen Punkte so groß wird, dass diese den Mindestabstand von 1 zueinander nicht mehr einhalten können.
Dieser Übergang muss irgendwo im Bereich zwischen den Basiszahlen 1,6 und 1,65 auftreten. Uns dämmert natürlich bereits, wo dieser Bereich genau liegen wird ...
Doch greifen wir nicht vor – tasten wir uns ganz seriös Schritt für Schritt heran. Auf diese Weise sehen wir auch, welche Veränderungen stattfinden, während wir uns unserem Ziel immer mehr annähern.
Hilfst du mir wieder mit deiner Software?
«| Gerne! Mein Computer scharrt schon mit den Hufen.
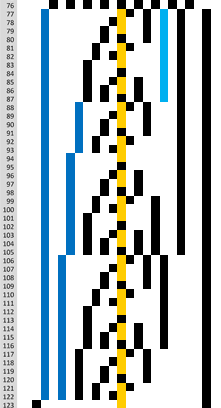
Bild 51

Bild 61: Basis = Φ = 1,61803398874989... für alle natürlichen Zahlen von
1 bis 1000
Bild vergrößern
|
Bild 62 |
 |
Nehmen wir zunächst einmal ein paar Stichproben und kontrollieren, ob die Werte des Musters auch tatsächlich lauter ganze Zahlen liefern. Ich wähle für die Stichproben die Zahlen 14, 23, 65 und 119. 14 = Φ5 + Φ2 + Φ−3 + Φ−6 Mein Taschenrechner, in dem ich Φ als Konstante mit einer Genauigkeit von 12 Dezimalstellen gespeichert hatte, sagt dazu: Ja, es stimmt! «| Wir können das auch mithilfe unserer vereinfachten Methode der Potenzenberechnung überprüfen und verwenden dafür unsere Berechnungs-Tabelle:
|» Perfekt! Überprüfe bitte auch noch die anderen Stichproben.
«| Alles hat seine Richtigkeit! Die »Φ-Anteile« werden jeweils 0, sodass nur die ganzzahligen Anteile übrigbleiben, und diese ergeben immer genau die gesuchte ganze Zahl. |
|
Bild 63 |
 |
|» Wie lang sind denn die einzelnen »Streifen« in unserem Muster? Gibt es in dieser Hinsicht eine bestimmte Gesetzmäßigkeit? «| Ja, die gibt es. Ich habe in Bild 63 (links) für’s Erste die Länge der Streifen der äußeren »Hülle« eingetragen. Was sofort zu sehen ist, ohne dass man die Längen abzählen muss: Die Hüllstreifen auf der »Innenseite« (rechts von der Nulllinie, unterhalb der negativen Potenzen) haben jeweils die Länge der zwei gegenüberliegenden Streifen auf der »Außenseite«. Wenn man die Länge der Streifen misst, dann stellt sich heraus, dass »außen« die Längen jeweils abwechselnd um 1 größer oder um 1 kleiner als die Zeilensummen im Phi-Dreieck sind (Tabelle 4). Diese Zeilensummen entsprechen auch, wie wir bereits wissen, den ganzzahlig gerundeten Potenzen von Φ bzw. den Gliedern der Lucas-Folge.
|» Du hast in deiner Liste den Wert für die erste 1 nicht eingetragen! Bild 63 beginnt mit 1 • 1 • 2 • 2 • 5 • 6 • 12 ..., deine Liste jedoch mit 1 • 2 • 2 • 5 • 6 • 12 ... «| [Seufzt] Du hast wie meistens recht. Aber der Wert, der dort hingehört, hat mich ein wenig irritiert. |
|» Das ist noch lange kein Grund, ihn heimlich unter den Tisch fallen zu lassen. »Anfangswerte« in unseren Reihen, Tabellen und Bildern sind ohnehin meistens irgendwelche »Löcher« oder nehmen gleichzeitig unterschiedliche Werte an.
«| Das ist auch hier der Fall. Der Wert an der ersten Stelle ist nämlich 0:
| 1 | = | −1 | + | 1 = 0 |
| 1 | = | 2 | − | 1 |
| 2 | = | 1 | + | 1 |
| 2 | = | 3 | − | 1 |
| 5 | = | 4 | + | 1 |
| 6 | = | 7 | − | 1 |
| ⋮ | ⋮ | |||
Auf der »Innenseite« entsprechen die Streifenlängen übrigens genau den jeweils zweiten Werten der Lucas-Folge. Und der erste Wert ist konsequenterweise auch wieder »falsch«:
| 2 | → | 1 |
| 1 | ||
| 3 | → | 3 |
| 4 | ||
| 7 | → | 7 |
| 11 | ||
| 18 | → | 18 |
| 29 | ||
| 47 | → | 47 |
| 76 | ||
| 123 | → | 123 |
| ⋮ | ⋮ |
|
Bild 64 |
 |
|» Kannst du uns Näheres über die Entstehung der Längen auf der Innenseite sagen? Es sind ja auch andere Längen als jene auf der »Außenhülle« vorhanden. «| Das stimmt. Es gibt dort alle Werte der Lucas-Folge. Die Lucas-Folgen wachsen allerdings im Gegensatz zur Außenseite nicht »entlang der Nulllinie« sondern fächerförmig »quer zur Nulllinie«, wobei die Zweige des Fächers abwechselnd nach oben und unten wachsen. Ich bezeichne ab sofort die Elemente auf der Außenseite (positive Potenzen) als Ast und jene auf der Innenseite (negative Potenzen) als Fächer (Bild 64 – links). Der erste Wert (1) ist wie immer »falsch«. Er müsste entsprechend der Lucas-Folge den Wert 2 haben. Allerdings liegt dieser erste Wert auf der Nulllinie und teilt sich diese Position mit einem »Ast der Länge 1« in Richtung Außenseite. Untersucht man die Entstehung der Äste genauer, stellt man fest, dass diese jeweils an der Nulllinie beginnend nach außen und nach unten wachsen. Man kann sich das so vorstellen, dass sie »nach außen gedrückt« werden, und zwar so, dass immer ein Mindestabstand von 1 zum äußeren Ast hin gewährleistet ist. Das geschieht so lange, bis kein Ast mehr innerhalb der Begrenzung des äußersten Astes Platz hat. Dann weicht der äußerste Ast auf eine neue Ebene aus (die Potenz des Abschnitts wird um 1 erhöht), und von innen her wachsen weitere Äste nach, solange, bis wieder der gesamte Raum innerhalb des äußersten Astes mit den neuen Ästen aufgefüllt ist. |» Ich habe Schwierigkeiten, mir dieses Wachstum deiner Äste vorzustellen. Zeichne mir das bitte ein wenig detaillierter auf! «| Gerne. Ich beginne mit der ganzen Zahl 1 und arbeite mich von dort aus weiter voran. Die »Innenseite« interessiert uns im Moment noch nicht, daher konzentriere ich mich für’s Erste nur auf die Außenseite mit den positiven Potenzen. Die Zahl 1 entspricht dem Ursprung des gesamten Musters, sie liegt genau auf der Nulllinie und ist »wie üblich falsch«, aber genau das ist an dieser Stelle wohl richtig ... |
|
Bild 65 |
Der erste Ast, der zu wachsen beginnt, ist der äußere »Hüllen-Ast«. Er springt unmittelbar nach seinem Ursprung auf der Nulllinie auf eine neue Ebene (mit der Potenz 1). Von dort aus hat er die Tendenz, auf dieser Potenzlinie zu bleiben und geradewegs nach unten weiterzuwachsen (wie in Bild 66 durch das graue Quadrat angedeutet). |
|
Bild 66 |
Allerdings muss mit jedem Schritt nach unten ein weiteres »Teilstück« dazukommen, das wiederum von der Nulllinie aus zu wachsen beginnt. Ein solches Teilstück hat unterhalb des äußeren Astes aber nicht Platz, da es damit gegen die Regel des Mindestabstands von 1 verstoßen würde. |
|
Bild 67 |
Also findet das Wachstum nicht an einer neuen Astwurzel auf der Nulllinie statt, sondern am äußeren Ast, der damit auf eine neue Ebene (mit der Potenz 2) ausweicht (Bild 67). |
|
Bild 68 |
Jetzt erst kann der äußere Ast auf dieser Ebene bleiben und nach unten weiterwachsen, denn nun hat auf der Nulllinie eine neue Astwurzel Platz, ohne irgendwo den äußeren Ast zu berühren (Bild 68). |
|
Bild 69 |
Der neue Ast will nun von der Nulllinie aus weiterwachsen, scheitert aber an der Hürde des Mindestabstands. Also ist sein Wachstum bereits beendet und es ist wieder der äußere Ast an der Reihe zu wachsen – er tut dies auf einer neuen Ebene mit der Potenz 3 (Bild 69). |
|
Bild 70 |
Von dort aus kann er wieder gerade nach unten wachsen, da unterhalb von ihm genügend Platz für einen neuen Trieb vorhanden ist (Bild 70). Allerdings beginnt dessen Wachstum diesmal nicht auf der Nulllinie sondern bereits eine Ebene höher. Der Grund für diese »Zusatz-Regel« ist noch nicht sichtbar und wir lassen unser Pflänzchen vorerst ein paar weitere Schritte wachsen – vielleicht wächst damit auch unsere Erkenntnis. |
|
Bild 71 |
In Bild 71 sehen wir, dass der äußere Ast bereits wieder eine neue Ebene erklommen hat (auf der Potenzlinie 4), da unterhalb von ihm das neue Ästchen nicht mehr weiterwachsen konnte. |
|
Bild 72 |
Erst in Bild 72 kann wieder ein neuer Trieb zu wachsen beginnen, ohne dass er einen anderen Ast berührt. Diesmal treibt er wieder direkt auf der Nulllinie aus – |
|
Bild 73 |
und findet endlich auch Platz für weiteres Wachstum unterhalb des Außenastes, ohne diesen zu berühren. Dieser kann daher auf seiner Linie bleiben und geradeaus nach unten weiterwachsen (Bild 73). |
|
Bild 74 |
Das neue Ästchen findet ebenfalls Platz für weiteres Wachstum, allerdings auf der nächsthöheren Ebene, während der Außenast seine Reise nach unten immer noch geradlinig fortsetzen kann. Es findet nach wie vor keine Berührung zwischen den Ästen statt (Bild 74). |
|
Bild 75 |
In der weiteren Folge kann dann sogar der innere Ast zum ersten Mal nicht nach außen sondern nach unten hin weiterwachsen, da unterhalb von ihm auf der Nulllinie die Wurzel eines dritten Astes Platz findet, ohne ihn zu berühren (Bild 75). Wir sehen nun, dass die Potenzen 4, 2 und 0 alle besetzt sind und daher im nächsten Schritt der äußere Ast auf der nächsten Ebene (Ebene 5) weiterwachsen muss. |
|
Bild 76 |
Mit Bild 76 überspringe ich einen Wachstumsschritt und wir sehen in der Zeile 13, dass dort der nächste »neue« Ast auf der Potenzebene 1 eine Wurzel bildet und nicht auf der Nulllinie. Hier tritt also offensichtlich zum zweiten Mal die »Zusatz-Regel« in Kraft, die wir erstmals in Bild 70 auf der Zeile mit der Zahl 6 beobachten konnten. |
|
Bild 77 |
Die nächsten beiden Schritte sind ziemlich offensichtlich – der äußere Ast wächst weiter nach unten, der innere Ast treibt zunächst in Zeile 14 auf eine höhere Ebene (Ebene 2) aus und danach bildet sich auf Zeile 15 ein neuer Trieb auf der Nulllinie (Bild 77). Die weitere Entwicklung unseres Musters ist nun bereits absehbar. Einzig den Grund für die »Zusatz-Regel« haben wir noch nicht genau verstanden. |
Wenn wir ausschließen wollen, dass diese Regel irgendetwas mit der Länge der »Ast-Teilstücke« zu tun hat, sondern dass der Grund einzig in der Verdrängung von innen nach außen unter Einhaltung eines Mindestabstands von 1 zu finden ist, dann haben wir offensichtlich noch etwas übersehen.
|» Die Innenseite! Wir haben die Innenseite bisher noch nicht berücksichtigt! Schau dir die Positionen an, an welcher die »Fächer« zu wachsen beginnen. Am besten markierst du sie mit einem weißen Punkt.
|
Bild 78 |
«| Erledigt! (Bild 78) |» Bist du sicher, dass du wirklich alle Fächerwurzeln eingezeichnet hast? «| Wenn du eine Frage auf diese Weise stellst, dann werde ich unsicher ... Meinst du, ich habe irgendeine Wurzel übersehen? |» Ich denke schon. Meiner Ansicht nach solltest du alle Punkte auf der Nulllinie markieren, denn sie stellen alle eine Fächerwurzel dar. Auf der Nulllinie scheinen die Gesetze des Ursprungs zu gelten. Dort – und nur dort – können sich die beiden Seiten problemlos überlagern. |
Und tatsächlich scheint bei unserem »Phi-Muster« jeder Punkt auf der Nulllinie eine Überlagerung von Ast- und Fächerwurzel zu sein. Gehen wir die Punkte, die auf der Nulllinie liegen, einzeln durch und schauen wir, ob sie die Kriterien sowohl für die Außen- als auch für die Innenseite erfüllen.
«| Ich beginne mit der Zahl 1. Deren einziger Punkt bildet zweifellos die Wurzel für den gesamten äußeren Ast (der sich übrigens bis ins Unendliche erstreckt). Gleichzeitig ist der Punkt aber wohl auch das kleinste Teilstück der Hülle auf der Innenseite (siehe Bild 63).
Der nächste Punkt auf der Nulllinie ist der Zahl 4 zugeordnet. Er ist bereits mit einem weißen Punkt gekennzeichnet und erfüllt die Kriterien für eine Astwurzel (siehe Bild 68), so wie er auch eindeutig die Wurzel eines Fächers ist.
Der der Zahl 8 zugeordnete Null-Punkt ist wieder eindeutig die Wurzel eines Astes. Gleichzeitig spricht aber auch nichts dagegen, dass er die Wurzel eines Fächers darstellt, der nur einen einzigen Zweig ausgebildet hat (den auf der Nulllinie). Einen weiteren Zweig kann er nicht bilden, da ein solcher bereits den Nachbar-Fächer berühren würde (auf Zeile 9, Potenz −2). Fächer verzweigen sich ab ihrer Wurzel grundsätzlich zuerst nach unten, dann nach oben, und so weiter.
Wenn wir die Innenseite von der Zahl 1 ausgehend über 2, 3, 4, usw. abschreiten, so können wir im Gegensatz zu den Ästen auf der Außenseite nicht immer sofort angeben, wie weit ein Fächer an einer bestimmten Stelle nach rechts wachsen kann. Wenn wir am Nullpunkt der Zahl 8 angelangt sind, wissen wir noch nichts von der Existenz des nächsten Fächers, der seinen Ursprung am Nullpunkt der Zahl 11 hat, obwohl wir bereits ab der Zeile 5 seinem äußeren Zweig begegnet sind. Auf der Innenseite können wir also nicht erwarten, in gleicher Weise wie die Äste Schritt für Schritt unsere Fächer zu finden.
Es gibt jedoch eine andere Methode, wie wir unsere Fächer eindeutig finden können, wenn wir von 1 beginnend die Zeilen nach unten hin erkunden. Wir gehen für diesen Zweck immer von der Außenhülle nach innen und nehmen also den umgekehrten Weg. Denn wie schon gesagt erscheint der äußere Zweig des Fächers mit der Wurzel 11 zum ersten Mal bereits mit der Zahl 5. Wir wissen bei der Zahl 5 bereits, dass dort eine neue Hüllenlinie beginnen muss, und wir wissen auch, wo (bei welcher negativen Potenz) sie beginnen muss. Denn die äußeren Zweige sämtlicher Fächer gehorchen genauso der Regel des Mindestabstands von 1 zum nächsten Fächer. Fächer dürfen sich also genausowenig berühren wie Äste und müssen gleichzeitig so dicht wie möglich zusammengerückt sein.
|
Bild 79 |
Der äußere Zweig des Fächers Nr. 4 (damit meine ich denjenigen, der seine Wurzel in der Zeile 4 hat), beginnt also bereits in Zeile 2 mit der Potenz −2. Die Länge des Zweiges entspricht genau der Summe der beiden gegenüberliegenden Astglieder auf der Außenseite (Bild 79 grau). |
|
Bild 80 |
In Bild 80 ist das Außenglied des nächsten Fächers zu sehen, gegenüberliegend die seine Länge bestimmenden zwei Glieder des Außenastes. Die Fächerzweige lassen sich also ziemlich einfach als die jeweiligen Summen der beiden genau gegenüberliegenden Astglieder bestimmen. |
Das gilt auch für alle weiter innen liegenden Fächerzweige. Gezeigt werden soll dies anhand von Bild 81, das einen Abschnitt unseres Phi-Musters von Zeile 29 bis Zeile 77 zeigt.
|
Bild 81 |
Auf diese Weise können wir also alle Zweige bestimmen, die in einem Fächer nach oben streben. |» Was ist mit den Zweigen, die nach unten streben? Diese können wir nicht so ohne weiteres auf die gleiche Weise bestimmen. «| Du hast recht. Hier müssen wir ein wenig anders vorgehen. Um das zu demonstrieren, habe ich den Ausschnitt zwischen Zeile 76 und Zeile 123 vorbereitet und dort auf der Außenseite die beiden längeren Astteile und auf der Innenseite den längeren der Fächerzweige, die nach unten weisen, blau markiert (Bild 82). |
|
Bild 82 |
Bild 83 |
Wir sehen sofort, dass die Länge des Fächerzweigs der Differenz-Länge der beiden Ast-Teilstücke entspricht. Um die Länge des nächst-inneren Fächerzweigs bestimmen zu können, müssen wir auch noch die beiden nächsten Ast-Teilstücke von der Länge des äußeren Astteiles abziehen (Bild 83). Wir sehen somit eine grundsätzliche Methode, wie wir die Längen sämtlicher Äste und Zweige bestimmen können, ohne irgendwelche Zahlen zum Abzählen zu Hilfe nehmen zu müssen. |
Ich überlasse es dem Leser, weitere »Arten« dieser Zusammenhänge herauszufinden – es gibt deren noch etliche! Zusammenfassend können wir sagen, dass die Summe der einzelnen Punkte auf der Innenseite stets der Summe der Punkte auf der Außenseite entspricht – mit der Einschränkung, dass wir jeweils am Ende eines Astteiles des Außenastes messen, d.h. innerhalb des Längenbereiches eines Teilastes kann der Wert schwanken, er gleicht sich am Ende des Teilstücks aber immer wieder genau aus. Wir wollen diese Behauptung, die uns nun wieder in die »Welt des Zählens und der Zahlen« führt, überprüfen.
|» Bevor wir in jeder Zeile die einzelnen »Potenzpunkte« abzählen, sollten wir uns darauf einigen, welcher Seite wir die Punkte auf der Nulllinie zuschlagen.
«| Ich denke, wir sollten sie beiden Seiten zuschlagen, da wir gesehen haben, dass die Wurzeln auf der Nulllinie sich stets überlappen. (Wir könnten Sie aber genausogut weglassen – es würde keinen Einfluss auf das Ergebnis haben.)
|» Gut, dann erstelle bitte eine Übersichts-Grafik, in welche du die Summe der Punkte für jede Zeile einträgst – getrennt für die Außen- und die Innenseite.
|
Bild 84 |
«| Du bekommst nicht nur das, ich habe in Bild 84 die Abweichungen auch in grafischer Form eingetragen. Dabei habe ich mich auf die Werte für die Zeilen 1 bis 76 beschränkt. Die einzelnen Abschnitte des Außenastes habe ich rechts mit horizontalen, gestrichelten Linien markiert. Links, innerhalb der Zeilennummern, ist die Anzahl der Punkte für die Außenseite eingetragen, unmittelbar rechts von der Grafik die Anzahl der Punkte für der Innenseite. Punkte, die auf der Nulllinie liegen, werden sowohl für die Zählung der Außen- als auch der Innenseite verwendet. Die Zahlenkolonne rechts außen enthält die Differenz zwischen der Anzahl auf der Außen- und der Anzahl auf der Innenseite. Diese Differenzwerte sind in grafischer Form ganz rechts als graue Balken eingezeichnet. Wir sehen somit, dass auf jedem Außenastabschnitt die Differenzwerte symmetrisch angeordnet sind, wobei sich die positiven und die negativen Differenzen jeweils genau ausgleichen. Bild 85 und Bild 86 zeigen drei weitere Abschnitte des Außenastes. Das Prinzip, wie sich die Symmetrie noch weiter fortsetzt, kann man sich gut vorstellen. |

| Bild 85 | Bild 86 |
Symmetrie ist jedenfalls ein wichtiges Kennzeichen unseres gesamten, bis ins Unendliche reichenden Musters.