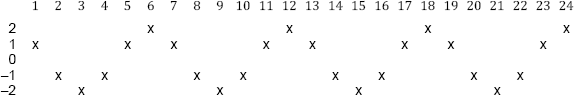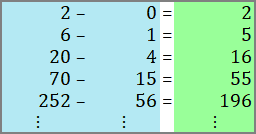Eine Folge und deren Folgen
Die Glieder der Folge 1, 3, 4, 7, 11, 18, 29, ... (auch Lucas-Folge – nach dem französischen Mathematiker Édouard Lucas – genannt) sind die ganzzahligen Teile der (ganzzahligen) Potenzen von Φ. Mit Potenz bezeichnen die Mathematiker die Anzahl, wie oft eine Zahl mit sich selbst multipliziert wird. Wenn ich eine Zahl mit sich selbst multipliziere, dann entspricht das Ergebnis der 2. Potenz dieser Zahl – wir sagen dazu auch: das Quadrat dieser Zahl. Wenn ich beispielsweise das Quadrat von 7 berechne, dann rechne ich 7 ⋅ 7 = 49 oder auch 72 = 49. Die kleine hochgestellte Zahl gibt die Potenz der Zahl 7 an. Man sagt dazu auch »7 zum Quadrat« oder »7 hoch 2«.
Multipliziert man das Ergebnis ein weiteres Mal mit 7, erhält man die 3. Potenz von
7:
7 ⋅ 7 ⋅ 7 = 343 oder auch 73 = 343.
In unserem Fall haben wir die Zahl Φ wiederholt mit sich selbst multipliziert und sind so zu ihren Potenzen gelangt:
| Φ1 | = | 1 | ,6180... |
| Φ2 | = | 2 | ,6180... |
| Φ3 | = | 4 | ,2360... |
| Φ4 | = | 6 | ,8541... |
| Φ5 | = | 11 | ,0901... |
| Φ6 | = | 17 | ,9442... |
| Φ7 | = | 29 | ,0344... |
| Φ8 | = | 46 | ,9787... |
| ⋮ | |||
Beim Betrachten der Folge, deren Glieder alle »gerundete« Potenzen von Φ sind, ist mir Folgendes aufgefallen:
| Φ1 | = | 1 | |
| Φ2 | = | 3 | |
| Φ3 | = | 4 | |
| Φ4 | = | 7 | |
| Φ5 | = | 11 | |
| Φ6 | = | 18 | |
| Φ7 | = | 29 | |
| Φ8 | = | 47 | |
| ⋮ | |||
Alle geraden Potenzen (also die Potenzzahlen 2, 4, 6, 8, ...) sind Zahlen, die von »echten Quadratzahlen« um genau 2 abweichen:
| Φ2 | = | 3 | Φ2 | = | (Φ1)2 + 2 = | 12 + 2 = | 1 + 2 = | 3 | |
| Φ4 | = | 7 | Φ4 | = | (Φ2)2 − 2 = | 32 − 2 = | 9 − 2 = | 7 | |
| Φ6 | = | 18 | Φ6 | = | (Φ3)2 + 2 = | 42 + 2 = | 16 + 2 = | 18 | |
| Φ8 | = | 47 | Φ8 | = | (Φ4)2 − 2 = | 72 − 2 = | 49 − 2 = | 47 | |
| Φ10 | = | 123 | Φ10 | = | (Φ5)2 + 2 = | 112 + 2 = | 121 + 2 = | 123 | |
| Φ12 | = | 322 | Φ12 | = | (Φ6)2 − 2 = | 182 − 2 = | 324 − 2 = | 322 | |
| Φ14 | = | 843 | Φ14 | = | (Φ7)2 + 2 = | 292 + 2 = | 841 + 2 = | 843 | |
| ⋮ | ⋮ |
Und zwar weichen sie immer abwechselnd um +2 oder −2 ab. Die »Schwankung um den Idealwert« ist also immer gleich groß, einmal um 2 darüber, dann wieder um 2 darunter, usw. Gemessen an der Größe der Zahl wird die Abweichung aber natürlich immer kleiner. Bei 7 fällt eine Abweichung von 2 viel mehr ins Gewicht als bei 843, und bei einer so großen Zahl wie Φ40 = 228.826.127 wird sie geradezu winzig. Dennoch »schwingt die Oberfläche mit einer Amplitude von ±2«.
Dieses Verhalten, dass hier immer eine Abweichung von genau 2 vorliegt, schien mir ziemlich auffällig. Ich schaute mir daher zunächst die ungeraden Potenzen näher an:
| Φ1 | = | 1 | |
| Φ3 | = | 4 | |
| Φ5 | = | 11 | |
| Φ7 | = | 29 | |
| Φ9 | = | 76 | |
| Φ11 | = | 199 | |
| Φ13 | = | 521 | |
| ⋮ | |||
Da war nichts zu sehen ... keine irgendwelchen Quadratzahlen ähnlichen Zahlen. Ich suchte also weiter und nahm mir die Potenzen, die sich durch 3 teilen lassen, vor:
| Φ3 | = | 4 | |
| Φ6 | = | 18 | |
| Φ9 | = | 76 | |
| Φ12 | = | 322 | |
| Φ15 | = | 1364 | |
| Φ18 | = | 5778 | |
| Φ21 | = | 24476 | |
| ⋮ | |||
Vielleicht würde sich eventuell bei den 3. Potenzen eine Gesetzmäßigkeit erkennen lassen – und siehe da:
| (Φ2)3 | = Φ6 | = | 18 = | 33 − | 9 |
| (Φ3)3 | = Φ9 | = | 76 = | 43 + | 12 |
| (Φ4)3 | = Φ12 | = | 322 = | 73 − | 21 |
| (Φ5)3 | = Φ15 | = | 1.364 = | 113 + | 33 |
| (Φ6)3 | = Φ18 | = | 5.778 = | 183 − | 54 |
| (Φ7)3 | = Φ21 | = | 24.476 = | 293 + | 87 |
| (Φ8)3 | = Φ24 | = | 103.682 = | 473 − | 141 |
| ⋮ | ⋮ | ||||
Ich gebe zu, das hat etwas mehr als nur ein paar Minuten gedauert, bis ich diese Gesetzmäßigkeit herausgefunden hatte. Aber dass es sich hier um eine Gesetzmäßigkeit handelt, ist für ein geübtes Auge sofort erkennbar.
Auf der rechten Seite der Gleichung steht immer ein Wert aus unserer Folge und dazu eine Differenz. Diese Differenz ist jetzt nicht wie bei der quadratischen Tabelle immer genau 2, sondern steigt jeweils leicht an (leicht in Bezug auf den Ergebniswert). Ich erläutere die Werte etwas genauer am Beispiel der 4. Zeile:
(Φ5)3 = Φ15 = 1364 = 113 + 33
Φ5 ist das 5. Glied unserer Folge, also 11. Dieses erhebe ich zur 3. Potenz. Das ergibt dann die 15. Potenz von Φ. (Ich muss Φ zuerst 5-mal mit sich selbst multiplizieren, dadurch erhalte ich die 5. Potenz, und das muss ich insgesamt 3-mal machen, also 5 ⋅ 3-mal, das entspricht der 15. Potenz).
Die Abweichung zwischen Φ15 = 1364 und 113 = 1331 beträgt 33. Den Wert der Abweichung kann ich auch so schreiben:
33 = 3⋅11
Schwant dir schon etwas? Schau dir die Zahlen der Abweichungen an:
| 9 = | 3⋅3 |
| 12 = | 4⋅3 |
| 21 = | 7⋅3 |
| 33 = | 11⋅3 |
| 54 = | 18⋅3 |
| 87 = | 29⋅3 |
| 141 = | 47⋅3 |
«| Interessant!! Da will ich mir doch auch gleich mal jede 5. Potenz anschauen. Warum ausgerechnet jede 5. Potenz und nicht erst mal jede 4. Potenz? Weil ich die jeweils 4. Potenzen bereits kenne (sie sind ein Teil der jeweils 2. Potenzen ...). Also:
| (Φ2)5 | = Φ10 | = | 123 = | 35 − | 120 |
| (Φ3)5 | = Φ15 | = | 1.364 = | 45 + | 340 |
| (Φ4)5 | = Φ20 | = | 15.127 = | 75 − | 1.680 |
| (Φ5)5 | = Φ25 | = | 167.761 = | 115 + | 6.710 |
| (Φ6)5 | = Φ30 | = | 1.860.498 = | 185 − | 29.070 |
| (Φ7)5 | = Φ35 | = | 20.633.239 = | 295 + | 122.090 |
| ⋮ | ⋮ | ||||
Hmmm ... Die Differenzwerte wachsen jetzt aber ganz schön schnell! Da blicke ich noch nicht durch. Vielleicht sollte ich es doch vorher mit den jeweils 4. Potenzen versuchen ...
| (Φ2)4 | = Φ8 | = | 47 = | 34 − | 34 |
| (Φ3)4 | = Φ12 | = | 322 = | 44 + | 66 |
| (Φ4)4 | = Φ16 | = | 2.207 = | 74 − | 194 |
| (Φ5)4 | = Φ20 | = | 15.127 = | 114 + | 486 |
| (Φ6)4 | = Φ24 | = | 103.682 = | 184 − | 1.294 |
| (Φ7)4 | = Φ28 | = | 710.647 = | 294 + | 3.366 |
| ⋮ | ⋮ | ||||
Schon besser. Aber von einem linearen Anwachsen der Differenzwerte keine Spur. Eher schon ein quadratisches Anwachsen. Ja! Überprüfen wir doch, ob sich da quadratische Werte verstecken ... Wie wär’s, wenn wir die jeweilige Basiszahl zum Quadrat nehmen? In der 2. Reihe hieße der Wert 42, in der 3. Reihe 72. Nö, das kann nicht passen, das weicht zu viel von den tatsächlichen Differenzwerten ab. Eventuell ist ein Faktor dabei im Spiel, z. B. 4 (bei den 3. Potenzen war der Faktor 3 im Spiel, hier könnte es 4 sein ...). Also ausprobieren:
| (Φ2)4 | = Φ8 | = | 47 = | 34 − | 4⋅ | 32 + 2 |
| (Φ3)4 | = Φ12 | = | 322 = | 44 + | 4⋅ | 42 + 2 |
| (Φ4)4 | = Φ16 | = | 2.207 = | 74 − | 4⋅ | 72 + 2 |
| (Φ5)4 | = Φ20 | = | 15.127 = | 114 + | 4⋅ | 112 + 2 |
| (Φ6)4 | = Φ24 | = | 103.682 = | 184 − | 4⋅ | 182 + 2 |
| (Φ7)4 | = Φ28 | = | 710.647 = | 294 + | 4⋅ | 292 + 2 |
| ⋮ | ⋮ | |||||
Stimmt!! Das war gar nicht so schwer. Ob man die quadratischen Glieder positiv oder negativ nehmen soll, das sieht man ohnehin sofort, sobald man das erste Glied mit der 4. Potenz ausgerechnet hat. Und dann passt alles bereits bis auf den Rest 2. Dieser Wert 2 ist immer gleich, während das Vorzeichen bei den quadratischen Werten abwechselnd + und – ist.
Jetzt also nochmal zu den 5. Potenzen. Es wäre doch gelacht, wenn es mir nicht auch dort gelingen würde, das Bildungsgesetz herauszufinden:
| (Φ2)5 | = Φ10 | = | 123 = | 35 − | 5⋅ | 33 + 5⋅ | 3 |
| (Φ3)5 | = Φ15 | = | 1.364 = | 45 + | 5⋅ | 43 + 5⋅ | 4 |
| (Φ4)5 | = Φ20 | = | 15.127 = | 75 − | 5⋅ | 73 + 5⋅ | 7 |
| (Φ5)5 | = Φ25 | = | 167.761 = | 115 + | 5⋅ | 113 + 5⋅ | 11 |
| (Φ6)5 | = Φ30 | = | 1.860.498 = | 185 − | 5⋅ | 183 + 5⋅ | 18 |
| (Φ7)5 | = Φ35 | = | 20.633.239 = | 295 + | 5⋅ | 293 + 5⋅ | 29 |
| ⋮ | ⋮ | ||||||
Voilà!! Bitte nachrechnen!
Ganz unter uns: Ich habe das nicht einfach so hingeschrieben, da musste ich ganz schön viel herumprobieren, bis alles gepasst hat. Aber nachdem die ersten 3 Werte zu einem richtigen Ergebnis führten, ich also auf der richtigen Spur war, klappte es auch bei allen anderen. Ich hatte das Bildungsgesetz gefunden!
Nun, das hat jetzt richtig Spaß gemacht – machen wir gleich weiter bei den jeweils 6. Potenzen:
| (Φ2)6 | = Φ12 | = | 322 = | 36 − | 6⋅ | 34 + 9⋅ | 32 − 2 |
| (Φ3)6 | = Φ18 | = | 5.778 = | 46 + | 6⋅ | 44 + 9⋅ | 42 + 2 |
| (Φ4)6 | = Φ24 | = | 103.682 = | 76 − | 6⋅ | 74 + 9⋅ | 72 − 2 |
| (Φ5)6 | = Φ30 | = | 1.860.498 = | 116 + | 6⋅ | 114 + 9⋅ | 112 + 2 |
| (Φ6)6 | = Φ36 | = | 33.385.282 = | 186 − | 6⋅ | 184 + 9⋅ | 182 − 2 |
| (Φ7)6 | = Φ42 | = | 599.074.578 = | 296 + | 6⋅ | 294 + 9⋅ | 292 + 2 |
| ⋮ | ⋮ | ||||||
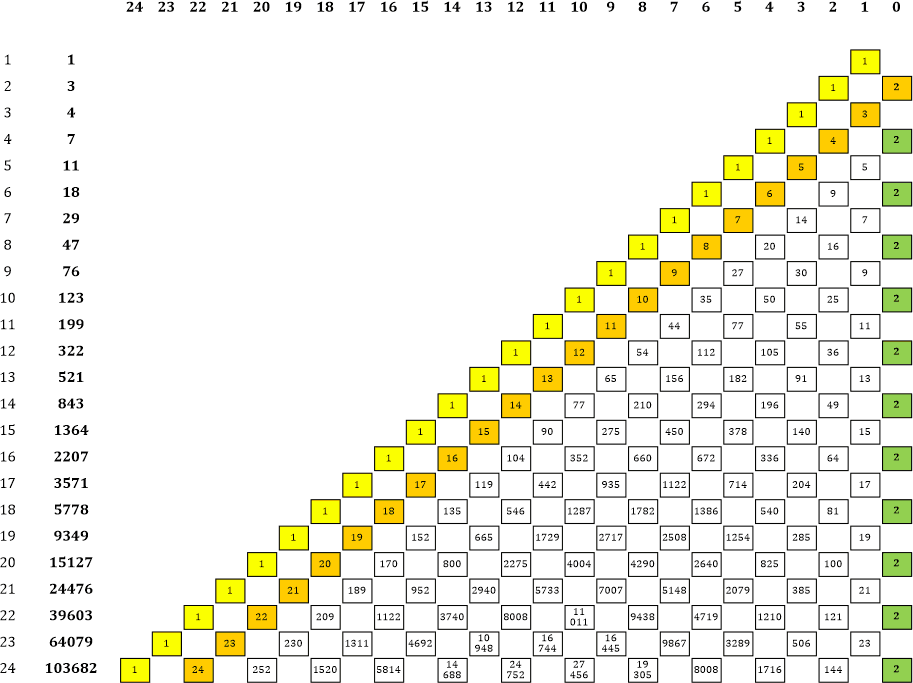
Woher der Faktor 9 bei den quadratischen Gliedern kommt ...?? Dazu habe ich vorläufig keine Ahnung. Ich werde jetzt erstmal etwas Systematik in diese Sache hineinbringen und schreibe die Faktoren in eine Tabelle:
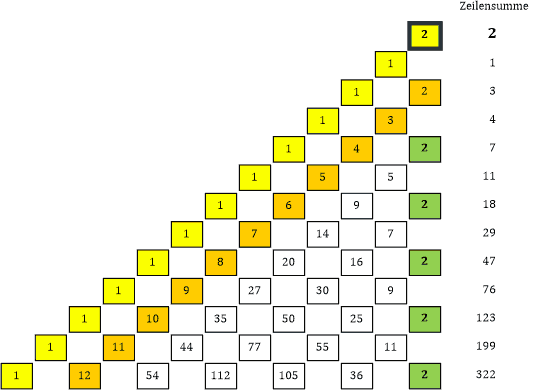
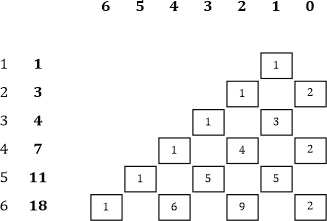 Tabelle 1 |
Die Spaltenüberschriften stellen die Potenzen dar, die Ziffern in der ganz linken Spalte die Potenzen p für Φ und die fettgedruckten Zahlen daneben jeweils den ganzzahligen Teil von Φp. Sieht gut aus! Ein paar Dinge kann man auf einen Blick erkennen: |
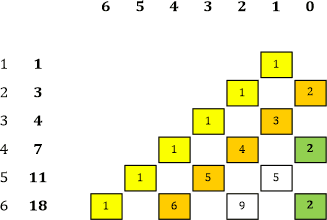 Tabelle 2 |
Die gelbe Linie ist klar, sie setzt sich immer mit dem Wert 1 nach links unten fort. Die orange Linie entspricht den Natürlichen Zahlen (beginnend bei 2). Die vertikale grüne Linie scheint sich nach unten mit dem konstanten Wert 2 immer in jeder 2. Zeile fortzusetzen. |
Bleiben noch die beiden Werte 5 und 9 auf weißem Hintergrund. Hier kann ich auf den ersten Blick keine Gesetzmäßigkeit erkennen. Oder doch? 5 könnte die Summe aus den beiden Werten darüber sein (5 = 3 + 2), diese Vorgangsweise würde auch zum Wert (9 = 4 + 5) und allen übrigen Werten (z. B. 4 = 1 + 3) passen.
Was mir noch auffällt: Die auf ganze Zahlen gerundeten Potenzen von Φ (1, 3, 4, 7, 11, 18, ...) entsprechen immer genau der Summe aller Faktoren in der jeweiligen Zeile:
| 1 | = 1 |
| 3 | = 1 + 2 |
| 4 | = 1 + 3 |
| 7 | = 1 + 4 + 2 |
| 11 | = 1 + 5 + 5 |
| 18 | = 1 + 6 + 9 + 2 |
| ⋮ | ⋮ |
| ? |
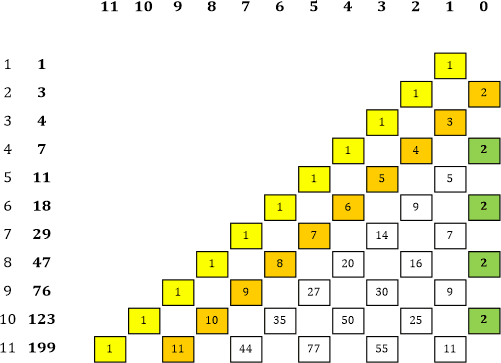 Tabelle 3 |
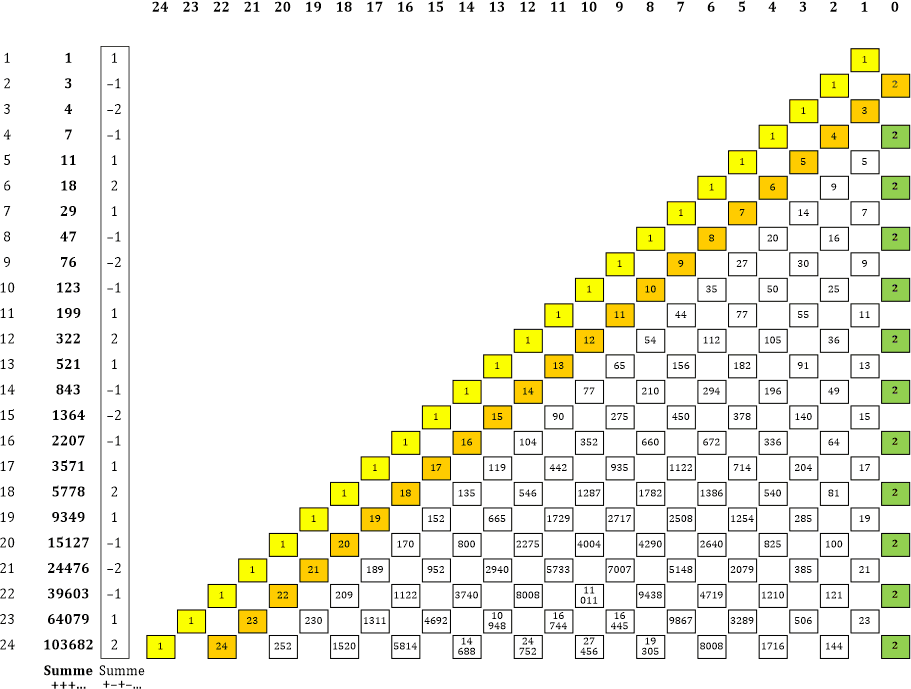
Zunächst die Zeilensummen:
Alles passt! Jetzt muss ich aber auch noch die Potenzsummen überprüfen. Ich beginne mit der 7. Zeile: |
| (Φ2)7 | = Φ14 | = | 843 = | 37 − | 7⋅ | 35 + 14⋅ | 33 − 7⋅ | 3 |
| (Φ3)7 | = Φ21 | = | 24.476 = | 47 + | 7⋅ | 45 + 14⋅ | 43 + 7⋅ | 4 |
| (Φ4)7 | = Φ28 | = | 710.647 = | 77 − | 7⋅ | 75 + 14⋅ | 73 − 7⋅ | 7 |
| (Φ5)7 | = Φ35 | = | 20.633.239 = | 117 + | 7⋅ | 115 + 14⋅ | 113 + 7⋅ | 11 |
| ⋮ | ⋮ | |||||||
Bis hierher stimmt alles. Meine Zuversicht steigt! Weiter mit der 8. Zeile:
| (Φ2)8 | = Φ16 | = | 2.207 = | 38 − | 8⋅ | 36 + 20⋅ | 34 − 16⋅ | 32 + 2 |
| (Φ3)8 | = Φ24 | = | 103.682 = | 48 + | 8⋅ | 46 + 20⋅ | 44 + 16⋅ | 42 + 2 |
| (Φ4)8 | = Φ32 | = | 4.870.847 = | 78 − | 8⋅ | 76 + 20⋅ | 74 − 16⋅ | 72 + 2 |
| (Φ5)8 | = Φ40 | = | 228.826.127 = | 118 + | 8⋅ | 116 + 20⋅ | 114 + 16⋅ | 112 + 2 |
| ⋮ | ⋮ | |||||||
Her mit dem Taschenrechner! ... Alle Werte stimmen! Jetzt traue ich mir schon hohe Wetten abzuschließen, dass auch die Werte in der Zeile 9 stimmen:
| (Φ2)9 | = Φ18 | = | 5.778 = | 39 − | 9⋅ | 37 + 27⋅ | 35 − 30⋅ | 33 + 9⋅ | 3 |
| (Φ3)9 | = Φ27 | = | 439.204 = | 49 + | 9⋅ | 47 + 27⋅ | 45 + 30⋅ | 43 + 9⋅ | 4 |
| (Φ4)9 | = Φ36 | = | 33.385.282 = | 79 − | 9⋅ | 77 + 27⋅ | 75 − 30⋅ | 73 + 9⋅ | 7 |
| (Φ5)9 | = Φ45 | = | 2.537.720.636 = | 119 + | 9⋅ | 117 + 27⋅ | 115 + 30⋅ | 113 + 9⋅ | 11 |
| ⋮ | ⋮ | ||||||||
Ich bin jetzt sicher: Die Gesetzmäßigkeit ist erkannt!
Ich kann daher die Tabelle beliebig erweitern und mit ihrer Hilfe alle Potenzen von Φ auch in Form einer Potenzsumme darstellen.
Ich mache noch einen abschließenden Test mit der 24. Zeile:
| (Φ2)24 | = | Φ48 = 10.749.957.122 = |
| = | 324 − 24⋅322 + 252⋅320 − 1.520⋅318 + 5.814⋅316 − 14.688⋅314 + 24.752⋅312 − | |
| 27.456⋅310 + 19.305⋅38 − 8.008⋅36 + 1.716⋅34 − 144⋅32 + 2 |
Korrekt!
«| Wieso probierst du es nicht auch mal mit (Φ1)24 = Φ24 ?
|» Du hast recht. Ich habe das bloß deshalb bisher nicht gemacht, weil dann die Basen der einzelnen Potenzglieder jeweils 1 sind. Und 1 kann man beliebig oft mit sich selbst multiplizieren, es ändert sich dadurch nichts.
«| Aber es gibt doch auch noch jeweils die Faktoren vor jeder 1 ...
|» Klar! Jetzt sehe ich’s! Das ist nichts Anderes als die jeweilige Zeilensumme der Faktoren! Ich nehme gleich noch mal die 24. Zeile her und rechne das nach:
| (Φ1)24 | = | Φ24 = 103.682 = |
| = | 124 − 24⋅122 + 252⋅120 − 1.520⋅118 + 5.814⋅116 − 14.688⋅114 + 24.752⋅112 − | |
| 27.456⋅110 + 19.305⋅18 − 8.008⋅16 + 1.716⋅14 − 144⋅12 + 2 | ||
| = | 2 |
... hmmm. Das stimmt aber nicht! Da kommt als Ergebnis 2 heraus! Sonderbar ...
«| Ich weiß nicht, ob das falsch ist, aber bei der Berechnung der Zeilensummen hast du nie ein negatives Vorzeichen verwendet. Setz doch mal einfach alle Vorzeichen auf +.
|» Du hast recht. Ich schreibe jetzt auch die Potenzen von 1 nicht mehr hin, da 1 zu irgendeiner Potenz ohnehin immer 1 bleibt. Gib mir mal den Taschenrechner:
| 103.682 | = | 1 + 24 + 252 + 1.520 + 5.814 + 14.688 + 24.752 + 27.456 + 19.305 + 8.008 + |
| 1.716 + 144 + 2 |
Jetzt stimmt die Rechnung. Die Vorzeichen scheinen je nach Basis immer zu wechseln oder gleich zu bleiben.
Dieses Ergebnis 2 bei alternierenden Vorzeichen irritiert mich jetzt aber doch. Ich rechne das mal bei mehreren Zeilen nach. Ich möchte wissen, ob tatsächlich jeweils 2 herauskommt.
«| Berechne doch gleich alle Zeilen. Nimm dafür dein Tabellenkalkulationsprogramm.
|» Ja, mach ich. Ich berechne die Zeilensumme einmal mit lauter positiven Vorzeichen und daneben mit alternierenden Vorzeichen (also immer abwechselnd + und −).
Die »normale« Zeilensumme hatten wir bereits, aber die »alternierende« sieht wirklich interessant aus. Die Werte schwanken zwischen +2 und −2, und das in einem stets gleich bleibenden Rhythmus. Nach 6 Potenzen wiederholt sich alles.
Es erinnert mich an eine Sinuskurve:
«| ... oder eine Schlange, die sich um eine gerade Linie herum vorwärtswindet ...
|» Diese »Schlange« werde ich im Auge behalten ... ich habe es mir soeben notiert. – Sag mal, was hältst du davon, wenn wir uns den Aufbau unserer schönen Tabelle etwas näher ansehen? Vielleicht finden wir noch ein paar besondere Dinge.
«| Gute Idee!
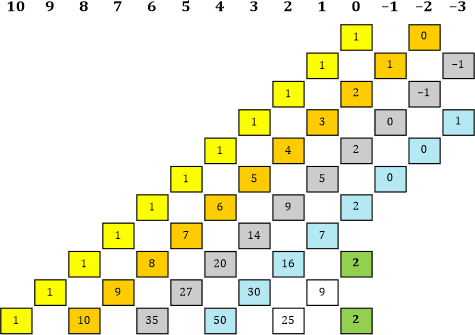
|» Die diversen bunten Linien sind bereits eingezeichnet. Das Nächste, das mir auffällt, ist die Spalte gleich links neben der vertikalen 2er-Linie, sie enthält alle ungeraden Zahlen.
«| Und die Spalte wiederum links davon enthält lauter „Quadratzahlen“!
|» Wie bitte? 1, 4, 9, 16, 25, 36, 49, ... Ah, tatsächlich – lauter Quadrate!
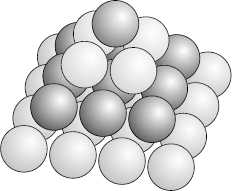 Bild 10 |
|
|||||||||||||||||||
Mir fällt noch etwas auf: Die orange Linie beginnt mit 2 und nicht mit 1. Ich hätte mir erwartet, dass sie mit 0 oder 1 beginnt.
|» Vielleicht gehört ja diese 1 ohnehin dorthin ... und zusätzlich könnte man auch gleich noch die orange Linie weiter nach oben hin verlängern:
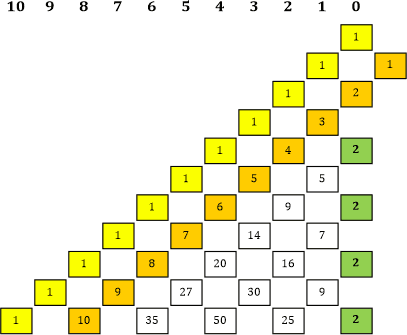 Tabelle 7a |
Das gefällt mir! Auf diese Weise stimmt sogar der Wert der 2 sowohl in der grünen vertikalen Linie (lauter 2er) als auch in der orangen Linie (1, 2, 3, 4, ...). «| Wie meinst du das? |
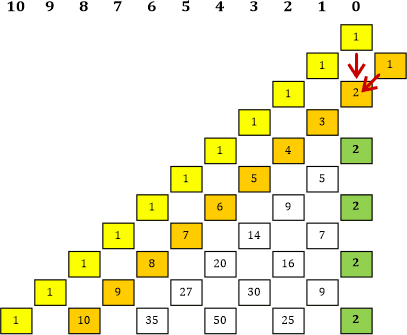 Tabelle 7b |
|» Der erste 2er-Wert ergibt sich dadurch wie bei allen anderen Zahlen in der Tabelle durch Addition der beiden oberhalb (bzw. rechts oberhalb) stehenden Zahlen, nämlich 1 + 1 = 2. «| Und die anderen 2er darunter in der grünen Linie ergeben sich durch Addition von 2 + 0 = 2 ! |
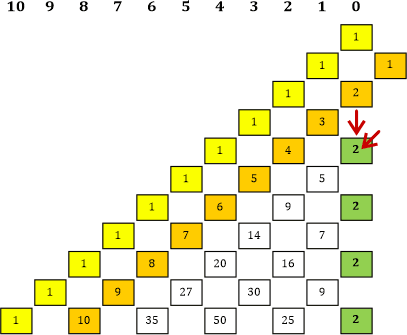 Tabelle 7c |
|» Wenn man »nichts« als 0 interpretiert ... die Idee gefällt mir! «| Weißt du, was mich an unserer ganzen Konstruktion noch stört? Sie enthält lediglich den ganzzahligen Teil der Potenzen von Φ. Meinst du, wir könnten da auch irgendwo die Teile rechts vom Komma herauslesen? |
|» Puh! Du stellst Fragen ... Aber es ist natürlich eine sehr gute Frage ...
Lass mich mal überlegen. Mir fällt auf, dass es in unserer Tabelle eine einzige Zahl gibt, die rechts von der grünen Linie liegt: Im orangen Feld mit der 1. Links davon steht ebenfalls eine 1 und sonst nichts. Die linke 1 liegt unter der Potenz 1, d. h. sie bedeutet Φ1. Und die rechte 1? Die liegt unter keinem Potenzwert.
«| Doch! Verlängere die oberste Zeile, in welcher die fettgedruckten Potenzwerte stehen, weiter nach rechts! Mach es so wie auf einer normalen Zahlengeraden, da geht es »unterhalb« von 0 mit −1, −2, ... etc. weiter. Und dann liegt die orange 1 unterhalb der Potenz −1.
|» Ja, prima!! Das würde sogar stimmen, denn der Wert rechts vom Komma der Zahl Φ entspricht ja tatsächlich ihrem Kehrwert. Kehrwerte – sie werden auch reziproke Werte genannt – schreibt man in der Mathematik auch als »hoch minus 1«. Schreiben wir es auf:
| Φ−1 = |
|
⇒ 0,61803 = |
|
«| Ich mache dir noch einen Vorschlag: Wir haben in der Tabelle bereits zwei schräg laufende Linien (gelb und orange) eingezeichnet. Zeichnen wir probehalber eine weitere parallel dazu verlaufende Linie ein – ich mache sie grau:
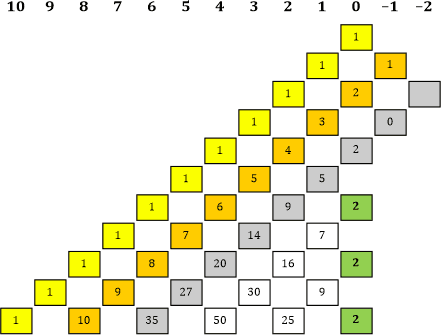 Tabelle 8 |
|» Ah, ich sehe, du hast auch bereits eine 0 in der grauen Linie eingezeichnet! Wir hatten ja vorhin
gesagt, dass rechts von der »2er-Spalte« lauter Nullen sein müssten. Aber passt das auch zu der grauen
Linie? Sehen wir uns doch den »Verlauf« der grauen Linie von links unten nach rechts oben an: |
| 35 | − | 8 | = | 27 |
| 27 | − | 7 | = | 20 |
| 20 | − | 6 | = | 14 |
| 14 | − | 5 | = | 9 |
| 9 | − | 4 | = | 5 |
| 5 | − | 3 | = | 2 |
| 2 | − | 2 | = | 0 |
| 0 | − | 1 | = | −1 |
«| Heehh! Halt, stopp! Was machst du denn da?
|» Wieso?
«| Na, du bist über die 0 hinausgegangen ...
|» Das stimmt nur zum Teil. Ich habe von den Werten einen fortlaufend um 1 geringeren Betrag abgezogen, und zwar so lange, bis dieser abzuziehende Betrag 1 war. Schau auf die fettgedruckten Werte in der Mitte der Auflistung! (8 7 6 5 4 3 2 1)
«| Ah! Ja gut, dann haben wir jetzt auch einen Wert für das bisher leer gebliebene graue Feld, nämlich –1. Das ist auch wirklich passend, denn dadurch ergibt sich für die graue 0 sogar eine richtige Addition (nach der gleichen Vorgangsweise wie bei den anderen Zahlen):
1 + (−1) = 0
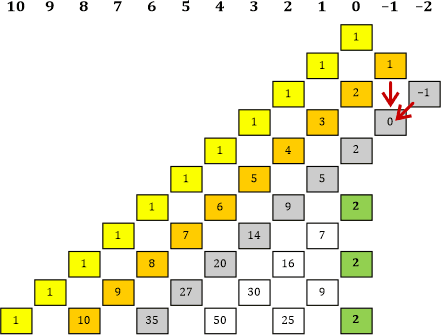
Tabelle 9
|» Mhm. Der Wert −1 ist zwar eigenartig, aber ich denke, über die Vorzeichen sollten wir uns vorerst nicht allzuviele Gedanken machen, denn auf der »linken« Seite der Tabelle sind sie ja ebenfalls manchmal alternierend, obwohl in unserer Tabelle ausschließlich positive Werte eingetragen sind.
Ich möchte jetzt bei den nichtganzzahligen Teilen der Potenzen von Φ weitermachen. Sie entsprechen immer dem Kehrwert der jeweiligen Potenz von Φ, also
|
= Φ−1 = |
|
= 0,61803 | ||||||
|
= Φ−2 = |
|
= 0,38197 | ||||||
|
= Φ−3 = |
|
= 0,23607 | ||||||
|
= Φ−4 = |
|
= 0,14590 | ||||||
|
= Φ−5 = |
|
= 0,09017 | ||||||
| ⋮ | |||||||||
Auf der linken Seite der Tabelle haben wir aber nie mit dem konkreten Wert der Potenzen von Φ gearbeitet, sondern immer mit den gerundeten ganzzahligen Werten. Wir haben also 4 statt 4,23607 verwendet, 7 statt 6,85410, 11 statt 11,09017 usw. Können wir so etwas auch mit den nichtganzzahligen Teilen machen? Wie wäre es, wenn wir jeweils den Kehrwert dieser »gerundeten« ganzzahligen Werte von Φ nehmen?
| 1 ⇒ |
|
= 1 | |||
| 3 ⇒ |
|
= 0,33333 | |||
| 4 ⇒ |
|
= 0,25 | |||
| 7 ⇒ |
|
= 0,14286 | |||
| 11 ⇒ |
|
= 0,09091 | |||
| 18 ⇒ |
|
= 0,05556 | |||
| 29 ⇒ |
|
= 0,03448 | |||
| ⋮ |
«| Das entspricht annähernd den tatsächlichen Werten. Je größer die Werte werden, desto genauer sind die Ergebnisse.
|» Das war zu erwarten. Wie sieht es mit den höheren Potenzen aus? In unserer Tabelle setzen sich die höheren Potenzen aus Potenzsummen zusammen, die immer nur Glieder mit geraden oder ungeraden Potenzen enthalten. Also z. B.
| ⋮ | ||||||||||
| Φ9 | = | 76 = | 19 | + | 9⋅ | 17 + 27⋅ | 15 + 30⋅ | 13 + | 9⋅ | 11 |
| Φ10 | = | 123 = | 110 | + | 10⋅ | 18 + 35⋅ | 16 + 50⋅ | 14 + | 25⋅ | 12 + 2 |
| ⋮ |
Eventuell ist das auch bei den negativen Potenzen so. Vielleicht gibt uns unsere Tabelle einen brauchbaren Hinweis. In der ganz oberen Zeile haben wir die Potenzen eingetragen – rechts von der vertikalen 2er-Linie werden diese negativ. Eventuell setzt sich die Tabelle dorthin noch fort. Bei der grauen Linie haben wir immerhin den Wert −1 unterhalb der Potenz −2 gefunden. Das ist schon mal ein Anfang. Wie könnte denn ein Wert unterhalb der Potenz −3 aussehen?
Wir hatten die Werte der grauen Linie erhalten, indem wir (ich beginne bei 9 in der Spalte mit der Potenz 2) den zwei Zeilen genau darüberliegenden Wert 4 abzogen, dann bei 5 den wieder zwei Zeilen genau darüberliegenden Wert 3 abzogen, bei 2 haben wir 2 abgezogen und 0 erhalten, dort haben wir dann 1 abgezogen und −1 erhalten und jetzt ... ziehen wir 0 ab und erhalten wieder −1. Ich sage das jetzt einfach mal so, denn der zwei Zeilen oberhalb der −1 liegende Wert könnte 0 sein.
|
«| Wie kommst du darauf? » Ich habe die orange Linie um einen Wert verlängert – und der scheint 0 zu sein: |
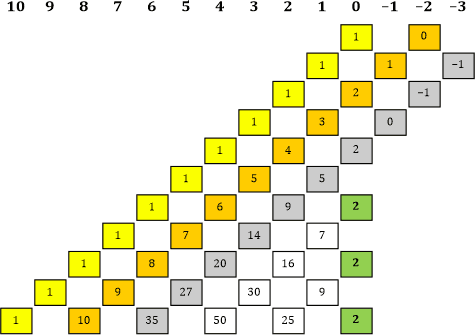 Tabelle 10 |
«| Mach bitte Folgendes: Leg neben die graue Linie noch eine weitere parallele Linie hin ...
|» Meinst du hier? Ich habe sie blau gemacht (Tabelle 11).
Ich erhalte in der Spalte mit der Potenz −3 die Zahl 1.
Lass mich ein wenig überlegen ... Links haben wir immer die Faktoren zu den jeweiligen Potenzen aufgetragen, diese dann zeilenweise zusammengezählt und Φ zur jeweiligen Potenz erhoben erhalten. Also z. B.
| 4 = 13 + 3⋅11 |
| 7 = 14 + 4⋅12 + 2⋅10 |
Rechts müssten dann lauter Werte auftreten, die kleiner als 1 sind – also lauter Brüche. Wenn ich den Kehrwert von beispielsweise Φ6 nehme, ... sei bitte still, ich denke nach ...
| Φ6 | = | 17,94427 | |||||||||
| Φ−6 | = |
|
= |
|
= 0,05577281 | ||||||
Wenn ich immer den ganzzahligen Teil der Potenzen von Φ nehme ...
|
= 0,0555555... |
... dann fehlt noch ein kleines bisschen auf den Wert 0,0557281. Wieviel ist denn das? Rechne das bitte aus.
«| Das ist 0,0557281 − 0,0555555 = 0,0001726.
|» Und jetzt nimm bitte den Kehrwert dieser Zahl.
| «| Dieser ist |
|
= 5.793,7428 . |
|» Kommt dir diese Zahl bekannt vor?
«| Nein ... Moment, warte, ... sie liegt sehr nahe bei Φ18 = 5.778. Wir sind vom Kehrwert von
| Φ−6 | = |
|
≈ |
|
ausgegangen. Und 18 ist 3⋅6 ...
|» Du bringst mich auf eine Idee. Rechnen wir das mal für die größere Zahl auf wesentlich mehr Stellen genau aus.
Φ18 = 5.777,9998269297282877606523800008
Ich probiere jetzt aus, welches Ergebnis ich erhalte, wenn ich vom ganzzahligen Wert 5.778 dessen Kehrwert abziehe:
| 5.778 − |
|
= | 5.777,9998269297334717895465559017 |
Dacht’ ich mir’s doch! Dieser Wert liegt sehr nahe am richtigen Wert! Und zwar liegt er ganz knapp darüber. Und jetzt ziehen wir auch noch den Kehrwert der 3. Potenz von 5.778 ab:
| 5.778 − |
|
− |
|
= | 5.777,9998269297282877609629377287 |
«| Huiii! Eine Genauigkeit von 18 Stellen nach dem Komma!! Wie bist du denn auf diese Idee gekommen?
|» Schau dir unsere Tabelle 11 an: Da steht in der Zeile mit der Potenz 1 links von der vertikalen 2er-Spalte unterhalb der Potenz 1 eine 1 und rechts davon ebenfalls (die orange 1). Aber unter der Spalte mit der Potenz −3 steht nochmal eine 1 (mit negativem Vorzeichen, aber die Vorzeichen können sich ja ändern, wie wir auf der linken Seite bereits gesehen haben). Diese 1 in der Spalte mit der Potenz −3 ist der Grund, warum ich 5.778 auch noch mit der Potenz −3 abgezogen habe! Probieren wir es auch noch mit der Potenz −5 ... vielleicht klappt es ja!
| 5.778 − |
|
− |
|
− |
|
= | 5.777,9998269297282877609629377287 |
«| Das hat nicht funktioniert, die Genauigkeit ist um keine einzige weitere Stelle gewachsen ...
|» Mein Gefühl sagt mir aber, dass ich auf der richtigen Spur bin ... probier es bei der 5. Potenz mit einem Faktor – der Faktor 2 könnte schätzungsweise passen.
| 5.778 − |
|
− |
|
− |
|
= | 5.777,9998269297282877606523800241 |
«| Und wie er passt! Die Übereinstimmung ist bereits bis zur 25. Stelle nach dem Komma angewachsen! Das ist bestimmt kein Zufall.
|» Hoffen wir’s! Aber ich habe nun auf alle Fälle einen neuen Wert für unsere Tabelle! Nämlich eine 2 unterhalb der Spalte mit der Potenz −5.
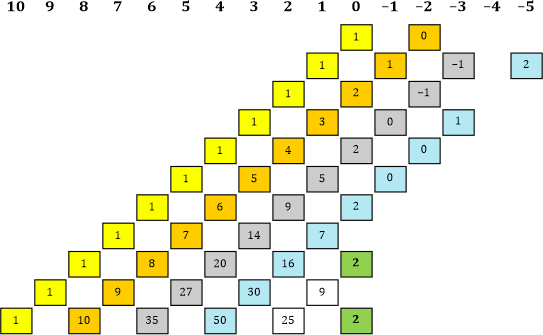
Tabelle 12
Bevor ich an der Tabelle weitertüftle, möchte ich die Rechnung auch noch für eine andere Potenz von Φ überprüfen – sicher ist sicher! Ich nehme einen kleineren Wert: Φ10 – Rechne das bitte nach!
«| O. k.
| Φ10 | = | 122,99186938124421665125227589011 | ||||||||||||||
| 123 − |
|
= | 122,99186991869918699186991869919 | |||||||||||||
| 123 − |
|
− |
|
= | 122,99186938131526863553386674061 | |||||||||||
| 123 − |
|
− |
|
− |
|
= | 122,99186938124422839250969646472 |
|» Die Übereinstimmung wächst diesmal etwas weniger schnell, reicht aber immerhin bereits bis zur 13. Stelle nach dem Komma. Prima!
Ich würde gerne alles mit einem noch kleineren Potenzwert von Φ überprüfen. Voraussichtlich wird die Genauigkeit dann noch weiter abnehmen, aber das Prinzip müsste trotzdem stimmen ...
«| Nehmen wir Φ5?
|» Ja, du kannst schon zu rechnen beginnen.
| Φ5 = 11,090169943749474241022934171828 | ||||||
| 11 − |
|
= | 10,909090909090909090909090909091 | |||
«| Da stimmt etwas nicht ... ah, ich hab’s! Wir haben diesmal eine ungerade Potenz von Φ genommen und diese liegt knapp über dem ganzzahligen Wert, ich muss also wohl den Kehrwert von 11 addieren anstatt ihn abzuziehen.
| 11 + |
|
= | 11,090909090909090909090909090909 |
Das kommt schon eher hin!
| 11 + |
|
+ |
|
= | 11,091660405709992486851990984222 |
Da stimmt aber schon wieder etwas nicht ... der Wert ist zu groß. Ich probiere es besser mit einem negativen Vorzeichen beim letzten Term.
| 11 + |
|
− |
|
= | 11,090157776108189331329827197596 |
|» Die Genauigkeit ist jetzt angestiegen. Die Vorzeichen alternieren vermutlich!
| 11 + |
|
− |
|
+ |
|
= | 11,09017019453465051443331615451 |
«| Sehr gut, wir liegen nun wieder knapp über dem Idealwert, und das ist gut so, denn der nächste Term hat wieder ein negatives Vorzeichen. Fragt sich nur, wie groß er ist ...
|» Probier einfach so lange, bis der nächste Wert wieder unterhalb des Idealwertes liegt. Die Potenz muss auf alle Fälle −7 sein. Du darfst nur den Faktor variieren!
«| In Ordnung. Ich beginne auf gut Glück mit dem Faktor 3.
| 11 + |
|
− |
|
+ |
|
− |
|
= | 11,090170040587215045221289431904 |
Das war noch zu wenig, ich brauche einen etwas größeren Faktor – ich nehme 4.
| 11 + |
|
− |
|
+ |
|
− |
|
= | 11,090169989271403222150613857702 |
Immer noch nicht genug – ich erhöhe auf 5. Das ist fast wie im Casino ...
| 11 + |
|
− |
|
+ |
|
− |
|
= | 11,090169937955591399079938283499 |
|» Jaaa, das schaut gut aus, jetzt liegst du ganz knapp darunter. Mir scheint das eine geeignete Methode zu sein, um noch ein paar weitere Werte zu finden. Ein Mathematiker würde wohl die Nase rümpfen, wenn er uns hier zusehen könnte, ab das ist mir wurscht. Leg los!
«| Der nächste Term muss wieder ein positives Vorzeichen haben und der Faktor wächst vermutlich wieder etwas an. Ich probier’s mit dem Faktor 10.
| 11 + |
|
− |
|
+ |
|
− |
|
+ |
|
= | 11,090169942196567582804787504508 |
Mhm. Zu groß war der Faktor jedenfalls nicht, wir liegen noch knapp unterhalb des Idealwerts. Ich erhöhe auf ... was ist?
|» Lass dich nicht stören, ich mach uns inzwischen einen Kaffee, während du rechnest.
~~~ ~~~ Es duftet nach Kaffee! ~~~ ~~~
Hast du den nächsten Faktor gefunden?
«| Ja, er ist 14! Schau:
| 11 + |
|
− |
|
+ |
|
− |
|
+ |
|
= | 11,090169943892958056294727192911 |
|» Prima, dann werden wir jetzt unsere Tabelle etwas erweitern!
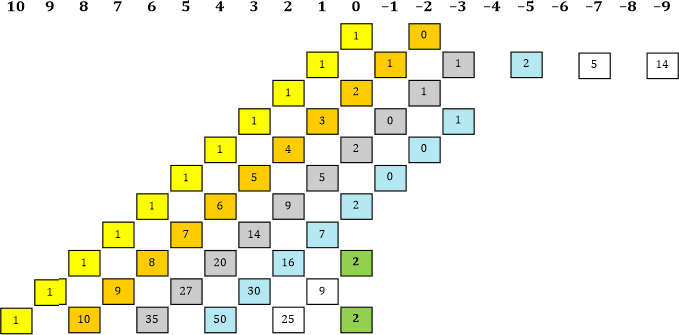
Tabelle 13
«| Ich bin schon gespannt auf den fehlenden Faktor in der blauen Linie (unterhalb der Potenz −4).
|» Du sprichst mir aus der Seele! Hast du eine Idee, welcher Wert da hingehört?
«| Ich tippe auf 1 oder 2. Alle anderen Werte schließe ich aus.
|» Deine Annahme klingt schlüssig. Probieren wir es zunächst mit 1.
«| Ich nehme wieder Φ5, das kenne ich schon so gut.
|» Achtung, diesmal bewegen wir uns aber eine Zeile unterhalb, du musst also die Potenzen alle mit 2 multiplizieren!
«| Verstanden. Ich wähle ab sofort die Schreibweise ohne Brüche, also mit negativen Potenzen statt der Brüche.
| Φ10 = 122,99186938124421665125227589011 | ||||
| (Φ5)2 | = | 112 + 2 − 11−2 + 11−4 | = | 122,99180383853561915169728843658 |
|» Knapp darunter. Nimm den Faktor 2 beim letzten Term.
| (Φ5)2 | = | 112 + 2 − 11−2 + 2⋅11−4 | = | 122,99187213988115565876647769961 |
Wunderbar! Rechne bitte noch zwei weitere Faktoren aus.
«| Bitte schön:
~~~ ~~~ Es dauert ein paar Minuten, bis das Ergebnis auf dem Papier ist ~~~ ~~~
| (Φ5)2 | = | 112 + 2 − 11−2 + 2⋅11−4 − 5⋅11−6 + 14⋅11−8 = |
| = | 122,99186938282253861924199912202 |
Fällt dir etwas auf?
|» Na klar, das sind die gleichen Faktoren wie eine Zeile darüber ... Anscheinend ist hier ein anderes Bildungsgesetz im Spiel als auf der linken Seite. Überprüfen wir das auch noch eine Zeile darunter, du kannst gerne wieder als Ausgangszahl Φ5 nehmen.
«| Mach ich. Aber vorher trage ich noch die neu errechneten Faktoren in unsere Tabelle ein.
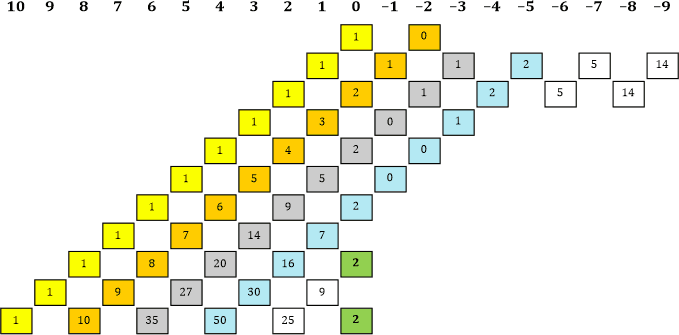
Tabelle 14
| Φ15 | = | 1.364,000733137435857404797968963 | ||
| (Φ5)3 | = | 113 + 3⋅111 − 0⋅11−1 + 1⋅11−3 | = | 1.364,00075131480090 |
Das ist jetzt mal der Wert mit den bekannten Faktoren. Ich probiere es wieder mit dem Faktor 2. Den Term mit dem Faktor 0 lasse ich weg, da er keinen Einfluss auf das Ergebnis hat.
| (Φ5)3 | = | 113 + 3⋅111 + 1⋅11−3 − 2⋅11−5 | = | 1.364,00073889637444 |
|» Dieser Faktor ist anscheinend falsch. Er ist zu klein, wir liegen noch über dem richtigen Wert!
«| Hmm. Du hast recht. Ich probier’s mit 3.
| (Φ5)3 | = | 113 + 3⋅111 + 1⋅11−3 − 3⋅11−5 | = | 1.364,00073268716121 |
|» Treffer! Nächster Wert bitte!
«| Welchen Faktor schlägst du für den ersten Versuch vor?
|» Nimm einfach wieder die 5. Ich räum inzwischen die Küche auf.
~~~ ~~~ Geschirrklappern und leise Musik im Hintergrund ~~~ ~~~
Wie sieht’s aus?
«| Eigenartig. Schau her:
| (Φ5)3 | = | 113 + 3⋅111 + 1⋅11−3 − 3⋅11−5 + 9⋅11−7 − 28⋅11−9 = |
| = | 1.364,0007331371287828963123508 |
|» Aha. Trag doch bitte die gewonnenen Werte in die Tabelle ein.
«| Schon geschehen:
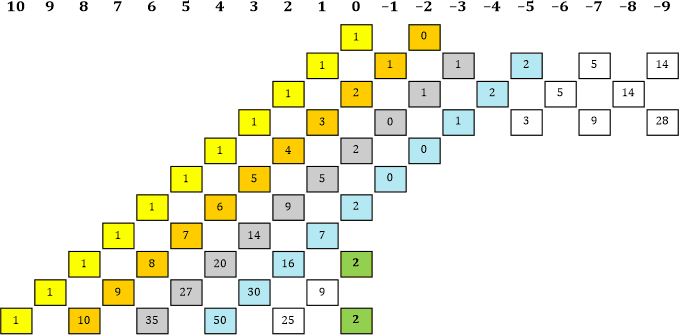
Tabelle 15
|» Naja, ganz so eigenartig ist das gar nicht. Ich erkenne hier gleich mehrere Muster ... am besten hinterlege ich sie farbig, dann sind sie leichter erkennbar:
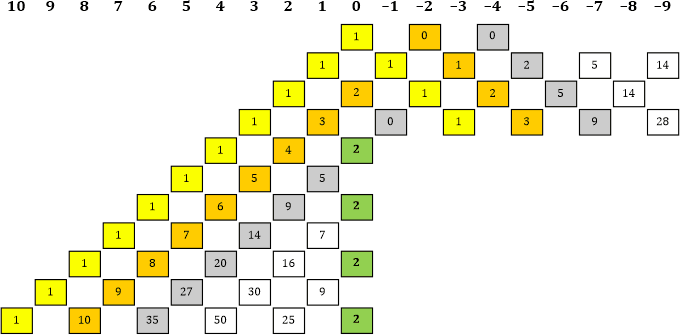
Tabelle 16
«| Aha, du meinst, das setzt sich nach rechts unten genauso fort wie auf der linken Seite? Das möchte ich unbedingt ausprobieren. Ich verlängere die neuen grauen Linien nach rechts unten (Tabelle 17a).
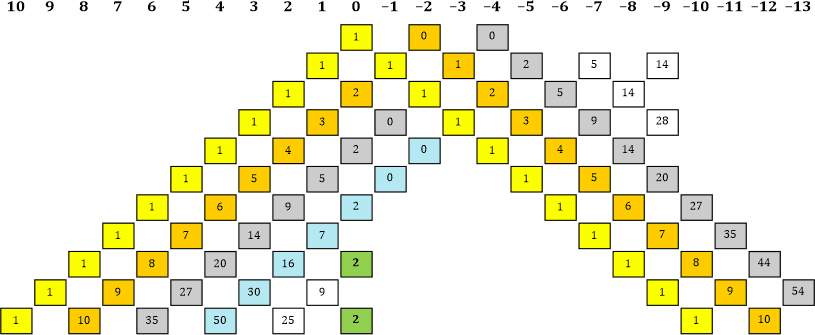
Tabelle 17a
|» Noch etwas kannst du gleich eintragen: in der obersten Zeile lauter Nullen.
«| Du meinst, das sei eine Art Grenzlinie wie die vertikale 2er-Spalte?
| |» Ich weiß nicht, ob das eine Grenzlinie ist, aber dort macht etwas Anderes als lauter Nullen keinen Sinn. Ich sehe auf der rechten Seite ein mögliches Bildungsgesetz, analog dem auf der linken Seite: Alle einzelnen Glieder sind jeweils die Summe von 2 vorhergehenden Gliedern. Die Richtung geht diesmal aber nicht wie auf der linken Seite von oben nach unten sondern von links nach rechts. Das ist wirklich fantastisch! |  |
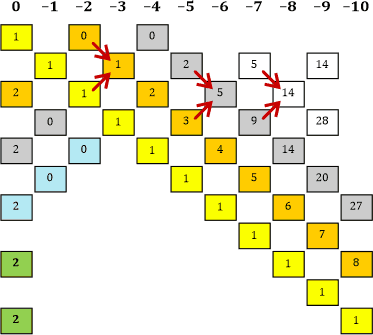 Tabelle 17b |
«| Und ob! Ich bin schon dabei, die Tabelle auszufüllen ...
|» Und ich bin bereits am Nachrechnen ...
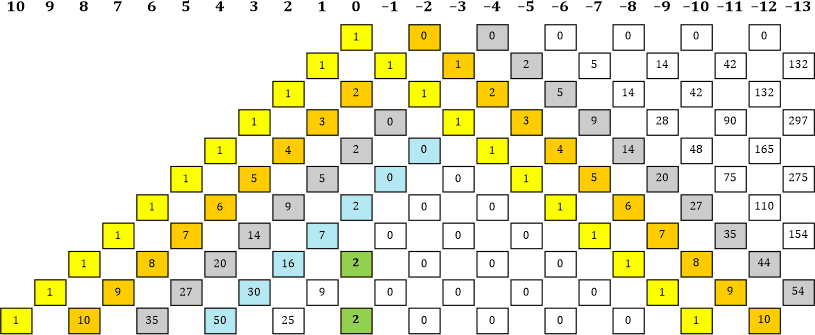
Tabelle 18
Schaut bisher alles prima aus!
«| Mir fällt auf, dass auf der rechten Seite die gelbe, orange und graue Linie identische Werte aufweisen (wenn auch »versetzt«), ab der blauen Linie gibt es aber keine Entsprechung auf der rechten Seite.
|» Das stimmt. Wir sollten die blaue Linie wieder entfernen. Und außerdem sollten wir die Tabelle deutlich erweitern. Dadurch verschaffen wir uns einen besseren Überblick.
Ich habe die Tabelle 19 ohne Spaltenüberschriften dargestellt.
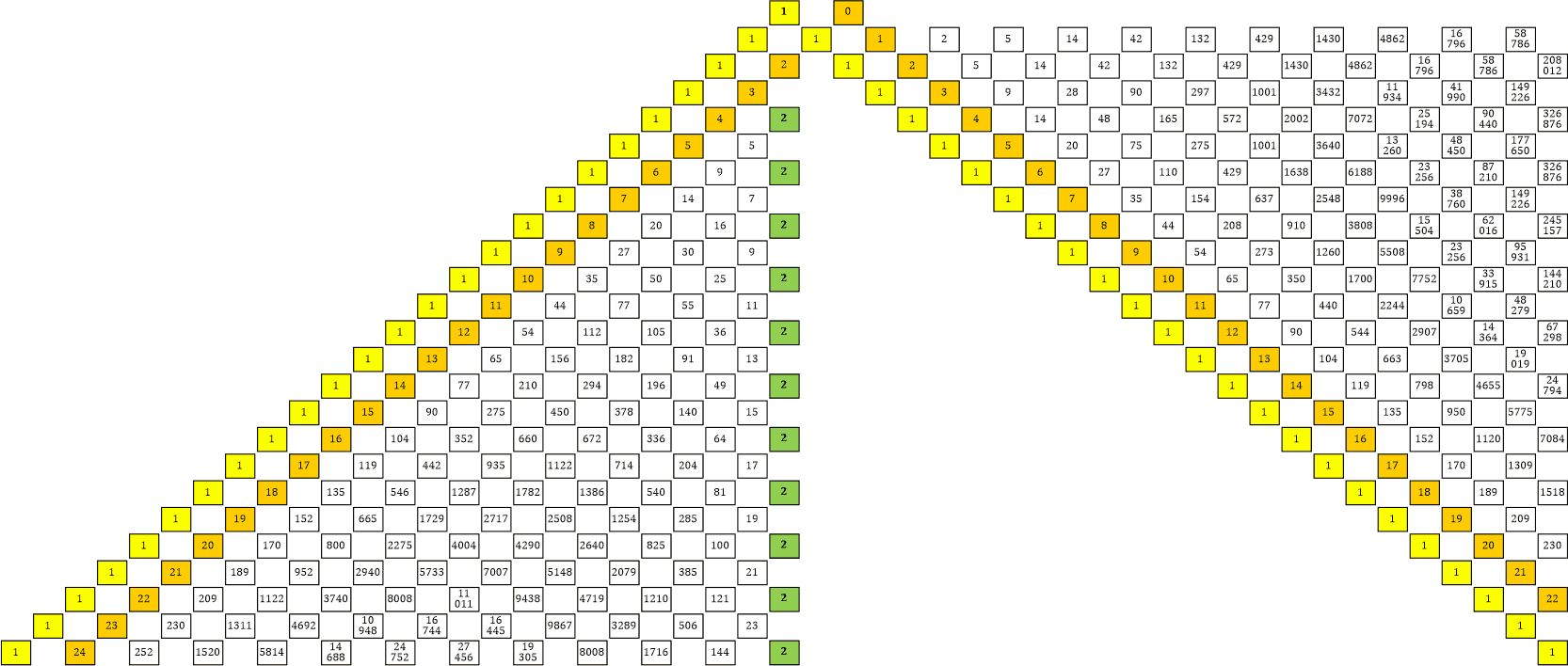
Tabelle 19
Vergrößern: Bild anklicken
Auf der linken Seite haben wir bereits gesehen, dass die Summe der Zahlen in einer Zeile jeweils dem Wert von Φn entspricht, wobei n die Zeilennummer ist.
«| Gibt es eine solche Entsprechung auch auf der rechten Seite der Tabelle?
|» Probieren wir’s aus. Wir sollten dazu aber die Zahlen nicht in den jeweiligen Zeilen addieren, sondern in den Spalten, da die »Wachstumsrichtung« auf der rechten Seite nicht nach unten, sondern nach rechts verläuft.
«| Ich bin schon gespannt!
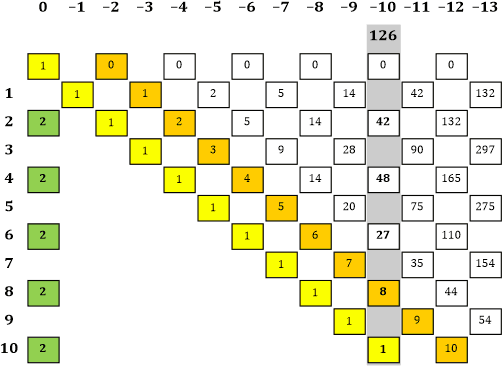 Tabelle 20 |
 |
|» Ich habe die Summe in der Spalte mit der Potenz −10 ausgerechnet: 1 + 8 + 27 + 48 + 42 + 0 = 126. Einen solchen Wert gibt es auf der linken Seite nicht. Allerdings haben wir auf der rechten Seite auch andere Faktoren als auf der linken. Rechne doch bitte in dieser kleinen Tabelle alle Spaltensummen aus, eventuell ist dadurch so etwas wie ein Trend erkennbar. «| Gerne. |
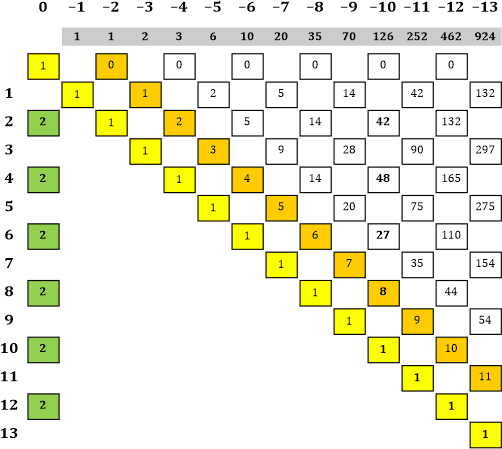 Tabelle 21 |
 |
|» Hmmm ... irgendwie kommen mir diese Zahlen bekannt vor, aber ich weiß nicht, woher. Hast du eventuell dazu eine Idee? «| Ja, und ob! Vor einiger Zeit habe ich in einem Buch etwas über das Pascal’sche Dreieck gelesen. Da sind in der mittleren Spalte die gleichen Zahlen vorgekommen. Schau bitte nach, ich bin ziemlich sicher ... |» Das könnte stimmen ... warte ... Treffer! |
Dieses Pascal’sche Dreieck (Tabelle 22) ähnelt stark unserer eigenen Tabelle:
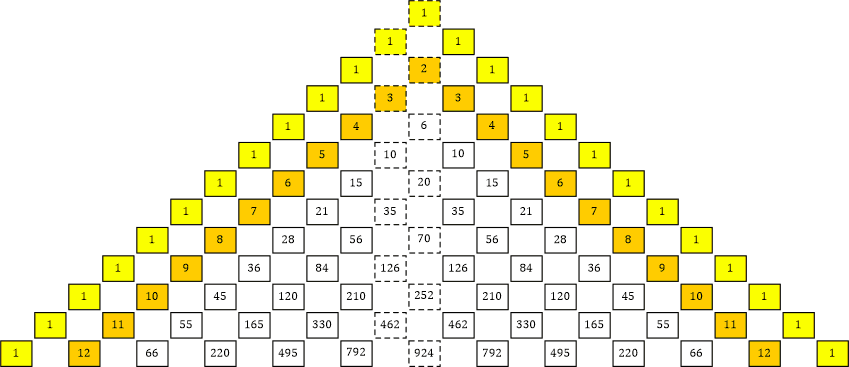
Tabelle 22
«| Wofür hat Pascal dieses Dreieck gebraucht?
|» Blaise Pascal konnte damit die sogenannten Binomial-Koeffizienten sehr einfach bestimmen. Diese werden unter anderem in der Kombinatorik gebraucht. Das Dreieck ist heute unter seinem Namen bekannt, er hat es jedoch nicht entdeckt oder erfunden. Die Binomial-Koeffizienten braucht man, um die Potenz eines Binoms wie (x + y)n zu berechnen. Wenn du z. B. n = 4 setzt, dann kannst du (x + y)4 auf folgende Weise berechnen:
(x + y)4 = x4 + 4 x3 y + 6 x2 y2 + 4 x y3 + y4
Die Binomial-Koeffizienten entsprechen in diesem Fall den Zahlen in der 4. Reihe des Pascal’schen Dreiecks.
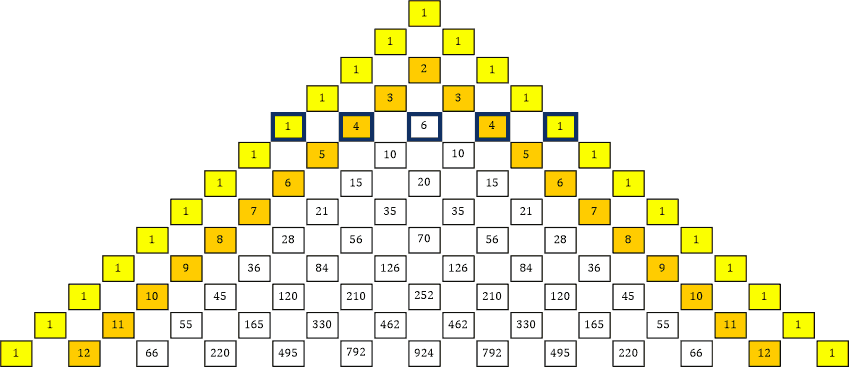
Tabelle 23
Für die 5. Pozent lautet die entsprechende Formel:
(x + y)5 = x5 + 5 x4 y + 10 x3 y2 + 10 x2 y3 + 5 x y4 + y5
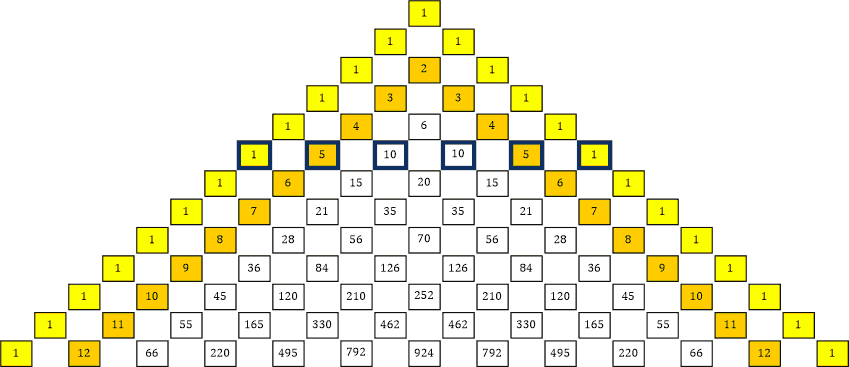
Tabelle 24
Für die 6. Pozent:
(x + y)6 = x6 + 6 x5 y + 15 x4 y2 + 20 x3 y3 + 15 x2 y4 + 6 x y5 + y6
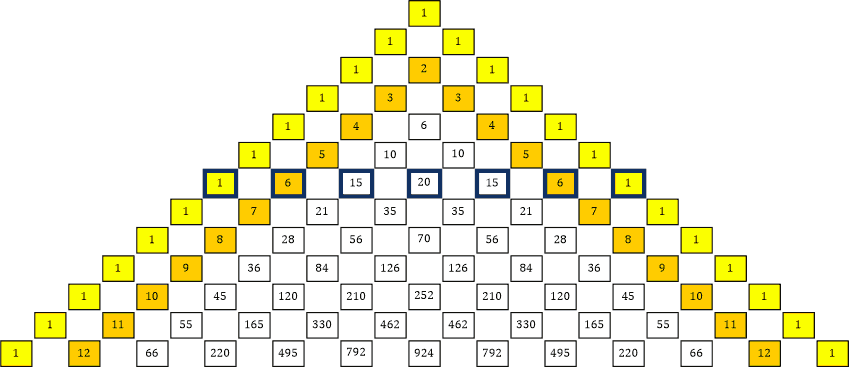
Tabelle 25
usw. ...
Eine der Eigenschaften des Pascal’schen Dreiecks ist, dass die Summe einer Zeile immer die n-te Potenz von 2 ist. Oder anders ausgedrückt: Die Zeilensumme verdoppelt sich mit jeder Zeile. Beispiel: Die Zeilensumme der Zeile 7 beträgt
1 + 7 + 21 + 35 + 35 + 21 + 7 + 1 = 128 = 27
und die Summe der Zeile 8 beträgt
1 + 8 + 28 + 56 + 70 + 56 + 28 + 8 + 1 = 256 = 28
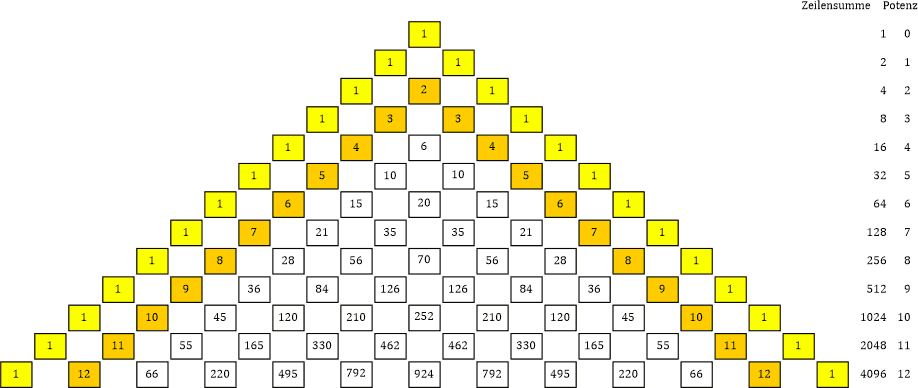
Tabelle 26
«| Ah, das ist im Grunde das Gleiche, das wir auch bei unserer Tabelle haben! Nur dass bei unserer Tabelle die Basis der Potenzen nicht 2 sondern Φ ist!
|» Genau! Die Zeilensumme der 7. Zeile im Pascal’schen Dreieck ist 27 = 128, die Zeilensumme bei unserem Phi-Dreieck (ich gebe ihm hiermit offiziell diesen Namen!) ist Φ7 = 29.
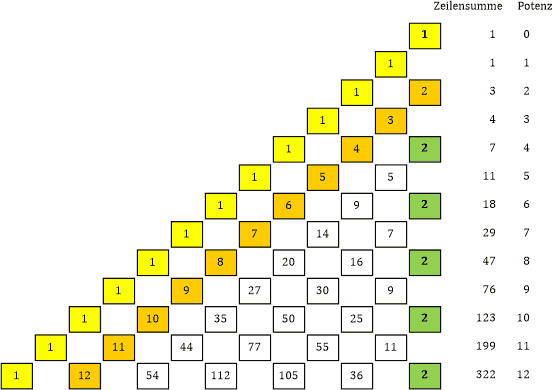 Tabelle 27a |
 |
Zu beachten ist der Wert an der Spitze des Dreiecks. Die gelbe Linie besteht durchgehend aus der Ziffer 1, während die grüne Linie durchgehend aus der Ziffer 2 besteht. Das ist jedoch kein Widerspruch, beide Werte sind richtig. |
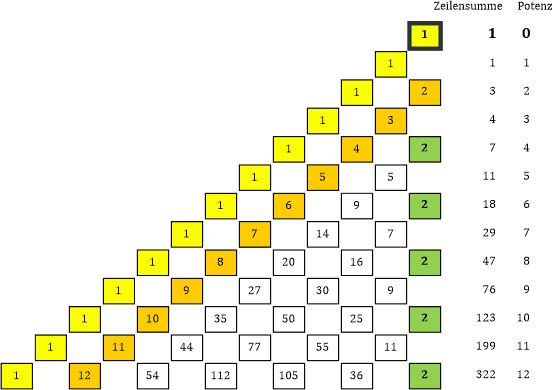 Tabelle 27b |
 |
In Tabelle 27b sehen wir die 1 an der Spitze. Sie ergibt sich, wenn wir die Folge der gerundeten Potenzen von Φ aufschreiben. |
|» Stimmt! Es fehlt der rechte Teil des Dreiecks. Wenn man die beiden Dreiecke (das Phi-Dreieck und das Pascal’sche) vergleicht, dann fällt sofort die »Optik« auf. Das Phi-Dreieck ist nur ein »halbes« Dreieck, es fehlt die rechte Hälfte.
«| Dann geben wir die rechte Hälfte doch dazu. Wir haben sie ja!
|» Ja, wir haben sie, aber sie passt nicht recht dazu ...
«| Dann machen wir sie eben passend!
|» Du meinst, wir drehen den rechten Teil um? ... Wir müssten dafür den rechten Teil (Tabelle 28a) »umklappen«. Er würde dann um seine gelbe »1er-Linie« gespiegelt werden und die strichlierte »Null-Linie« würde nicht mehr nach rechts sondern parallel zur orangen »2er-Linie« nach unten verlaufen (Tabelle 28b).
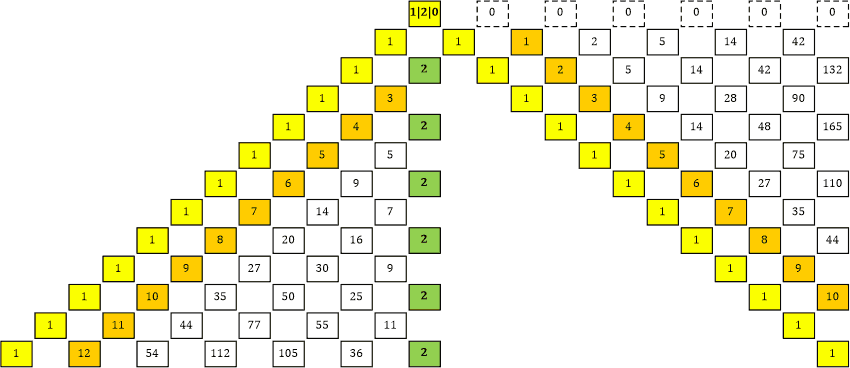
Tabelle 28a
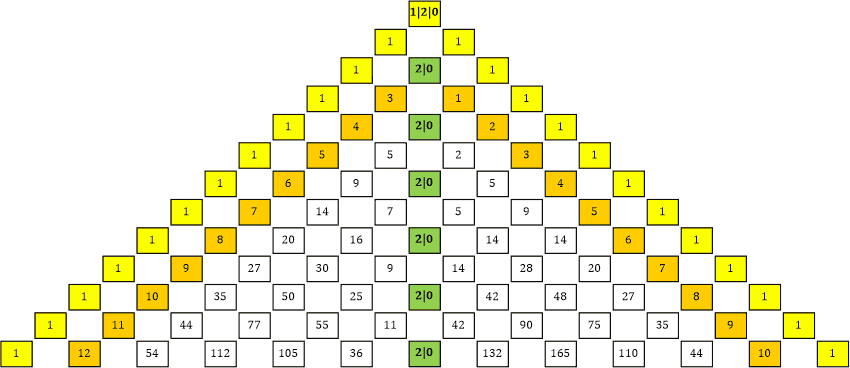
Tabelle 28b
Die beiden mittleren vertikalen Linien (2er- und Nullerlinie) kommen nicht nebeneinander zu liegen sondern übereinander. Die beiden Dreieckshälften sind etwas »ineinander verschoben«.
Die obere »Spitze« hat gleichzeitig drei Werte: 1, 2 und 0. Die vertikale Mittellinie hat in jeder zweiten Zeile immer gleichzeitig die Werte 2 und 0, je nachdem, welche der beiden Dreieckshälften man betrachtet. Die beiden Dreiecke sind entlang dieser »doppelten« vertikalen Linie »zusammengenäht«. Wenn ich zwei Stoff-Dreiecke an einer Seite zusammennähen will, dann muss ich die Seiten etwas übereinanderlegen, damit ich eine Naht anbringen kann ...
«| Du hast eine blühende Fantasie! Aber der Vergleich passt gut.
|» Die Zeilensummen, die dich auf die Idee gebracht hatten, unser Phi-Dreieck (Tabelle 29a) hätte eine Ähnlichkeit mit dem Pascal’schen Dreieck (Tabelle 29b), liegen jetzt »richtig«, nämlich horizontal:
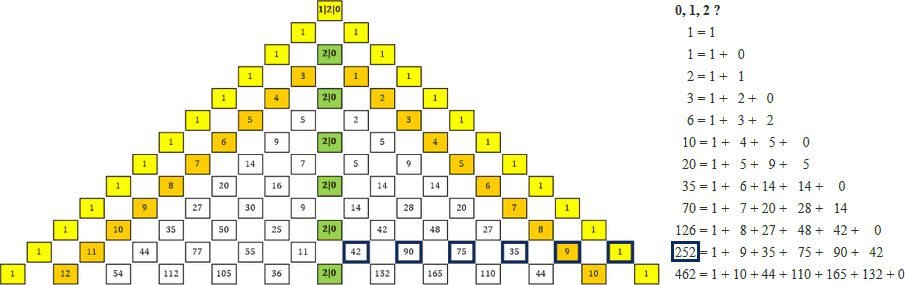
Tabelle 29a: Phi-Dreieck
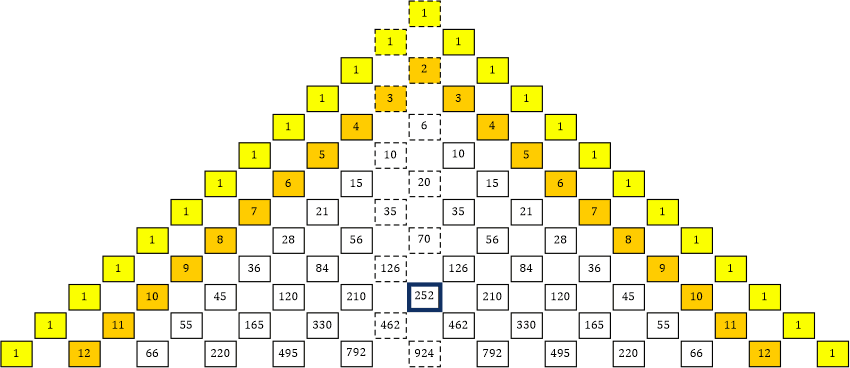
Tabelle 29b: Pascal’sches Dreieck
Im Grunde passt das Pascal’sche Dreieck wirklich gut zu unserem Phi-Dreieck. Beide Dreiecke werden von einer Rand-Reihe von gleichen Ziffern begrenzt. Das Pascal’sche Dreieck (das spiegelsymmetrisch ist) wird links und rechts jeweils mit einer Reihe von 1ern begrenzt. Das Phi-Dreieck besteht in Wahrheit aus zwei Dreiecken. Das eine Dreieck bildet die Faktoren für die positiven Potenzen von Φ, das andere Dreieck die Faktoren für die negativen Potenzen (Kehrwerte) von Φ. Die beiden Dreiecke stoßen an ihren Rändern aneinander bzw. überlappen sich dort mit jeweils einer ihrer äußersten Reihen (2er-Reihe bzw. 0er-Reihe).
Ich habe mich schon einige Male gefragt, was denn wohl »außerhalb« der Begrenzungsreihen liegt. Lauter Nuller? Möglicherweise. Eine befriedigende Antwort war das aber nicht.
Eine mögliche Antwort wäre ein weiteres Dreieck. Könnte das Pascal’sche Dreieck eventuell diese Aufgabe erfüllen?
«| Wir sollten das ausprobieren. Schlimmstenfalls funktioniert es nicht und wir vergessen diese Idee.
|» Das Pascalsche Dreieck wird auf beiden Seiten mit einer Reihe von 1ern begrenzt, das ist bei unserem kombinierten Dreieck ebenfalls der Fall. Wenn wir diese beiden Dreiecke sozusagen »Rücken an Rücken« aneinanderlegen, sodass jeweils die 1er-Reihen direkt aneinanderstoßen (bzw. sich überlappen), dann ergäbe das eine Art »geschlossenen Zahlenkreis«.
«| Ich denke, ich weiß, was du meinst. Ich zeichne das probehalber mal auf ... allerdings bekomme ich da ein Problem. Ich muss unsere Rechtecke mit den Zahlen nun jeweils in eine dreieckige Struktur pressen.
|» Versuch’s mal mit sechseckigen »Waben«.
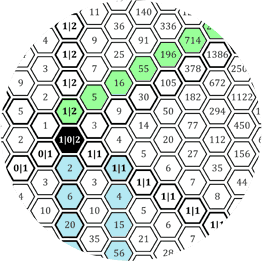
«| Gute Idee! Dadurch kann ich auch die leeren Zwischenräume zwischen den Rechtecken verschwinden lassen. Das Ergebnis sieht so aus (Tabelle 30):
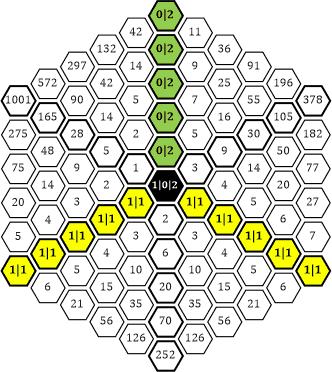
Tabelle 30
|» Das gefällt mir! Ich sehe, du hast das Pascal’sche Dreieck unten eingezeichnet und das Phi-Dreieck mit den positiven Potenzwerten rechts oben, das Dreieck mit den negativen Potenzwerten ist links oben.
«| Mir schien diese Anordnung sinnvoll. Das Pascal’sche Dreieck ist spiegelsymmetrisch, daher habe ich es an den unteren Rand gegeben. Und die positiven Potenzen sollte man besser rechts anordnen, da sie »aufsteigend« sind, die negativen sind nach links hin »fallend« – ähnlich wie in einem kartesischen Koordinatensystem, bzw. auf der »Zahlengeraden«.
|» Hast du die Richtigkeit der Anordnung der Zahlen überprüft? Mir erscheint diese etwas komisch.
«| Ich zeichne ein paar Pfeile ein, aus deren Richtung man erkennen kann, wie die Summen der einzelnen Zahlen zustande kommen (Tabelle 31):
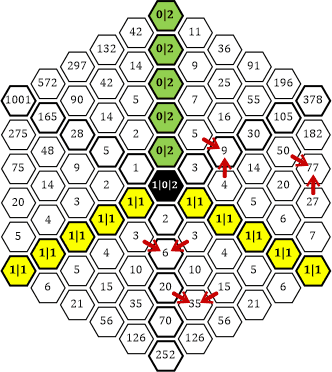
Tabelle 31
|» Bis hierher schaut alles prima aus. Ich fürchte jedoch, im linken oberen Drittel wirst du jetzt Schwierigkeiten bekommen.
«| Weshalb?
|» Weil 2 + 2 nicht 5 ergibt, und 3 + 5 ergibt nicht 9 ...
«| Wenn du genau hinsiehst, kannst du erkennen, dass wir beim Phi-Dreieck in den beiden Hälften die Summen auf unterschiedliche Weise erhalten haben. Auf der linken Seite haben wir die Summe jeweils aus der Zahl zwei Zeilen direkt darüber und der Zahl rechts oberhalb davon erhalten. Auf der rechten Seite hingegen haben wir jeweils die Zahlen links und rechts in der Zeile darüber zusammengezählt. In der Tabelle 32 habe ich die beiden Summier-Arten im Phi-Dreieck eingezeichnet.
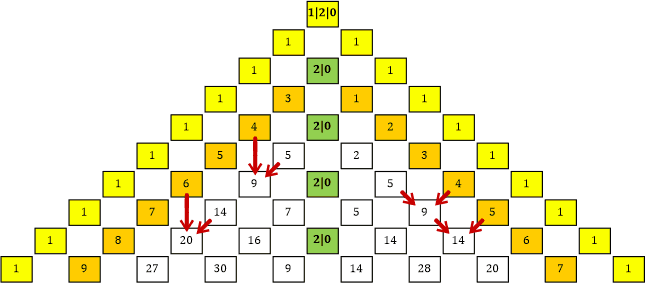
Tabelle 32
Dadurch ergibt sich in unserem »Dreiecks-Kreis« im linken oberen Drittel die Summenbildung auf folgende Weise:
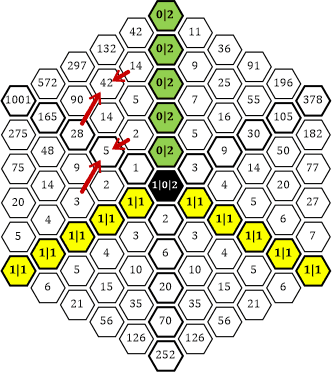
Tabelle 33
|» Im ersten Augenblick erscheint es etwas befremdlich, dass die Summenbildung so »schräg« erfolgt, aber deine Argumentation ist nachvollziehbar und natürlich richtig.
Da du diesen »Dreiecks-Kreis«, wie du ihn genannt hast, so schön gezeichnet hast – würdest du den Kreis ein wenig erweitern, damit wir etwas mehr »Spielraum« haben, um eventuelle Gesetzmäßigkeiten herauszufinden?
«| Gerne. Ich habe hiermit sogar die »Quadratur des Kreises« geschafft! :-)
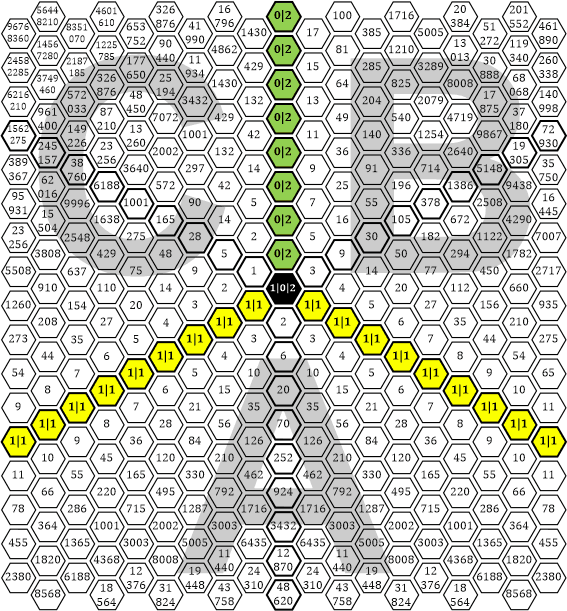
Tabelle 34
Und damit wir uns ab sofort mit der Beschreibung etwas leichter tun, habe ich den drei Sektoren im »quadratischen Kreis« die Buchstaben A, B, C zugeordnet. Wir können uns jetzt also auf den Weg machen und mögliche »Querverbindungen« zwischen den Sektoren aufspüren.
Eine erste Verbindung habe ich während des Zeichnens bereits herausgefunden. Sie wird dir bestimmt gefallen, denn sie betrifft gleich alle drei Sektoren!
|» Du machst mich neugierig!
«| Es gibt einen Zusammenhang zwischen dem Pascal’schen Dreieck (ab jetzt Sektor A genannt) und den Sektoren B und C:
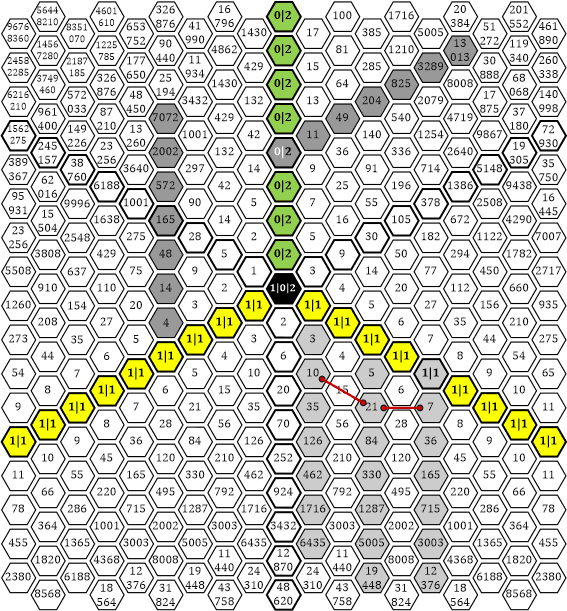
Tabelle 35
Im Sektor A habe ich drei vertikale Linien eingezeichnet. Diese haben einen Zusammenhang mit den etwas dunkler gezeichneten Linien in den anderen beiden Sektoren. Wenn du im Sektor A jeweils die Differenz zwischen einer Zahl in der mittleren Linie und der links »schräg darüber« benachbarten Zahl bildest, dann wird das Ergebnis jeweils in der im Sektor B eingezeichneten Linie sichtbar.
Gleiches können wir im Sektor A mit der mittleren und der rechts davon befindlichen Linie machen. Hier bilden wir die Differenz zwischen den auf gleicher Höhe stehenden Zahlen. Das Ergebnis ist in der Linie im Sektor C zu bewundern. Hier die zwei Listen mit den Differenzen:
| Sektor A–B | Sektor A–C | |||||||||
| 5 | − | 3 | = | 2 | 5 | − | 1 | = | 4 | |
| 21 | − | 10 | = | 11 | 21 | − | 7 | = | 14 | |
| 84 | − | 35 | = | 49 | 84 | − | 36 | = | 48 | |
| 330 | − | 126 | = | 204 | 330 | − | 165 | = | 156 | |
| 1.287 | − | 462 | = | 825 | 1.287 | − | 715 | = | 572 | |
| 5.005 | − | 1.716 | = | 3.289 | 5.005 | − | 3.003 | = | 2.002 | |
| 19.448 | − | 6.435 | = | 13.013 | 19.448 | − | 12.376 | = | 7.072 | |
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | |||||
|» Schön! Wir können das Ergebnis aber noch schöner machen!
«| Wie denn?
|» Indem wir die Zahlen im Sektor C um die dortige »Mittelachse« (mit den dicker eingerahmten Sechsecken) spiegeln! Dann bilden die beiden Linien mit den Differenzen nämlich eine einzige fortlaufende Linie zwischen den Sektoren B und C. Mir würde das gut gefallen.
«| Mir auch! Ich hebe mir die Tabelle 35 aber für alle Fälle noch auf, bis wir endgültig wissen, wie sie »richtig« angeordnet werden muss. Das Hin- und Herschaufeln sämtlicher Zahlen ist nämlich eine Menge Arbeit ...
|» Lass dir Zeit, es eilt ja nicht. Vielleicht findest du dabei noch weitere Zusammenhänge heraus.
~~~ ~~~ Zwei Tage später ~~~ ~~~
«| Ich habe den Sektor C wie besprochen gespiegelt und den »quadratischen Dreieckskreis« ein wenig erweitert. Zusätzlich habe ich noch ein paar Pfeile eingezeichnet, aus deren Richtung man in jedem Sektor die Entstehung der Zahlen erkennen kann:
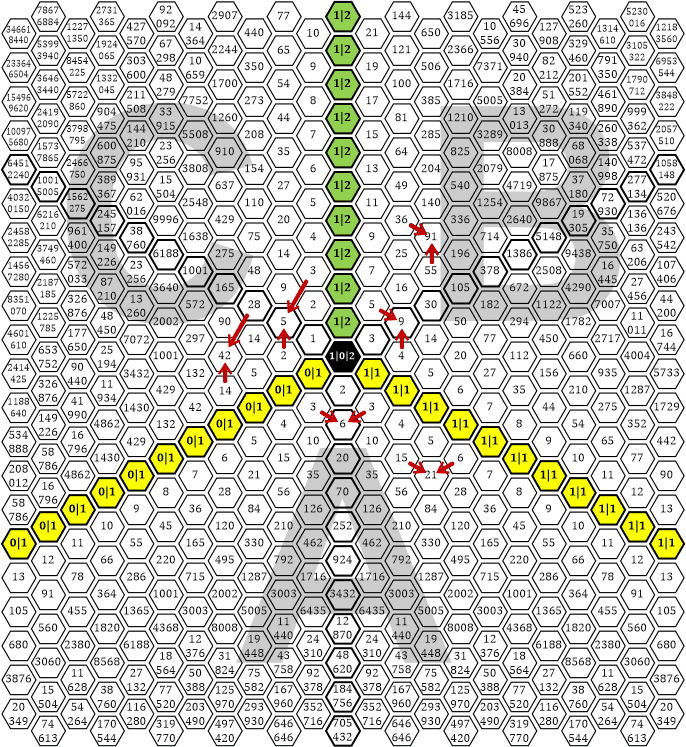
Tabelle 36
Im Folgenden werde ich die bereits gefundenen Differenz-Linien anschaulich darstellen: Einfach auf die Pfeil-Buttons klicken und zusehen, »wie die Linien wandern«. Die Differenz der Zahlen wird jeweils daneben aufgelistet.
Ich beginne mit den Differenzlinien in den Sektoren A–C (Tabelle 37). Man erkennt gut, dass im Sektor C die Linie von oben nach unten und anschließend wieder zurück wandert, während gleichzeitig die Linien im Sektor A von links nach rechts durchwandern – die Symmetrie im Sektor A macht das möglich.
  |
A  |
Tabelle 37
Kommen wir nun zur »Verlängerung« der Linien vom Sektor C direkt hinüber in den Sektor B:
  |
A 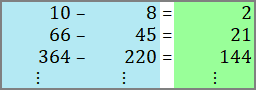 |
Tabelle 38
Wir sehen, dass im Sektor A die Linien wie vorhin von links nach rechts wandern, allerdings um eine »Wabenhöhe« zueinander versetzt. In Tabelle 39 kann man den Unterschied gut erkennen:
  |
A 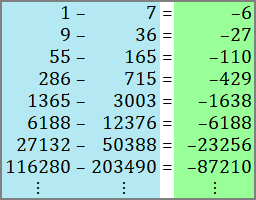 Vergleiche Tabelle 37
|
Tabelle 39
|
Ausschnitt aus |
Verfolgt man in Tabelle 38 den »Fortschritt« der Linie in Sektor B, scheint es, dass ab Station »I« die beiden Linien im Sektor A nur mehr am unteren Ende einen Versatz aufweisen. Wo ist dieser am oberen Ende geblieben? Das Rätsel kann leicht gelöst werden, indem wir die zugehörige Differenzenliste betrachten:
Die 0 in der ersten Zeile (2 − 0 = 2) ist unsichtbar! |
Die »wandernde Linie« im Sektor B wird nicht an einer Grenzlinie »reflektiert« (wie das im Sektor C der Fall ist), sondern läuft ungehindert nach rechts unten weiter – es gibt hier (genauso wie im Sektor A) keine »Randlinie«, an welcher eine Reflexion auftreten könnte.
|» Was mich brennend interessieren würde: Wir haben nun in allen Sektoren »Differenzlinien« gefunden. Die Zahlen in den Sektoren werden aber durch eine Summenbildung erzeugt ...
«| Du meinst, ob es auch in gleicher Weise »Summenlinien« zu finden gibt? Die Antwort ist: Ja! Zwischen den Sektoren A und B gibt es einen sehr schönen Summen-Zusammenhang:
  |
A 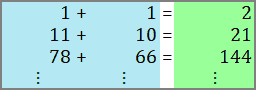 |
Tabelle 43
Die beiden Linien, welche die zu addierenden Zahlen liefern, liegen im Sektor A vertikal nebeneinander – der Unterschied zu den Differenzlinien besteht darin, dass zwischen den beiden Linien kein Abstand ist.
Die »Laufrichtung« der Linien ist identisch mit jener in der Tabelle 38. Zwischen den Sektoren A und C habe ich bisher keinen Summen-Zusammenhang gefunden.
|» Was jetzt noch fein wäre: ein Summen-Zusammenhang zwischen den Sektoren B und C. Hat deine Spürnase diesbezüglich etwas finden können?
«| Sie hat! Allerdings in etwas anderer Form, als ich mir das ursprünglich vorgestellt hatte. Ich habe zwischen den beiden Sektoren nämlich einen Zusammenhang zwischen Differenz- und Summenlinien gefunden! Die Tabelle 44 zeigt dir, wie das zustande kommt:
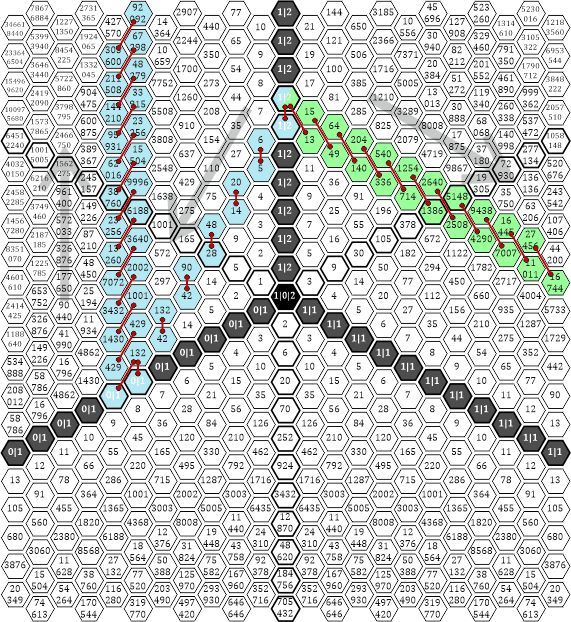 Tabelle 44 |
Es gibt in beiden Sektoren jeweils Linien, die aus »Zahlen-Pärchen« bestehen. Die Differenz zwischen den Zahlen-Pärchen in Sektor B entspricht jeweils der Summe eines Zahlenpärchens in Sektor C. In der Tabelle 44 habe ich die Pärchen »zusammengenäht«, damit man sieht, welche Zahlen Paare bilden. Das wirklich Spannende dabei ist, dass es aussieht, als handle es sich um einen einzigen »Strahl«, der zweimal »umgelenkt« bzw. »gespiegelt« wird. Wenn man genauer hinsieht, bemerkt man aber, dass es sich um zwei Linien handelt, die den gleichen Ursprung genau an der Grenzlinie zwischen B und C haben. |
Um das Ganze anschaulicher zu machen, habe ich eine Liste mit den »Differenz-Summen« erstellt:
 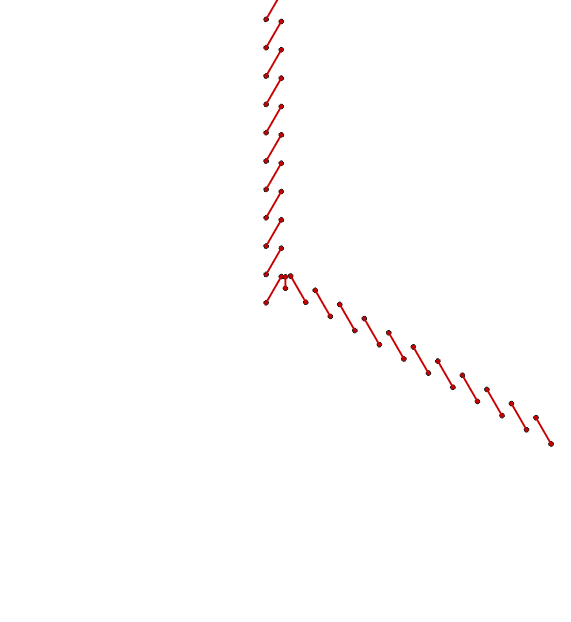  |
A 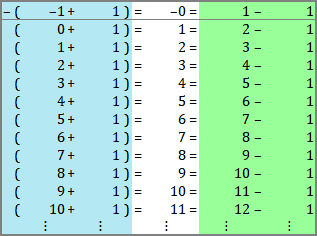 |
Tabelle 45
Im Sektor C verläuft die Linie mit den Summen-Pärchen erst mal horizontal bis zur gegenüberliegenden Randlinie »0«. Dort wird sie gespiegelt und verläuft ab hier parallel zur Randlinie »1« weiter ins Unendliche. Ich habe den ersten Teil der Strecke ganz bewusst als horizontal bezeichnet, denn die drei Sektoren kennen in Wahrheit kein »oben« oder »unten«. Wir betrachten im Sektor A die Linie 1–7–21–35–35–21–7–1 als horizontal – und wenn wir den gesamten »Dreieckskreis« um 120° gegen den Uhrzeigersinn drehen, dann liegt anschließend die Linie 1–6–20–48–90–132–132–0 ebenfalls horizontal an der gleichen Stelle.
Die Spiegelung an der »0«-Linie des Sektors C erfolgt bei jenem Zahlenpärchen (0 + 132), das in der Differenz-Summen-Liste am Übergang zwischen grauem und weißem Hintergrund steht. Im Sektor B überspringt das Pärchen, das als erstes die »weiße Zone« betritt (2640 − 2508), an dieser Stelle die Mittellinie im Sektor (Linie der Waben mit dickem Rand). Genau dort wechselt auch das Vorzeichen der Summe/Differenz.
|» Im Sektor C gibt es immer noch ein »Problem«, das mir nicht aus dem Kopf gehen will ... Wir haben dort nämlich ein Loch in der Zahlenfläche.
«| Ein Loch??
|» Ja. Wir haben dort eine Zahl hingeschrieben, die in Wahrheit gar nicht da ist. Wenn wir die Entstehung des »Zahlenteppichs« betrachten, dann sehen wir, dass wir jeweils zwei nebeneinander liegende Zahlen addiert und anschließend die Summe eine Zeile darunter hingeschrieben haben – und zwar in die Mitte zwischen den beiden Zahlen, deren Summe wir gebildet haben. Im Sektor A (dem Pascal’schen Dreieck) sind die Zahlen symmetrisch um die Mittelachse angeordnet. Daher ergibt sich ein schön regelmäßig »nach unten fließendes« Muster. Hier zur Erinnerung nochmal die Pfeile, die wir bereits in die Tabelle 36 eingezeichnet hatten:
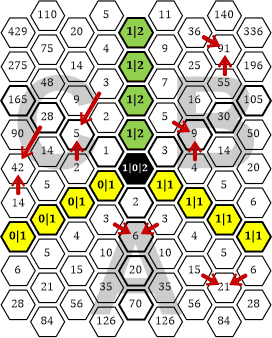
Tabelle 46
Das gleiche Muster sehen wir im Sektor B. Wenn wir die wabenförmige Tabelle um 120° im Uhrzeigersinn drehen, dann kommen die Zahlen 4 und 5 (mit der Summe 9) im Sektor C an der gleichen Stelle zu liegen wie vorher die Zahlen 3 und 3 (mit der Summe 6) im Sektor A:
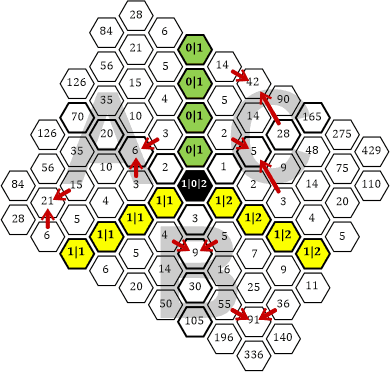
Tabelle 47
Im Sektor C haben wir jedoch eine »verschobene« Summenbildung. Ich drehe die Waben um weitere 120°, dann sieht man es besser:
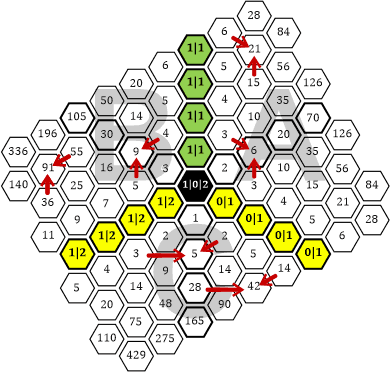
Tabelle 48
Der Sektor C ist begrenzt von Randlinien, die auf der einen Seite aus einer Reihe mit der Zahl 2 und auf der anderen Seite aus einer Reihe mit der Zahl 0 bestehen. Würden wir die Zahlen im Sektor C auf gleiche Weise wie in den Sektoren A und B addieren, so ergäbe sich folgendes Muster:
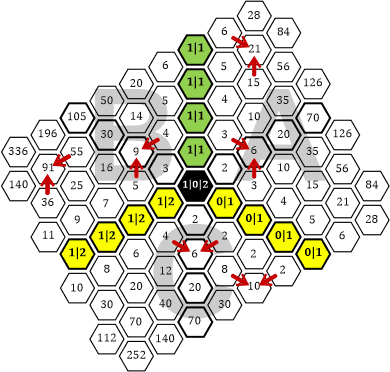
Tabelle 49
Bei genauem Hinschauen stellt sich heraus, dass das auf diese Weise entstehende Zahlendreieck ein symmetrisches wäre, ähnlich dem Pascal’schen Dreieck im Sektor A. Das Dreieck wäre links und rechts begrenzt mit einer Reihe von 2ern. Zur besseren Veranschaulichung ändere ich die Einfärbung:
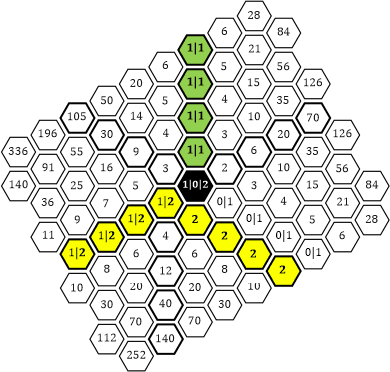
Tabelle 50
Der Sektor C besteht aus den Zahlen, welche die Faktoren für die Potenzreihe des Nachkomma-Teils von Φ bilden. Und die Entstehung dieser Zahlenreihe hat einen nicht-symmetrischen Ursprung. Streng genommen kennen wir diesen Ursprung gar nicht, denn er liegt irgendwo im unendlich Kleinen.
Erinnern wir uns an die Quadrate, die wir gezeichnet haben, um die Verhältniszahl Φ auf geometrische Weise darzustellen. Diese haben so ausgesehen:
 Bild 11
Bild 11
In der Richtung nach rechts unten werden die Quadrate immer kleiner (im Verhältnis 1 : Φ), es bleibt aber immer ein restliches »Loch«, in welches man weitere, noch kleinere Quadrate einzeichnen könnte.
Umgekehrt betrachtet: Die Quadrate werden, von diesem winzigen »Loch« ausgehend, in Richtung nach links oben um den Faktor Φ immer größer. Die immer größer werdenden Quadrate entstehen auf die gleiche Weise wie die Zahlen in unseren Dreieckstabellen. Und die beiden Tabellen, welche die Faktoren für die vollständige Zahl Φ liefern, haben genauso ein »Loch« an ihrem Ursprung! Zeichnen wir die Tabellen nochmal in ihrer ursprünglichen Form auf:
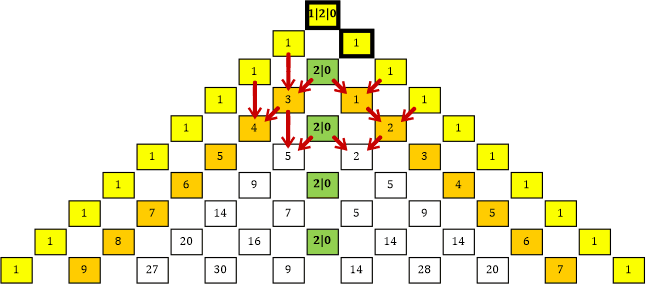
Tabelle 51
Die beiden dick eingerahmten Zahlen bilden das »Loch«! Im wabenförmigen »Zahlenkreis« ist das Loch im Zentrum und an der ersten Stelle der Grenzlinie zwischen den Sektoren B und C zu finden:
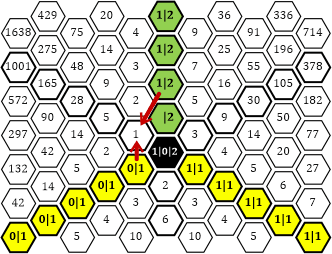
Tabelle 52
Ich habe die Zahl 1 im »Loch« daher weggelassen, da sie für die Summenbildung der Zahlen im Sektor C keine Verwendung findet. Genaugenommen finden auch die Zahlen im »schwarzen Loch« im Zentrum keine Verwendung. Dennoch bilden sie den Ursprung. Mich erinnert das an das »Schwarze Loch« im Zentrum unserer Galaxie, der Milchstraße ...