Werden
Nimm etwas und gib etwas Anderes dazu. Das Ergebnis ist etwas Neues.
Das machst du mit dem Anderen und dem Neuen wieder. Beliebig oft.
|» Das ist das ganze Gesetz des Entstehens, des Werdens.
Ich werde dir das anhand von Zahlen zeigen.
Nimm eine x-beliebige Zahl und gib eine andere beliebige Zahl dazu, das heißt, zähle sie zusammen.
«| Gut, ich nehme 37,42 und gebe 12 dazu. Das Ergebnis ist 49,42.
|» Dann mache das wie oben beschrieben wieder: Gib zur letzten Zahl das Ergebnis dazu:
12 + 49,42 = 61,42
«| Wie oft soll ich das machen? Ich mach’s einfach ein paarmal ... also:
| 49,42 | + | 61,42 | = | 110,84 |
| 61,42 | + | 110,84 | = | 172,26 |
| 110,84 | + | 172,26 | = | 283,10 |
| 172,26 | + | 283,10 | = | 455,36 |
| 283,10 | + | 455,36 | = | 738,46 |
| 455,36 | + | 738,46 | = | 1193,82 |
| 738,46 | + | 1193,82 | = | 1932,28 |
| 1193,82 | + | 1932,28 | = | 3126,10 |
| 1932,28 | + | 3126,10 | = | 5058,38 |
| 3126,10 | + | 5058,38 | = | 8184,48 |
«| So, ich hab das jetzt 10-mal gemacht, das muss reichen. Und wozu soll das gut gewesen sein?
|» Ich möchte, dass du dir anschaust, um welchen Faktor das Ergebnis jeweils wächst.
«| Um welchen Faktor das Ergebnis wächst? Wie meinst du das?
|» Der Faktor ist der Betrag, mit dem du das vorletzte Ergebnis multiplizieren musst, um das letzte Ergebnis zu erhalten. Wenn du also das letzte Ergebnis durch das vorhergehende dividierst, dann erhältst du den Faktor, um welchen das Ergebnis zuletzt angewachsen ist. Kompliziert? Probier’s einfach aus.
«| O. k., wenn du meinst ...
|
= 1,5541 |
|
= 1,6434 |
|
= 1,6085 | |||||||||||
|
= 1,6217 |
|
= 1,6166 |
|
= 1,6186 | |||||||||||
|
= 1,6178 |
|
= 1,6181 |
|
= 1,6180 | |||||||||||
|» Fällt dir was auf?
«| Ja, der Faktor scheint sich bei etwa 1,618 einzupendeln.
|» Genau. Wenn du noch weiterrechnest, dann wirst du merken, dass sich der Faktor immer genauer bei 1,61803398875... einpendelt. Diese Zahl nennen die Mathematiker Φ (Phi – sprich: Fi – der 21. Buchstabe im griechischen Alphabet). Sie ist eine der beiden Lösungen der Gleichung x² − x − 1 = 0 und hat den Betrag
|
= | 1,61803398875... |
«| Ich versteh das zwar nicht, aber ...
|» Das macht einstweilen nichts. Machen wir einen zweiten Versuch. Such dir bitte zwei andere Zahlen aus, irgendwelche »schrägen« Zahlen ...
«| Noch zwei?
|» Ja, wir wollen diese Rechenregel auch noch mit zwei ganz anderen Zahlen ausprobieren und uns das Ergebnis anschauen.
«| Ich nehme die Zahlen 1,37 und minus 329. Ich darf doch auch eine negative Zahl verwenden?
|» Natürlich, ich sagte ganz bewusst, irgendwelche Zahlen.
«| Da bin ich aber gespannt ...
| (1,37) | + | (−329,00) | = | −327,63 |
| (−329,00) | + | (−327,63) | = | −656,63 |
| (−327,63) | + | (−656,63) | = | −984,26 |
| (−656,63) | + | (−984,26) | = | −1640,89 |
| (−984,26) | + | (−1640,89) | = | −2625,15 |
| (−1640,89) | + | (−2625,15) | = | −4266,04 |
| (−2625,15) | + | (−4266,04) | = | −6891,19 |
| (−4266,04) | + | (−6891,19) | = | −11157,23 |
| (−6891,19) | + | (−11157,23) | = | −18048,42 |
| (−11157,23) | + | (−18048,42) | = | −29205,65 |
| (−18048,42) | + | (−29205,65) | = | −47254,07 |
Genügt das? Es kommt jetzt etwas ganz Anderes heraus. Das sind lauter negative Zahlen!
|» Macht nichts, rechne bitte trotzdem die jeweiligen Faktoren bei den Ergebnissen aus.
«| O. k.
|
= 2,0042 |
|
= 1,4990 |
|
= 1,6671 | |||||||||||
|
= 1,5998 |
|
= 1,6251 |
|
= 1,6154 | |||||||||||
|
= 1,6191 |
|
= 1,6176 |
|
= 1,6182 | |||||||||||
|
= 1,6180 | |||||||||||||||
Aha! Das scheint tatsächlich wieder auf das gleiche Ergebnis hinauszulaufen ... ist das bei allen Zahlen so?
|» Ja, das ist bei allen Zahlen so. Es ist wirklich vollkommen egal, welche Zahlen du verwendest, das Ergebnis nähert sich immer der Zahl Φ = 1,61803398875... Es funktioniert sogar dann, wenn eine der beiden Zahlen null ist.
«| Bei null? Das glaub ich nicht.
|» Probier’s aus!
«| O. k., ich nehme 7 und 0.
| 7 | + | 0 | = | 7 |
| 0 | + | 7 | = | 7 |
| 7 | + | 7 | = | 14 |
| 7 | + | 14 | = | 21 |
| ⋮ |
Ja, ja ich hab’s kapiert, ich glaub’s dir!
|» Prima. Du siehst also, dass diese »Wachstumsregel« immer zum gleichen Ergebnis führt, egal von welcher Position du angefangen hast. Jetzt werde ich dir ein paar Eigenschaften dieser sonderbaren Zahl Φ zeigen.
Der Kehrwehrt von Φ ist um genau 1 kleiner als Φ:
|
= | 0,618034 |
Und wenn du das Quadrat von Φ ausrechnest, dann wirst du feststellen, dass dieses um genau 1 größer ist als Φ:
1,6180342 = 2,618034
Das ist schon mal ziemlich bemerkenswert. – So, jetzt werden wir uns diese Zahl noch etwas genauer anschauen. Kann man sie eigentlich exakt berechnen? Die Antwort ist Nein, denn sie gehört zur Gruppe der sogenannten irrationalen Zahlen – so bezeichnen Mathematiker Zahlen, die durch keine Bruchzahl berechnet werden kann. Die Zahlen rechts vom Komma werden nie periodisch, d. h. du kannst nie vorhersagen, welches die nächste Zahl sein wird: 1,61803398874989484820458683436563811772030917980576286213544862270526046....
Probieren wir die »Wachstumsregel« doch einmal mit den Zahlen 1 und Φ aus:
| 1,00000000000000000000... |
| 1,61803398874989484820... |
| 2,61803398874989484820... |
| 4,23606797749978969640... |
| 6,85410196624968454461... |
| 11,09016994374947424102... |
| 17,94427190999915878563... |
| 29,03444185374863302665... |
| 46,97871376374779181229... |
| 76,01315561749642483895... |
| 122,99186938124421665125... |
| 199,00502499874064149020... |
| 321,99689437998485814146... |
| 521,00191937872549963166... |
| 842,99881375871035777312... |
| 1364,00073313743585740479... |
| 2206,99954689614621517792... |
| 3571,00028003358207258272... |
| 5777,99982692972828776065... |
| 9349,00010696331036034337... |
| 15126,99993389303864810402... |
| 24476,00004085634900844740... |
| 39602,99997474938765655143... |
| 64079,00001560573666499884... |
| 103681,99999035512432155028... |
| 167761,00000596086098654912... |
| 271442,99999631598530809940... |
| 439204,00000227684629464853... |
| 710646,99999859283160274794... |
| 1149851,00000086967789739648... |
| 1860497,99999946250950014442... |
| 3010349,00000033218739754091... |
| 4870846,99999979469689768534... |
| 7881196,00000012688429522625... |
| 12752042,99999992158119291159... |
| 20633239,00000004846548813785... |
Fällt dir etwas auf?
«| Ja, es entstehen rechts vom Komma immer mehr Nullen oder Neuner ... das scheint sich alles in Richtung ganzer Zahlen zu bewegen.
|» Genau, die Differenz zu einer ganzen Zahl wird immer kleiner. – So, und jetzt teilen wir diese Zahlen, die wir hier erhalten haben, in den Teil links vom Komma und den Teil rechts vom Komma auf und schauen uns das etwas näher an. Beginnen wir mit der 13. Zahl in der Reihe: 521,00191937872549963166.
Links vom Komma steht 521, rechts davon 0,00191937872549963166. Auf den ersten Blick scheint das nichts Besonderes zu sein. Dieser Eindruck ändert sich jedoch schlagartig, wenn wir den Kehrwert des Nachkommateils bilden:
|
= | 521,00191937872549963166 |
Was sagst du dazu?
«| Das ist wieder dieselbe Zahl wie vorher! Ist das Zufall?
|» Wäre es Zufall, dann wäre dieser sehr zufällig ... Probieren wir es auch noch mit einer anderen Zahl – z. B. mit der 18. Zahl: 5777,99982692972828776065
«| Mit dieser Zahl wird es nicht funktionieren, denn deren Nachkommateil ist nahe bei 1 ...!
|» Da hast du schon recht, aber schau dir bitte nochmal die Reihe mit den immer mehr werdenden Nullen und Neunern von vorhin an:
| 1,00000000000000000000 |
| 1,61803398874989484820 |
| 2,61803398874989484820 |
| 4,23606797749978969640 |
| 6,85410196624968454461 |
| 11,09016994374947424102 |
| 17,94427190999915878563 |
| 29,03444185374863302665 |
| 46,97871376374779181229 |
| 76,01315561749642483895 |
| 122,99186938124421665125 |
| 199,00502499874064149020 |
| 321,99689437998485814146 |
| 521,00191937872549963166 |
| 842,99881375871035777312 |
| 1364,00073313743585740479 |
| 2206,99954689614621517792 |
| 3571,00028003358207258272 |
| 5777,99982692972828776065 |
| 9349,00010696331036034337 |
| 15126,99993389303864810402 |
Wie du siehst, pendeln die Werte immer genauer um eine ganze Zahl. Immer schön abwechselnd einmal knapp darüber, dann knapp darunter. Wir müssen uns also mit der Differenz zur jeweiligen ganzen Zahl beschäftigen. Liegt der Wert knapp darüber, wie vorher bei 521,00191937872549963166, dann entspricht die Differenz genau dem Nachkommateil. Liegt er knapp darunter, wie bei 5777,99982692972828776065, dann ist die ganze Zahl 5778 und die Differenz des Nachkommateils zu dieser ganzen Zahl beträgt
5778 – 5777,99982692972828776065 = 0,00017307027171223935
Wir betrachten also den Kehrwert dieser Differenz:
|
= | 5777,99982692972828776065 |
Zufrieden?
«| Und wie!
|» Ja, das ist wirklich schön. Auch hier ist der Kehrwert des Nachkommateils wieder genau die ursprüngliche Zahl. – Jetzt zeige ich dir zwischendurch noch etwas, zu dem ein Mathematiker »Na logisch!« sagen würde. In unserer Reihe, die wir mit der Summe aus 1 und Φ begonnen haben, können wir die Ergebnisse auch dann erhalten, wenn wir stattdessen das jeweilige Ergebnis immer mit Φ multiplizieren. Wir haben ja ganz am Anfang (als wir die »Wachstumsregel« noch mit beliebigen Zahlen angewendet hatten) gesehen, dass wir bei immer öfterer Anwendung der Regel den immer genauer werdenden Faktor Φ erhalten. Wenden wir diese Regel auf die Zahl Φ selber an, dann muss von Anfang an der Faktor genau die Größe von Φ haben. Wie gesagt – Mathematiker-Logik! Also:
| 1,000000000000 | × | 1,618033988750 | = | 1,618033988750 |
| 1,618033988750 | × | 1,618033988750 | = | 2,618033988750 |
| 2,618033988750 | × | 1,618033988750 | = | 4,236067977500 |
| 4,236067977500 | × | 1,618033988750 | = | 6,854101966250 |
| 6,854101966250 | × | 1,618033988750 | = | 11,090169943749 |
| 11,090169943749 | × | 1,618033988750 | = | 17,944271909999 |
| 17,944271909999 | × | 1,618033988750 | = | 29,034441853749 |
| 29,034441853749 | × | 1,618033988750 | = | 46,978713763748 |
| 46,978713763748 | × | 1,618033988750 | = | 76,013155617496 |
| 76,013155617496 | × | 1,618033988750 | = | 122,991869381244 |
| 122,991869381244 | × | 1,618033988750 | = | 199,005024998740 |
| 199,005024998740 | × | 1,618033988750 | = | 321,996894379985 |
| 321,996894379985 | × | 1,618033988750 | = | 521,001919378725 |
| 521,001919378725 | × | 1,618033988750 | = | 842,998813758710 |
| 842,998813758710 | × | 1,618033988750 | = | 1364,000733137436 |
| 1364,000733137436 | × | 1,618033988750 | = | 2206,999546896146 |
| 2206,999546896146 | × | 1,618033988750 | = | 3571,000280033582 |
| 3571,000280033582 | × | 1,618033988750 | = | 5777,999826929728 |
| 5777,999826929728 | × | 1,618033988750 | = | 9349,000106963310 |
| 9349,000106963310 | × | 1,618033988750 | = | 15126,999933893039 |
«| Ja, das leuchtet mir ein ... vorher haben wir uns erst an diese ominöse Zahl immer weiter herangepirscht, aber jetzt haben wir gleich damit angefangen und sind sozusagen schon von Anfang an dort. Du hast recht, das ist »logisch«!
Wenn ich mir die »großen« Zahlen anschaue, dann werden diese offensichtlich immer mehr zu »ganzen Zahlen«. Denn 5777,9998269 ist fast genau 5778 und ebenso ist 9349,0001069 fast genau 9349. Kann man diese Folge nicht gleich von vornherein mit ganzen Zahlen beginnen?
|» Klar kann man das. Probier bitte Folgendes: Geh diese Folge von den großen ganzen Zahlen zu immer kleineren ganzen Zahlen durch und beobachte, was passiert.
«| O. k., ich beginne also bei 15126,99993389 – die gerundete ganze Zahl ist 15127 – und gehe zurück zu 9349 usw.:
| ⋮ |
| 2207 |
| 1364 |
| 843 |
| 521 |
| 322 |
| 199 |
| 123 |
| 76 |
| 47 |
| 29 |
| 18 |
| 11 |
| 7 |
| 4 |
| 3 |
| 1 |
Stimmt das so? Anstatt wie »von unten nach oben« immer die vorhergehende Zahl dazuzuzählen, ziehe ich jetzt »von oben nach unten« immer die letzte Zahl ab und schreibe das Ergebnis der Differenz hin.
|» Genau.
«| Gut, dann mache ich das jetzt weiter:
| ⋮ |
| 4 |
| 3 |
| 1 |
| 2 |
| −1 |
| 3 |
| −4 |
| 7 |
| −11 |
| 18 |
| −29 |
| ⋮ |
«| Das ist komisch. Die Zahlen werden wieder die gleichen, aber jetzt sind sie immer abwechselnd negativ und positiv! Hast du das gewusst?
|» Nicht, bevor ich es selber ausprobiert hatte. Ich war ebenfalls überrascht, als ich das gesehen hatte.
«| Ist das bei allen diesen Folgen so?
|» Diese Frage hatte ich mir auch gestellt, und da ich nicht sofort eine Antwort darauf fand, hab ich es einfach ausprobiert. Ich hab die mir bekannte Fibonacci-Folge genommen – die kennt man schon seit Jahrhunderten.
«| Aha. Und wie geht die?
|» Die beginnt mit 0 und 1.
«| Das probier ich gleich aus:
| 0 |
| 1 |
| 1 |
| 2 |
| 3 |
| 5 |
| 8 |
| 13 |
| 21 |
| 34 |
| 55 |
| 89 |
| 144 |
| 233 |
| ⋮ |
Kommt mir irgendwie bekannt vor ...
|» Kein Wunder, die steht in fast jedem Buch über Mathematik.
«| Aber wir wollten ja ausprobieren, ob die Folge nach »unten« auch wieder abwechselnd positive und negative Zahlen produziert ...
| ⋮ |
| 8 |
| 5 |
| 3 |
| 2 |
| 1 |
| 1 |
| 0 |
| 1 |
| −1 |
| 2 |
| −3 |
| 5 |
| −8 |
| 13 |
| −21 |
| ⋮ |
Sie tut es! Es schaut genau so aus wie bei dieser anderen Folge. Die gleichen Zahlen wie »oben«, nur eben abwechselnd positiv und negativ. Ich glaub, das ist wirklich bei allen diesen Folgen so. – Aber eines möchte ich jetzt noch probieren. Ich will dieses Φ dabei verwenden!
|» Gute Idee! Tu das.
«| Ich nehme Φ auf 3 Stellen nach dem Komma genau, das sollte reichen – es erspart mir allzu vieles Rechnen.
| ⋮ |
| 6,854 |
| 4,236 |
| 2,618 |
| 1,618 |
| 1,000 |
| 0,618 |
| 0,382 |
| 0,236 |
| 0,146 |
| 0,090 |
| 0,056 |
| 0,034 |
| 0,020 |
| 0,014 |
| ⋮ |
Da wird nichts negativ! Und außerdem geht das gegen 0, die Zahlen werden ja immer kleiner. Bei den ganzen Zahlen sind sie wieder größer geworden. Dort sind die gleichen Zahlen wieder zu sehen gewesen, nur dass sie eben abwechselnd positiv und negativ waren.
|» Rechne noch ein bisschen weiter ...
«| Meinst du? Ich sehe doch bereits, dass das gegen 0 geht! Aber bitte ...
| ⋮ |
| 0,020 |
| 0,014 |
| 0,006 |
| 0,008 |
| −0,002 |
| 0,010 |
| −0,012 |
| 0,024 |
| −0,036 |
| ⋮ |
Ah! So ist das! Ich glaube, das hängt damit zusammen, weil ich Φ auf nur 3 Stellen nach dem Komma hingeschrieben habe. Und als ich dann in die Gegend gekommen bin, wo so viele Nullen nach dem Komma waren wie die Genauigkeit meiner Rechnung, da ist die Folge aus der Spur gekippt.
|» Gut beobachtet! Es ist tatsächlich so. Je genauer du die Zahl Φ berechnest, desto länger dauert es, bis sie »aus der Spur kippt«, wie du es genannt hast. Wenn du eine Folge mit ganzen Zahlen berechnest, dann ist die Genauigkeit sozusagen 0 Stellen nach dem Komma und sie kippt tatsächlich ab dem Wert 0 aus der Spur. Nach „oben“ gerechnet kann so etwas nicht passieren, denn dort wird der Wert automatisch mit jedem Schritt genauer. Es ist wie bei einem Radfahrer, der sich nach vorne bewegt. Am Anfang schiebt er ein wenig an, und bei einer Geschwindigkeit knapp über 0 wackelt er noch ziemlich stark, das heißt, er muss ständig das Gleichgewicht ausgleichen, er fährt mal ein wenig nach links, dann wieder nach rechts, bis er schneller wird, und je schneller er fährt (je weiter er sich in der Folge „nach oben“ bewegt), desto kleiner müssen diese Korrekturen nach links oder rechts werden. Wenn er stillsteht, fällt er um – er kippt aus der Spur.
Die Folge, die genau mit Φ beginnt, ist sozusagen die Ideallinie für den Radfahrer. Die »Natur« der 3-dimensionalen Welt kennt jedoch nur ganze Zahlen. Etwas unendlich Genaues gibt es nicht. Selbst Licht besteht letztlich aus einzelnen, ganzen Licht-Quanten, den Photonen. Auch ein Lichtstrahl bewegt sich entlang einer schnurgeraden Ideallinie, allerdings so genau, dass wir die Abweichung nicht messen können – sie ist unmessbar gering.
Wenn wir die Größe des Idealwertes (Φ) herausfinden wollen, dann bleibt uns nichts Anderes übrig, als möglichst »weit zu wandern«, das heißt möglichst viele Stufen dieser Folge zu ersteigen und dann diese großen Zahlen, die wir dort finden, zu dividieren. Natürlich können wir auch einfach den Wert von Φ mit der Formel
| Φ | = |
|
möglichst genau berechnen. Aber auch das geht nur mit einer beschränkten Genauigkeit – diese Zahl lässt sich eben nicht exakt berechnen.
Ich zeige dir jetzt noch etwas, das du noch nicht sehen konntest, weil du zuletzt die Zahl Φ nur auf 3 Stellen nach dem Komma genau genommen hast. Berechne die Folge noch einmal, aber jetzt mit einer hohen Genauigkeit von 20 Stellen nach dem Komma.
«| Gut, ich bin schon gespannt, was du mir damit zeigen willst.
|
⋮
1.364,00073313743585740480 ⋮ |
|» Siehst du es? Die Zahlen, die kleiner als 1 sind, sind wieder genau die gleichen wie »oben«, allerdings ohne den ganzzahligen Teil – man sieht das aber nur bei jeder zweiten Zahl. Es ist der gleiche Effekt wie bei der Differenz zu den ganzen Zahlen. Mal ist der Wert etwas darüber, mal etwas darunter. Und alle Zahlen, die kleiner als 1 sind, sind nichts anderes als der Kehrwert zu den jeweiligen »oberen« Zahlen. Dadurch, dass man das gleiche Ergebnis auch bekommt, wenn man nach »oben« jeweils mit Φ multipliziert, bekommt man das Ergebnis nach »unten«, indem man durch Φ dividiert. Diese »Wachstumsformel« funktioniert also sowohl »von innen nach außen« als auch von »unten nach oben«. Es ist egal, ob man die Folge durch Addition gewinnt oder durch Multiplikation – sie ist identisch. Die Zahl ist »in sich selbst gespiegelt«. Sie wurde vor sehr langer Zeit auch Goldene Zahl genannt und ist heute unter dem Begriff Goldener Schnitt auch außerhalb der Mathematik bekannt. Aus meiner Sicht ist das Bemerkenswerteste die Tatsache, dass sie nicht genau berechenbar ist, dass auch bei noch so genauer Berechnung immer ein winziger Rest bleibt, den man noch genauer berechnen könnte. |
«| Kann man das irgendwie bildlich sichtbar machen?
|» Ja, das kann man. Nimm ein Rechteck mit den Seitenverhältnissen des Goldenen Schnitts, also eines, bei dem eine Seite 1 und die andere Seite Φ = 1,618034 lang ist.
Das sieht so aus:
 Bild 1
Bild 1
Anschließend zerschneidest du das Rechteck in einen Teil, der genau ein Quadrat mit der Seitenlänge 1 ist, und den Rest.
 Bild 2
Bild 2
Der »Rest« ist nun ebenfalls ein Rechteck mit genau dem gleichen Seitenverhältnis, nur eben kleiner. Du kannst dieses Rest-Rechteck wiederum in zwei Teile zerschneiden, wobei ein Teil genau ein Quadrat ist.
 Bild 3
Bild 3
Wieder bleibt ein Rest übrig, ebenfalls mit einem Seitenverhältnis von 1 : Φ. Der neue Rest wird ebenso in ein Quadrat und dessen Rest geteilt.
 Bild 4
Bild 4
Du siehst, man kann das beliebig oft machen:
 Bild 5
Bild 5
Als Ergebnis erhältst du ein Rechteck, das randvoll mit lauter Quadraten ist, die jeweils um den Faktor Φ kleiner sind. »Randvoll« ist nicht ganz richtig. Denn es bleibt immer ein winziger Rest übrig, den man nochmal unterteilen könnte ...
«| Ich habe jetzt ein wenig nachgegrübelt. Wenn ich mir diese winzigen Quadrate da ganz unten in der rechten Ecke anschauen möchte, dann brauche ich eine Lupe, um sie sehen zu können. Und wenn ich sie auf diese Weise vergrößert sehen kann, dann sieht alles genau so aus wie vorher, so wie die großen Quadrate. Da ist überhaupt kein Unterschied!
|» Ja, und das bleibt »in alle Ewigkeit« so. Es ändert sich nie etwas daran. Je mehr du es auch vergrößerst, es sieht immer gleich aus.
«| Ich brauche also gar nicht wirklich zu rechnen. Ich muss diese Quadrate lediglich verkleinern oder vergrößern, jetzt, wo ich weiß, dass das so ist.
|» Ja, aber Verkleinern oder Vergrößern ist etwas, das nicht durch Addition oder Subtraktion geschieht (also durch Dazu- oder Wegnehmen), sondern durch Multiplizieren oder Dividieren. Und wenn du es auf diese Weise machst, dann ist das nichts Anderes, als würdest du das Objekt einmal aus der Nähe und ein anderes Mal aus der Ferne betrachten. Du betrachtest jedoch immer ein und dasselbe Objekt. Anders ist es, wenn du tatsächlich etwas dazugibst oder wegnimmst. Dann ist das ein jeweils neues Objekt, das zwar gleich aussieht, aber nicht dieses selbe Objekt ist. Und noch etwas: Wenn du ein Objekt nur durch Vergrößern oder Verkleinern veränderst, so bleibt das Verhältnis seiner Abmessungen ebenfalls immer gleich. Du kannst nicht erkennen, ob die »Qualität«, die »Stimmigkeit« anders wird, denn das Objekt verändert sich ja überhaupt nicht. Wenn du aber jeweils das Ergebnis dessen, was du gerade getan hast, zum Ausgangspunkt des jeweils neuen Schrittes nimmst, den du machst, dann tritt tatsächlich eine Veränderung ein. Das Verhältnis der Objekte zueinander verändert sich, indem es sich der »Ideallinie« annähert. Ich nehme als Beispiel zwei unterschiedliche Quadrate und lege sie nebeneinander hin:
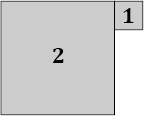 Bild 6
Bild 6
Du siehst sofort, dass das Verhältnis der Seitenlängen dieser beiden Quadrate zueinander keineswegs Φ entspricht. Wenn du oberhalb davon ein weiteres Quadrat dazulegst, das in seiner Seitenlänge der Summe der beiden Quadrate entspricht, und dann gleich links davon das Gleiche noch einmal machst, sieht das so aus:
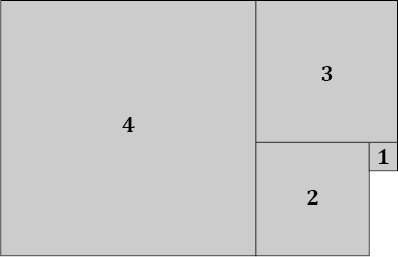 Bild 7
Bild 7
Man sieht auf einen Blick, dass das Verhältnis der beiden neuen Quadrate zueinander (Quadrat 4 zu Quadrat 3) bereits viel eher dem Wert von Φ entspricht. Wir haben hier nichts anderes getan, als unsere »Wachstumsregel« anzuwenden:
Nimm etwas und gib etwas Anderes dazu. Das Ergebnis ist etwas Neues.
Das machst du mit dem Anderen und dem Neuen wieder. Beliebig oft.
Nehmen wir ein weiteres Quadrat dazu:
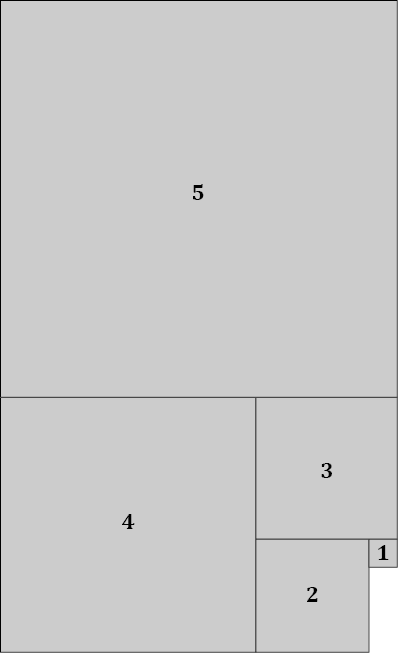 Bild 8
Bild 8
Die Seitenlängen der Quadrate 5 und 4 entsprechen in ihrem Verhältnis zueinander noch besser dem Wert von Φ als jene der Quadrate 4 und 3. Aber das kennst du ja nun schon ...
«| Weißt du, was mir auffällt? Durch Dazunehmen wird immer alles genauer, aber durch Wegnehmen kann ich das nicht erreichen. Durch oftmaliges Dazunehmen kann ich einen sehr genauen Wert von Φ erhalten. Beim »Zurückgehen«, also durch Wegnehmen, kann ich nur bis dorthin gehen, wo ich angefangen habe, ab dort wird es wieder ungenau ...
|» Ja, so ist das. Vorwärts geht es praktisch von alleine, dass du »in die Spur kommst«, zurück jedoch kippst du ab einem bestimmten Punkt unweigerlich heraus. Das »Werden« geschieht also immer nur in eine Richtung – nach »vorne« bzw. nach »oben«. Es ist wie mit der Zeit: Wenn du im Leben voranschreitest, dann nimmst du zu der Erfahrung, die du gerade gemacht hast, eine neue dazu, und das Ergebnis hat dich damit etwas genauer in deine Mitte gebracht. Die nächste Erfahrung, die auf den vorhergehenden aufbaut, bringt dich wieder ein wenig mehr in deine Mitte und so weiter ...
Zurückgehen kannst du jedoch nur bis zu jenem Punkt, von dem aus du begonnen hast – bis zu deiner »Geburt«. Davor war ja noch nichts ... Wenn du weiter zurückgehen willst, dann »spaltet es dich auf« (jeder Schritt wird abwechselnd Plus und Minus) und du siehst nur das, was du durch das Vorwärtsgehen ohnehin bereits kennst ...
Noch etwas fällt mir dazu ein: Die Genauigkeit, mit der du den Wert von Φ kennst, sagt etwas darüber aus, wie weit du zurückgehen kannst, bevor du »aus der Spur kippst«. Sie ist also ein direktes Maß deiner »Erfahrungen«, der Länge des Weges, den du zurückgelegt hast. Der gesamte Weg, den du gegangen bist, ist in dieser einen Zahl aufgezeichnet. Und zwar sowohl »innen« wie auch »außen« – also sowohl in den Nachkommastellen als auch im ganzzahligen Anteil. Und dabei ist es völlig egal, welchen Weg du genommen hast. Ob du von den Zahlen 17,3 und 3.889,2941 ausgegangen bist oder von den Zahlen −336,12 und 0,018997 – stets hast du dich der »Ideallinie« angenähert, aber du hast sie garantiert nicht exakt erreicht. Denk darüber nach!
Die Zahl Φ, so wie du sie kennst, der Wert, den du »errechnet« hast, also der genaue Wert des Verhältnisses der Zahlen, zu denen du nur auf diese eine Art und Weise gelangen konntest, indem du genau den Weg gegangen bist, den du genommen hast, enthält deinen gesamten Weg in sich. Sie ist die Aufzeichnung aller deiner »Erfahrungen«, die du gemacht hast. Und du kannst jederzeit von diesem Φ ausgehend beliebig weit diesen Weg zurückgehen, so weit, bis du zu deinem »Ursprung« gelangst, bis dorthin, von wo du ausgegangen bist. Weiter zurück gibt es nichts Neues zu finden.
Es gibt über diese Zahl Φ noch eine ganze Menge zu sagen. Darüber sind schon viele Bücher geschrieben worden. Sie ist seit Jahrtausenden bekannt und sehr viele alte Gebäude sind so gebaut worden, dass deren Proportionen dieser Zahl, dem »Goldenen Schnitt«, entsprechen.
Viele Formeln wurden entdeckt, deren Ergebnis die Zahl Φ bildet. Am schönsten finde ich die beiden folgenden:
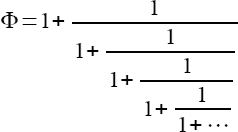
Die Formel hat die Form eines »unendlichen Kettenbruchs« und führte u. a. zu der mathematischen Erkenntnis, dass Φ die »irrationalste aller irrationalen Zahlen« sei.
Zum gleichen Ergebnis kommt eine »unendlich verschachtelte Wurzel«:
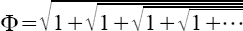
Ich überlasse es dir, die vielfältige Literatur dazu zu lesen und die darin enthaltenen Bilder zu bestaunen. Mein eigener Zugang zu den Zahlen war ein völlig anderer – ein spielerischer, ein ziemlich verrückter. Jener Radfahrer, der nie aus der Spur kippen wollte, und der daher immer in Bewegung bleiben wollte, der war ich. In noch jungen Jahren, während meiner Ausbildung zum Ingenieur der Elektrotechnik. Ich fuhr damals häufig in meiner Freizeit eine gut 10 km lange, stetig ansteigende Straße bergauf. Die Energie des jungen Mannes wollte sich austoben! Dabei kamen mir eine Menge Autos entgegen, die damals noch die alten österreichischen Kennzeichen trugen, welche nur aus einem Buchstaben und einer (meist) 6-stelligen Zahl bestanden. Es blieb nur wenig Zeit bis zum nächsten Auto, oft nur wenige Sekunden. Und während dieser kurzen Augenblicke versuchte ich aus den zufällig vorbeihuschenden Ziffern der Kennzeichen eine »gültige Formel« zu bilden, eine Gleichung. Erlaubt waren alle Rechenoperationen: Die Grundrechnungsarten Addition, Subtraktion, Division und Multiplikation sowie Potenzieren und Wurzelziehen. Außerdem durfte ich beliebige Vorzeichen (+ und −) verwenden. Auch Klammern waren erlaubt, allerdings kann ich mich nicht erinnern, je eine verwendet zu haben.
Drei Beispiele mögen illustrieren, welcher Narrheit ich damals während der anstrengenden Bergauffahrten (ich bin immer ziemlich schnell gefahren!) frönte:
Kennzeichen: N 154763
−1 + 5 = 4 = 7 − 6 + 3
Kennzeichen: O 521477
5⋅2⋅1 = −4 + 7 + 7
Kennzeichen: W 313823
3 + 13 = 8 + 23
Ich kann bis heute nicht sagen, warum mir dieses Spiel so viel Spaß gemacht hat. Es war einfach so – ein völlig harmloses Vergnügen. Und es »wurmte« mich, wenn ich mal keine Lösung fand oder die Zeit zwischen zwei Autos zu kurz war, um sie zu finden. Im Laufe der Zeit begegneten mir häufiger Autos, deren »Formel« ich bereits kannte. Ein kurzer Blick genügte, und ich wusste bereits, »wer das war«. Die Zahlen und ihre Gleichungen bekamen für mich eine Ähnlichkeit mit »Gesichtern«, die ich mir merken konnte, die ich auf einen Blick wiedererkennen konnte. Es war einfach »ein etwas anderer Blickwinkel auf die Welt«. Nicht mehr und nicht weniger. Ich empfinde Zahlen als überhaupt nichts Besonderes. Farben und Töne sind ja auch etwas Alltägliches. Eine Farbe entspricht einer bestimmten Wellenlänge oder Frequenz von Licht – eine Zahl pro Sekunde. Und ein Ton entspricht einer bestimmten Schwingungsfrequenz von Luft, dem Schall – einer Anzahl Schwingungen pro Sekunde. Schwingt die Luft schneller, ist der Ton »höher«, schwingt sie langsamer, ist er »niedriger«. Ist die Farbe »rot«, schwingt das Licht, über welches ich die Farbe sehe, langsam – seine Wellenlänge ist »lang«. Blau hat eine kürzere Wellenlänge und schwingt daher schneller. Es ist so banal, dass wir kaum jemals darüber nachdenken.
Zahlen sind »Hilfsmittel für unseren Verstand«. Die »Natur«, also »alles, was außerhalb von uns« ist, scheint mittels Zahlen besser verstehbar zu sein.
»Alles ist Zahl!« soll Pythagoras, einer der berühmtesten Mathematiker, gesagt haben. Ich füge dem ein Wort hinzu: »Alles ist auch Zahl!« So wie alles eine Farbe hat. Oder eine Temperatur. Oder eine Masse. Oder eine Form. ...
Unter allen Zahlen im Universum (so weit wir es bisher kennen), bildet genau eine genau die Mitte aller Zentren.
Indem wir weiter voranschreiten und dem gerade Hinzugefügten etwas Neues hinzufügen, nähern wir uns dieser Mitte. »Innen« und »außen« sind dabei immer gleich und dennoch sehr verschieden. Wie im Großen, so im Kleinen. Überall im Leben kannst du es sehen. Sogar in den Zahlen, von denen manche Menschen behaupten, sie wären bloß Erfindungen ...
